Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный горный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

BIS5_matem_org_ua

.pdf

Скачиваний:

Добавлен:

06.06.2015

Размер:

1.77 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 95 6 7 8 9 > Следующая >>>

Задача 54. Составить каноническое уравнение гиперболы, зная, что расстояние между фокусами 2c = 6 и эксцентриситет ε = 32 .

Решение. Так как c =3 , то из соотношения ac = 32 определяем a :

a = 2 c = 2

3 = 2 .

находим

b2 = c2 −a2 =9 − 4 =5

и каноническое

уравнение

гиперболы (26) будет:

−

=1.

Задача

55.

Составить

уравнение

гиперболы, фокусы которой

расположены на оси абсцисс,

симметрично относительно начала координат,

зная, что уравнения асимптот

y = ±

4 x

ти

те

и расстояние между фокусами 2c

= 20.

org

matem

Решение. Сравнивая данныей

уравнения с уравнениями (35), составляем

соотношение:

а=

дa

ф4

a2 .

Откуда b2 =а

Учитывая найденное выражение для b2

и то, что c2 =100

из формулы

(27) находим

a2 = c2 −b2 =100 −169 a2 .

Откуда

a2 (1 +169 ) =100

или

a2 =10025 9 = 90025 .

Тогда b2 =169 a2 =169 90025 =160025 ,

а искомое уравнение гиперболы согласно формуле (26) будет:

=1.

−

или

−

900

1600

Задача 56. Дана гипербола 16x2 −9 y2 =144 . Найти:

1) полуоси a и b ;

фокусы;

эксцентриситет;

уравнения асимптот;

уравнения директрис.

Решение: 1) приводим

к каноническому виду,

уравнение гиперболыГ

разделив обе части данного уравнения на 144;к

ти2

аy

−

=1.

те

org

Сравнивая полученное уравнение с.формулой (26), находим:

matem

2 =9 a =3;

=16 b = 4;

2) из формулые(27) имеем:

К2

= 25,c =5 .

+ a =16 +9

Следовательно,

F1(5;0) и F1(−5;0) – фокусы гиперболы;

3)ε = ac = 53 >1 – эксцентриситет гиперболы;

4)y = ± ba x = ± 43 x – уравнения асимптот гиперболы;

5)x = ±εa = ± 53 = ±95 – уравнения директрис гиперболы.

Задача 57. Найти расстояние фокусов

гиперболы

x2 −8 y2 =8 от

ее

асимптот.

Решение.

Запишем

каноническое

уравнение

данной

гиперболы

−

=1,

откуда

a =

8,b =1

–

полуоси

гиперболы,

поэтому согласно

формуле (35) уравнение асимптот будет

y = ±

или

8y = 0 .

c =3 ,

поэтому F1(3;0) и F2 (−3;0) –

Из формулы (27) находим, что

фокусы гиперболы. По формуле d =

Ax0 + By0 +C

находим расстояние фокуса

A2 + B2

F1(3;0)

8 y = 0

"фокуса

F2 (−3;0)

от асимптот

(или,

что то же самое,

от

асимптот):

| 3 ± 8 0 |

d =

=1.

1 +8

Задача 58. Установить,

что

ти

16x

−9 y

−64x −54 y −161

= 0

уравнениеа

те

определяет гиперболу. Найти ее центр и полуоси. Построить гиперболу.

org

matem

Решение. Выделим полныейквадраты относительно x и y .

16(x

−4x) −9( y

+6 yы) −161

= 0 ;

(

д)

(

)

−

+ 2

3y +9

−9

=161;

−2 2 x +р4

−

(x −2)2

(y +3)2 +81 =161;

−64ф−

(x −

=144 ;

−9(y +

(x −2)2

(y +3)2

=1.

−

Сравнивая это уравнение с формулой (36), приходим к выводу, что

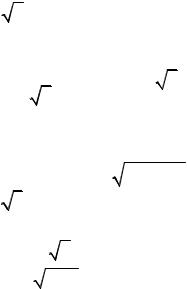
заданное уравнение определяет гиперболу с центром в точке O1 (2;−3) и

полуосями a =3 и b = 4 .

Построим гиперболу. Для этого в системе координат Oxy находим точку

O1 (2;−3), через которую проводим оси симметрии гиперболы (или, что тоже

самое, новые координатные оси O1X и O1Y ). В системе координат O1XY ,

так

же как и при построении эллипса (задача 38), сначала строим основной прямоугольник гиперболы по параметрам « a » и «b », затем через диагонали прямоугольника проводим прямые – асимптоты гиперболы, строим вершины

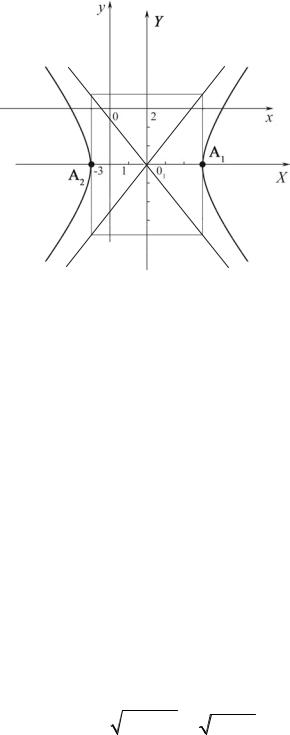
A1(3;0) и A2 (−3;0) и ветви гиперболы, пересекающие действительную ось в точках A1 и A2 и неограниченно приближающиеся к асимптотам (рис. 23).

Рис. 23

ти

Задача 59.

Убедившись,

M (−5; )

лежит

на гиперболе

что еочка

org

x2 y2

matem

радиусы точки M .

16 − 9 =1, определить фокальныее

M в уравнение, убеждаемся в

Решение. Подставляя координаты точки

том, что оно обращаетсярв тождество:

(

)

(−5)

−

(25

−9) =1 .

9 16

Значит точка M (−5;

9 ) лежит на гиперболе, причем на ее левой ветви, так

как абсцисса этой точки отрицательна.

Далее находим полуоси a = 4 и b =3 и эксцентриситет гиперболы

ε =

+b2

16 +9

а затем по формулам (21) вычисляем фокальные радиусы:

= −εx + a = −5 (−5) + 4 = 25 + 4 = 25 +16 = 41 =10 1 ;

= −εx − a = −5

(−5) − 4 = 25 − 4 = 9 = 2 1 .

Задача 60. Какие линии определяются следующими уравнениями:

1) y = + 2

x2 −9 ;

2) y = −3 x2 +1 ?

Изобразить эти линии на чертеже.

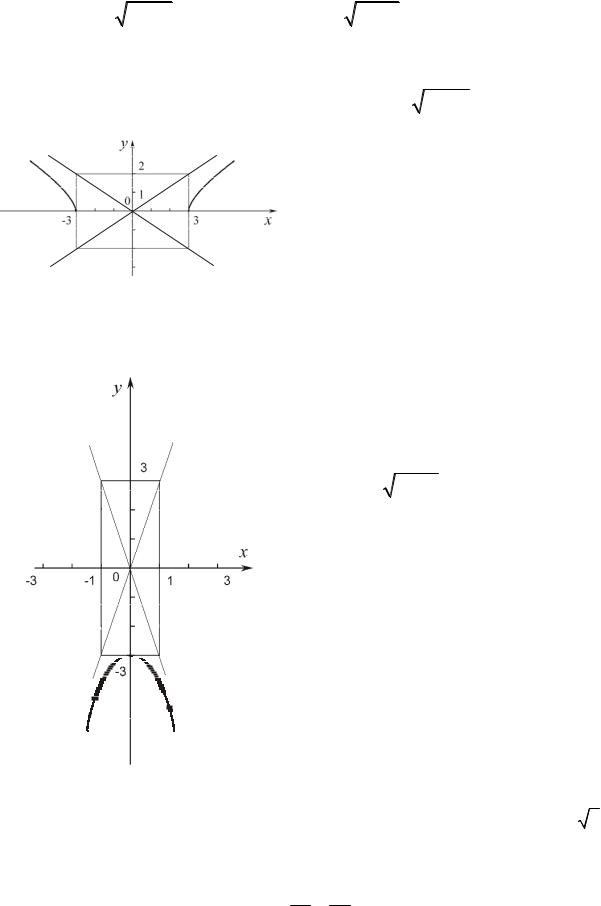
Решение: 1) запишем уравнение в виде

3 y =

x2 −9

и возведем его обе

части в квадрат:

= x

−9

или

x2 −

=9 .

После9 деления обеих частей

уравнения на 9, получим каноническое

уравнение гиперболыУ:

Рис. 24

−

4У

ординаты точек данной

Посколькук

линиитиположительны, то линия находится

в верхнейм

полуплоскости (рис. 24);

org

те

2) запишем уравнение в виде

matem

−

= x2

+1 .

Возводя его в квадрат, получаем:

= x2 +

1 или

−x2 +

–

a =1,

уравнение гиперболы с полуосями

b =3

и действительной осью Oy .

Поскольку ординаты точек гиперболы в

заданном уравнении отрицательны, то

ветвь гиперболы, определяемая заданным

уравнением,

находится

нижней

полуплоскости (рис. 25).

Рис. 25

Задача 61. Дана точка M1(10;

5) на

гиперболе

x2 − y2 =1. 80 20

Составить уравнение прямых, на которых лежат фокальные радиусы точки M1 .

Решение. Из данного канонического уравнения гиперболы имеем a2 =80 , b2 = 20 . Находим координаты фокусов гиперболы:

c = a2 +b2 = 80 + 20 =10 .

Следовательно, F1(10;0) и F2 (−10;0) – фокусы гиперболы. Далее составляем уравнения M1F1 и M1F2 , пользуясь уравнением прямой, проходящей через две точки:

y − 5

x −10

x −10 = 0;

0 −

y − 5

x −10

x −4 5y +З10

= 0.

−

−20

Задача 62.

ти

Составить уравнения касательных к гиперболе x2 − y2 =16 ,

проведенных из точки A(−1; −7) .

те

org

matem

Решение. Уравнение касат льных будем искать в виде y +7 = k(x +1) или

y = kx + (k −7) .

Далее решим совместнов

систему:

− y

=16 д x2 −[kx +(k −7)]2 =16

y = kx +(k

−7)

К2

− (k −7)

+16

= 0.

(1 −k ) −2k(k −7)x

При решении этого квадратного уравнения следует учесть, что его корни должны быть равными, так как прямая должна касаться кривой, т.е. кривая и прямая должны иметь одну общую точку. Это будет тогда, когда дискриминант квадратного уравнения окажется равным нулю.

Приравнивая дискриминант нулю, получим уравнение:

[2k(k −7)]2 +4(1 −k)2 (k −7)2 +16 = 0

k2 (k2 −14k +49) +(1 −k2 )(k2 −14k +65) = 0

k 4 −14 k 3 +49k2 +k2 −14k +65 − k 4 +14 k 3 −65k2 = 0

15k2 +14k −65 = 0

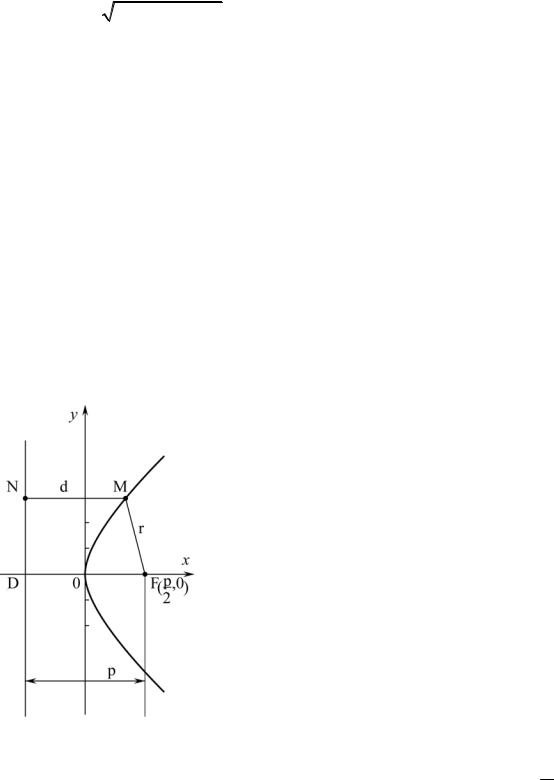
k	= −14 ±		196 +15 65 4 = −14 ± 64 ,
1,2			30	30

k =	5 , k	2	= −78 = −13 .
1	3		30	5

Запишем теперь уравнения касательных:

y+ 7 = 53 (x +1) 5x −3y −16 = 0

иy + 7 = −135 (x +1) 13x +5 y + 48 = 0 .

2.4. Парабола

Парабола –

геометрическое

место точек,

от

данной

равноотстоящих

точки, называемой фокусом, и данной прямой, называемой директрисой.

Если

за

ось

принять

фокуса на

перпендикуляр, опущенный из

директрису,

начало

координат

поместить

между фокусом и

посерединеУ

то

уравнение

директрисойГ

(рис. 26),

параболы

кбудет:

ти

= 2 px ,

(37)

где p = FD – параметр параболы.

те

.Фокальныйorg

радиус-вектор

любой

йточки параболы

matem

r = x +

(38)

директриса

данной

параболы

имеет

уравнение

x = −

(39)

Согласно определению параболы

(40)

где d = MN

Рис. 26

–

расстояние любой

точки

параболы от директрисы, равное x + 2p (38).

При указанном выборе системы координат парабола имеет ось симметрии параболы, называемую осью параболы, совмещенную с осью Ox , точку пересечения параболы с осью – вершину параболы, совмещенную с началом координат, т.е. вся парабола лежит в правой полуплоскости. Если же при аналогичном выборе системы координат парабола лежит в левой полуплоскости, то ее уравнение будет

y2 = −2 px .

(41)

В случае, когда начало координат находится в вершине параболы, а с ее осью совмещена ось ординат, парабола будет иметь уравнение

x2	= 2 py ,	(42)
если она лежит в верхней полуплоскости, и уравнение
x2	= −2 py ,	(43)

если в нижней.

Каждое из уравнений параболы (37), (41), (42), (43) называется

каноническим уравнением параболы.

Если вершина каждой из указанных парабол перенесена в точку O1(x0 ; y0 ) , то уравнения (37), (41), (42), (43) примут соответственно следующий вид:

( y − y

= 2 p(x − x

) ,

(44)

( y − y

= −2 p(x − x

) ,

(45)

(x − x )2 = 2 p( y − y ) ,

(46)

(x − x0 )

= −2 p( y − y0 ) .

(47)

, можно получить

Раскрывая квадраты разностей в указанных уравненияхЗ

уравнения второй степени вида (13), где

B = 0

A = 0 , либо C = 0 , т.е.

и либо

A C = 0 .

Таким образом, при

B = 0

ти

A C = 0 уравнение (13) может определять

параболу. При

этих же

значениях Aа, B,C

возможны также

случаи

ее

те

вырождения в

пару

параллельных

пару

совпавших прямых

или

( x

− a

= 0, a ≥ 0 ) в зависимости от значений.org D, E, F .

matem

Задача 63. Составитьыуравнение параболы, вершина которой находится в

начале

координат, знаяа, что парабола расположена в левой полуплоскости

оси Ox и ее параметр p = 0,5 .

симметрично относительнод

вид y

= −2 px ,

Решение. Уравнение искомой параболы

имеет

где

p = 0,5 , т.е. y2 = −x .

Задача 64. Определить величину параметра и расположение

относительно координатной оси параболы

y2 = 6x .

Решение. Сравнивая данное уравнение с каноническим уравнением параболы y2 = 2 px симметричной относительно оси Ox , находим

2 p = 6 p =3 .

Таким образом, величина параметра p равна 3 и поскольку при замене « y » на « −y » уравнение параболы не меняется, то парабола симметрична относительно оси Ox и лежит в правой полуплоскости.

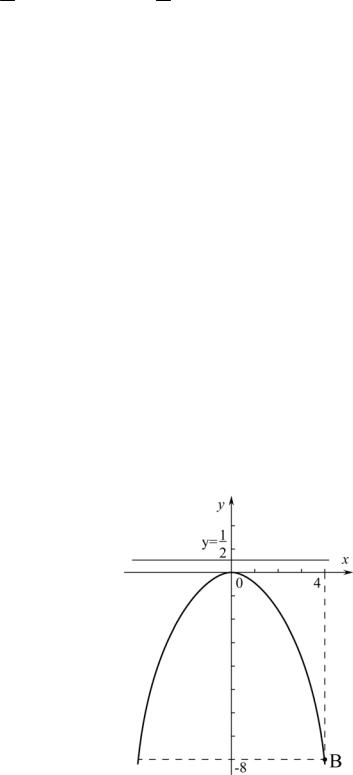
Задача 65. Составить уравнение параболы, которая имеет фокус F(0;−3) и проходит через начало координат, зная, что ее осью служит ось Oy .

Решение. Уравнение такой параболы имеет канонический вид x2 = −2 py ,

а фокус находится в точке F(0;− 2p ) . Из равенства − 2p = −3 находим p = 6 .

Следовательно, уравнение параболы будет x2 = −12 y .

Задача 66. Составить уравнение параболы, вершина которой находится в начале координат, зная, что парабола симметрично расположена относительно оси OX и проходит через точку A(9;6) .

Решение. Уравнение такой параболы будет

2 px .

Неизвестный параметр

найдем из

условия прохождения параболы

через точку A(9;6) . Подставляя в уравнение x =

9, yУ= 6 , получим

36 =

2 p 9 .

Откуда p = 2 и уравнение искомой параболы будет

ти

4x .

те

org

Задача 67. Составить уравненией

параболы с вершиной в начале координат,

симметрично расположенной относительно оси OY и проходящей через точку

B(4;−8) . Написать уравнение директрисы. Построить параболу и директрису.

matem

Решение.

каноническое

Используемр

= −2 py ,

так

как

уравнение параболые x

парабола

нижней

находитсяа

полуплоскости.

p параболы

Параметр

находим

из

условия ее

прохождения

через

точку

B(4;−8) :

16 = −2 p (−8) p = +1.

Следовательно, уравнение

искомой

параболы будет

x2 = −2 y ;

уравнение

директрисы

x =

т.е.

x =	1	(рис. 27).
	2	Рис. 27
		Рис. 27

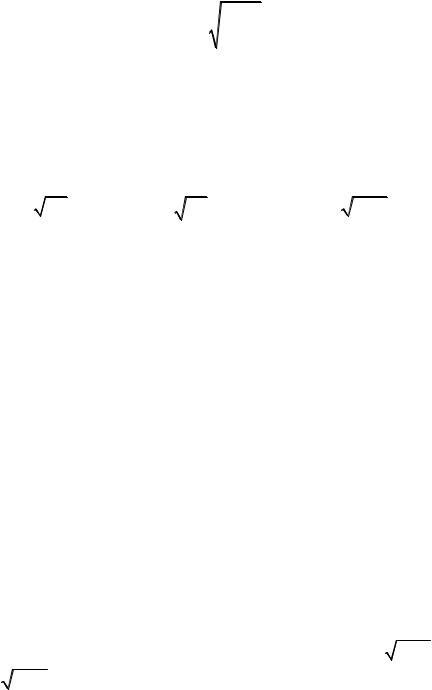
Задача 68. Исследовать взаимное расположение параболы y2 = x и прямой x + y − 2 = 0 .

Решение. Решаем систему уравнений:

y2 = x

= x

x + y −2

= 0

x = 2 − y

y2 + y −

2 = 0

= −

+2 = −

; y = −2, y

=1;

1,2

x = 2 − y

= 2 −

(−2) = 4; x

= 2 −1 =1.

Имеем точки (4;−2) и

(1;1) . Это означает, что прямая пересекает

параболу в точке M1(4;−2) и M2 (1;1) .

следующими

Задача 69. Установить, какие линии определяютсяГ

уравнениями:

"Н

1) y = + −x ;

2) x = −

3y ;

x −1 .

y =3 −4

Решение

≥ 0

или, что тоже, x ≤ 0 ; тогда

1. Данное уравнение определено, когдати−x

y ≥ 0

(2-я четверть системы координатмOxy ). Возводя обе части уравнения в

те

org

2 = −x ,

симметричной

квадрат, получаем каноническое уравнение параболы y

оси Ox .

На рисунке изображаем ту

относительно отрицательного направленияй

часть

параболы, которая

во

2-й

четверти

(рис. 28, а). Для

расположена

точкуmatem. Положим

построения зададим

еще

y = +2 ,

тогда

из

уравнения

одну

(−4;2) , через которую проходит парабола.

имеем: x = −4 , т.е. имеем точку

2. Это уравнениед определено, когда y ≥ 0 , но тогда из уравнения x ≤ 0

(2-я

четверть

координат

Oxy ).

Аналогично

предыдущему

системыф

уравнению

параболы x

=3y , симметричной

приходим к каноническому

относительно

оси

Oy .

Возьмем точку

на параболе. Для этого положим

x = −3 и из уравнения находим: y =

(−3)2

= 3.

Имеем точку M2 (3;3) , лежащую на параболе. Во 2-м координатном углу

строим точку M2 и проходящую через нее дугу параболы (рис. 28, б).

3. Аналогично предыдущему уравнение

y =3 −4

x −1 или,

что тоже,

y −3 = −4 x −1

определено,

когда

x ≥1

y ≤3,

т.е.

имеем

4-ю

четверть

новой системы координат O1XY с началом в точке O1(1;3) и осями O1X и O1Y , параллельными соответственно осям Ox и Oy . При этом, возводя обе части последнего уравнения в квадрат, получаем каноническое уравнение

<<< < Предыдущая 1 2 3 45 / 95 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.12.20193.32 Mб0bilet_20 (1).docx
#
18.09.201934.95 Кб1Bilet_vse_25.docx
#
24.04.20195.11 Mб3Bilyavskiy.doc
#
06.06.20151.34 Mб11BIS3_matem_org_ua.pdf
#
06.06.20151.4 Mб12BIS4_matem_org_ua.pdf
#
06.06.20151.77 Mб18BIS5_matem_org_ua.pdf
#
27.12.20192.33 Mб0Book2.doc
#
28.03.20162.42 Mб8book_full.pdf
#
15.11.2019564.21 Кб1Brif_dlya_konsultantov_ISTINNAYa_iyul_2012.docx
#
26.08.2019102.02 Кб2bukhuchet.docx
#
22.11.2019185.21 Кб2BYuDZhETUVANNYa_Rob_zoshit_dlya_studentiv.docx