Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный горный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

BIS5_matem_org_ua

.pdf

Скачиваний:

Добавлен:

06.06.2015

Размер:

1.77 Mб

Скачать

☆

1 / 91 2 3 4 5 6 7 8 9 > Следующая >>>

ти

org

matem

Министерство образования и науки Украины Национальный горный университет

Библиотека иностранного студента

Л.И. Бойко

А.М. Мильцын

В.И. Павлищев

МАТЕМАТИКА

ти

те

Частьм .org5

matem

ЭЛЕМЕНТЫАНАЛИТИЧЕСКОЙ

вГЕОМЕТРИИ

(в примерах и задачах)

Учебное пособие

Днепропетровск

НГУ

2008

УДК 514.12 (075.8) ББК 22.151.5я73 Б 77

Затверджено до видання навчально-методичним управлінням НГУ як навчальний посібник для студентів технічних спеціальностей різних форм навчання (протокол № 10 від 09.10.2007).

Бойко Л.Й., Мільцин А.М., Павліщев В.І.

Б 77 Математика. У 14 ч. Ч.5. Елементи аналітичної геометрії (у прикладах і

задачах): Навч. посібник. –Д.: Національний гірничий університет, 2008.

– 84 с. – Рос. мовою. – (Бібліотека іноземного студента).

рівня складності з

Посібник має близько 100 типових задач середньогоУ

. Орієнтований на

розв’язуванням, методичними вказівками та рекомендаціямиГ

організацію системної підготовки й самопідготовкик

Розглядаються пряма лінія на площиніти, криві другого порядку, площина,

те

пряма лінія у пространстві, а також на поверхнім

org

Для студентів – іноземних гром дян,

а також для студентів – громадян

України, що вчаться на всіх

очно, заочно, дистанційно, за

спеціальностяхм

matem

вечірньою формою та екстерноме.

100 типовых задач среднего уровня сложности с

Пособие содержитд

решениями, методическимиф

указаниями и рекомендациями. Ориентировано на

подготовки и самоподготовки.

организацию системнойК

Рассматриваются прямая линия на плоскости, кривые второго порядка, плоскость, прямая линия в пространстве и на поверхности.

Для студентов – иностранных граждан, а также для студентов – граждан Украины, обучающихся на всех специальностях очно, заочно, дистанционно, по вечерней форме и экстерном.

УДК 514.12 (075.8) ББК 22.151.5я73

Л.Й. Бойко, А.М. Мільцин, В.І. Павліщев, 2008

Національний гірничий університет, 2008

Содержание

Предисловие .........................................................................................................

1.ПРЯМАЯ НА ПЛОСКОСТИ .......................................................................

1.1.Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Уравнение прямой, проходящей через две точки ..............................................................................................

1.2.Уравнение прямой в отрезках.

Взаимное расположение двух прямых ............................................

2. КРИВЫЕ ВТОРОГО ПОРЯДКА ....................................................................

2.1. Общее уравнение кривой второго порядка. Окружность .................

2.2. Эллипс

2.3. Гипербола

..............................................................................................

2.4. Парабола

2.5. Полярные уравнения эллипса, гиперболы и параболы .....................

ти

3. ПЛОСКОСТЬ

те

4. ПРЯМАЯ В ПРОСТРАНСТВЕ

org

5. ПОВЕРХНОСТИ

matem

..............................................................................................

5.1. Цилиндрические поверхностиш

..............................................................

5.2. Поверхности .........................................................................вращенияы

5.3. Поверхности второго порядка.

Канонические .............................................дуравнения поверхностей

СПИСОК ЛИТЕРАТУРЫ ....................................................................................

ПРЕДИСЛОВИЕ

Учебное пособие подготовлено с целью повышения качества и прогнозирования результатов обучения иностранных студентов в областях знаний: разработка полезных ископаемых, информатика и вычислительная техника, машиностроение и металлообработка.

Соответствует проекту НГУ об издании серии «Библиотека иностранного студента», авторами которого являются профессора кафедры высшей математики Новикова Л.В. и Мильцын А.М., а также начальник управления международных связей профессор Рогоза М.В., декан горного факультета

профессор

Бузило

В.И. и

директор

ИЗДО

профессор

Рыбалко"

А.Я. Серия

к решению задач

содержит четырнадцать справочно-практических руководствГ

по математике.

"Н

Объем и содержание 5-й части «Элементы

Заналитической геометрии»

отвечает общему курсу высшей математики. Включает элементы теории,

задачи, методические указания к решению и, собственнои

, решение задач.

Работая

учебным

пособием,

научатся

распознавать

с удентыи

описывать

аналитически

различные

объекты,

именно:

геометрические

прямую линию, кривые второго порядкате

, плоскости и поверхности. Освоят

расположения, узнают условия

решение задач по определению взаимного.org

параллельности

перпендикулярностий

прямых,

плоскостей и

прямой

плоскостью. Научатся классифицировать поверхности и интерпретировать их

геометрически.

Получат

знания

по

алгебраическим

ыдополнительныеmatem

уравнениям первого и второго порядка.

Состав

подачи

материала

позволяет

планировать

структура

оперативно

общие и индивидуальные контрольные

тестовые

формировать

нагрузку и

самостоятельную

работу,

задания, распределять аудиторную

диагностировать усвоение учебного материала, вести контроль знаний и прогнозировать результаты.

Учебное пособие издано на русском языке, что обусловлено договором между университетом и иностранными студентами о языке их образования.

1.ПРЯМАЯ НА ПЛОСКОСТИ

1.1.Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Уравнение прямой, проходящей через две точки

Уравнение Ax + By +C = 0 ,

(1)

где А и В одновременно не равны нулю, называется общим уравнением прямой. Вектор n = ( A, B) , перпендикулярный к данной прямой, называется

нормальным.

Если С = 0, то прямая проходит через начало координат.

Если А = 0, то прямая параллельна оси ОХ. При В=0 прямая параллельна оси OY. Если А = С = 0, то получаем y = 0 – уравнение оси ОХ. При В = С = 0

имеем x = 0 – уравнение оси OY.

Уравнение прямой, записанное в виде

y = kx +b ,

(2)

называется уравнением прямой с угловым коэффициентом.

Здесь k = tgϕ ,

где

–

угол

прямой и положительным

между

ти

направлением оси ОХ.

, y

) в данном

Уравнение прямой, проходящейеч рез данную точку A(x

направлении (с заданным угловым

) записывается в виде

мкоэффициентом.org

) .

(3)

y − y ш= k(x − x

сA

matem

Его также называютауравнением пучка прямых.

Уравнения (2)

определяют любую прямую на плоскости кроме

ди (3)

одной, параллельнойфоси OY.

A(xA, yA ) и

УравнениеКпрямой, проходящей через две заданные точки

B( xB , yB ) , имеет вид

x − xA

y − yA

(4)

xB − xA

yB − yA

Задача 1. Построить прямую 3x −2 y +6 = 0 .

Решение. Для построения прямой достаточно знать какие-либо две ее точки, например, точки ее пересечения с осями координат. Точку А пересечения прямой с осью ОХ можно получить, если в уравнении прямой принять y = 0. Тогда имеем 3x +6 = 0 , т.е. x = −2 .

Таким образом, имеем точку A(−2;0) .

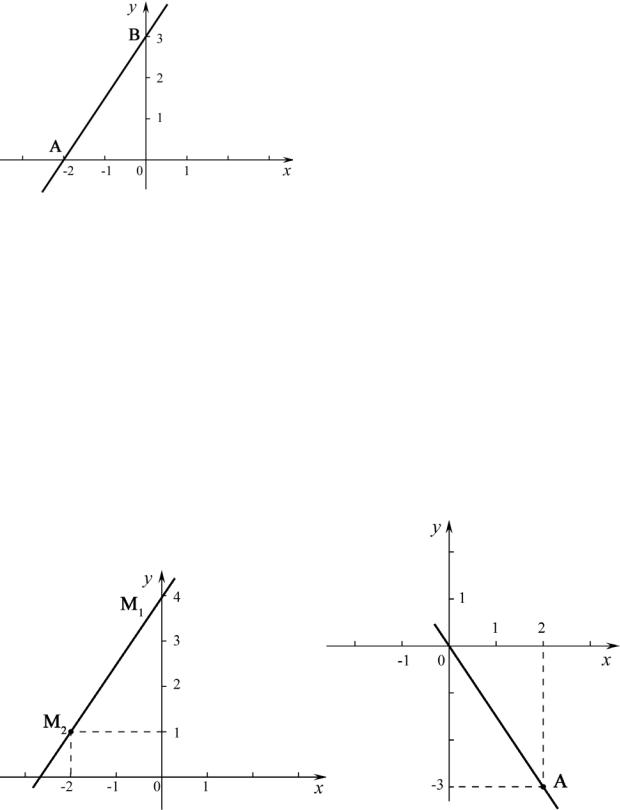
Точка В пересечения прямой с

осью ОY	имеет абсциссу x = 0 ;
следовательно, ордината точки		В
находится	из уравнения −2 y +6	= 0 ,

т.е. y = 3.

Таким образом, B(0;3) (рис. 1).

Рис. 1

3x −2 y +8 = 0 .

Задача 2. Построить прямую, определяемую уравнениемЗ

Решение. Запишем уравнение

в видек

y =

+4 .

возьмем,

ти

например, x1 = 0 и x2 = −2 , находим

=1. Через точки

M1(0;4) и

= 4

(−2;1)

org

проводим прямую (рис. 2). те

matem

Рис. 2

Рис. 3

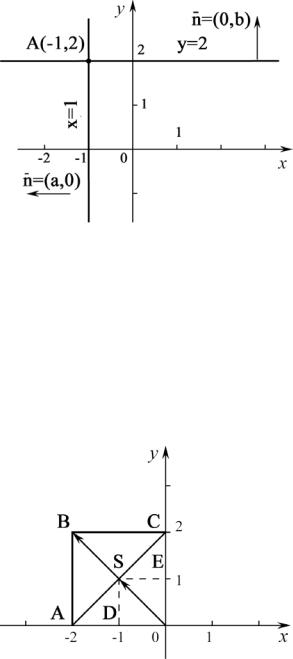
Задача 3. Построить прямую, определяемую уравнением 3x +2 y = 0 .

Решение. Так как в уравнении отсутствует свободный член, то прямая проходит через начало координат. Найдем еще одну точку. Полагая, например, x = 2 , находим y = −3. Проводим прямую через начало координат и точку А(2;-3) (рис. 3).

Задача 4. Написать уравнение прямых, проходящих через точку А(-1;2) параллельно координатным осям.

Решение. В общем уравнении прямой ax + by + c = 0 коэффициенты a

и b определяют координаты нормального

вектора к прямой:

n = (a,b) .

Если прямая параллельна оси ОХ, то

n = (0, b) .

Тогда

уравнение

прямой

−c

by + c = 0

или

y =

Учитывая,

ти

= c .

что прямая проходит через точку А(-1;2),

то уравнение ее y = 2 (рис. 4).

те

Аналогично

получаем

уравнением

org

matem

Рис. 4

прямой, проходящей

через

точку А,

параллельно оси Oy : x =1.

квадрата находится в начале, а точка пересечения

Задача 5. Одна из вершина

его диагоналей – в точкед S(−1;1) . Составить уравнение сторон квадрата.

Решение.

КВ квадрате диагонали делятся пополам точкой их пересечения

(рис. 5). Из равенства векторов

следуют равенства их проекций

OD = DA,

OE = EC.

A = −2,C = 2 .

Отсюда

следует

Тогда имеем уравнения сторон квадрата:

AO : y = 0; OC : x = 0; BC : y = 2; AB : x = −2.

Рис. 5

k = tgϕ =

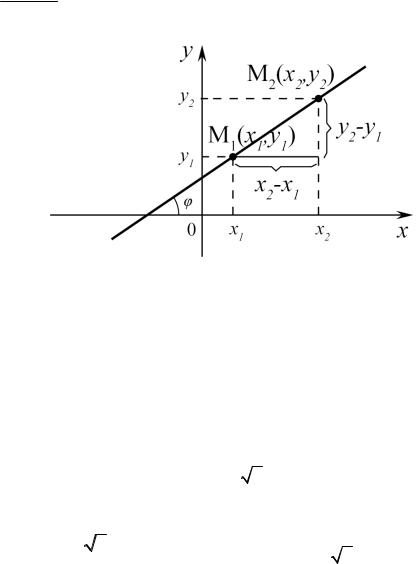
Задача 6. Даны две точки прямой. Найти ее угловой коэффициент.

Решение. Из рис. 6 очевидно решение. Оно дается формулой

y2 − y1 . x2 −x1

Рис. 6

ти

Задача 7. Составить уравнение прямойа , которая отсекает на отрицательной

те

с осью OX угол ϕ = 30 .

полуоси OY отрезок, равный 2 единицам, и образуетua

org

matem

прямой с угловым коэффициентом

Решение. Воспользуемся уравнениемй

(2): y = kx + b .

, b = −2 .

В нашем случае k = tgϕ = tg30

Имеем искомое уравнениед

yа=

x −2

или

3x −3y −6 = 0 .

Задача 8. Прямая, проходящая через точку A(−2;3) , образует с осью OX угол 135о. Составить уравнение этой прямой.

Решение. Угловой коэффициент прямой k = tg135D = −1. Уравнение прямой, проходящей через точку M0 ( x0 , y0 ) с угловым коэффициентом k имеет вид (3):

y − y0 = k( x −x0 ) .
В нашем случае
y −3 = −( x + 2)	или	x + y −1 = 0 .

Задача 9. Составить уравнение прямой, проходящей через точку A(−2;5) и образующей с осью OX угол 45о.

Решение. Угловой коэффициент	искомой	прямой k = tg45D =1.
Воспользовавшись уравнением прямой y − y0 = k( x −x0 ) , получаем
y −5 =1( x −(−2))	или	x − y + 7 = 0 .

Задача 10. Составить уравнение прямой, проходящей через точки A(−3;5)

и B(7;−2) .

Решение. Воспользовавшись уравнением

x −x1

y − y1

− x

− y

x −(−3)

y −5

x + 3

y −5

имеем

или

7 −(−3) −2 −5

−7

откуда 7x +10 y −29 = 0 .

Задача 11. Точка движется прямолинейно и в некоторые моменты времени

ти

имеет координаты (−6;1) и (−4;3) . Написать уравнение ее траектории.

те

Решение.

Точки

на

прямой. Используем

A(−6;1) и аB(−4;3)

лежат

org

y − y1

x − x1

уравнение прямой, проходящейеч рез две точки

Подставим

− y

− x

xmatem+ 6

−1

x + 6

y −ы1

координаты точек А и В:

или

или y = x + 7 .

а3−1

−4

+ 6

и C(6;5) . Составить

Задача 12. Даны вершины треугольника A(1;1), B(2;3)

уравнение медианы треугольника, проведенной из вершины А и найти ее длину.

Решение. Найдем координаты середины

D стороны ВС треугольника по

координатам концов:

+ x

2 + 6

+ y

3 +

xD =

= 4 ,

yD =

= 4

D(4;4) .

Искомое

уравнение медианы

находим по

формуле

x −xA

y − yA

xD −xA

yD − yA

x −1

y −1

откуда

или

y = x . Длину

находим по

формуле

4 −1

d = ( xD −xA )2 + ( yD − yA )2 . Имеем

d = AD = (4 −1)2 + ( y +1)2 = 2 32 = 3 2 .

1 / 91 2 3 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.12.20193.32 Mб0bilet_20 (1).docx
#
18.09.201934.95 Кб1Bilet_vse_25.docx
#
24.04.20195.11 Mб3Bilyavskiy.doc
#
06.06.20151.34 Mб11BIS3_matem_org_ua.pdf
#
06.06.20151.4 Mб12BIS4_matem_org_ua.pdf
#
06.06.20151.77 Mб18BIS5_matem_org_ua.pdf
#
27.12.20192.33 Mб0Book2.doc
#
28.03.20162.42 Mб8book_full.pdf
#
15.11.2019564.21 Кб1Brif_dlya_konsultantov_ISTINNAYa_iyul_2012.docx
#
26.08.2019102.02 Кб2bukhuchet.docx
#
22.11.2019185.21 Кб2BYuDZhETUVANNYa_Rob_zoshit_dlya_studentiv.docx