3. Результаты измерений

Таблица1. Среднее значение вылетов a-частиц за N опытов при заданном напряжении.

№	1	2	3	4	5	6	7	8	9	10	11
Напряжение блока питания ФЭУ	1000	1025	1050	1075	1100	1125	1150	1175	1200	1225	1250
Среднее значение вылетов a-частиц за N опытов	0	0	0	0	1	7	18	33	138	335	488
№	12	13	14	15	16	17	18	19	20	21
Напряжение блока питания ФЭУ	1275	1300	1325	1350	1375	1400	1425	1450	1475	1500
Среднее значение вылетов a-частиц за N опытов	569	612	622	629	636	641	648	648	660	708

2. Анализ результатов измерений

   1. Обработка результатов

Для определения рабочего напряжения ФЭУ задается количество измерений в выборке N, интервал времени счета Δτ. С помощью программы считается среднее значение вылетов -частиц за промежуток времени Δτ при установленном напряжении блока питания в диапазоне от 1000В до 1500В с шагом 50В. По полученным данным строится график зависимости x_ср от U. По графику определяется рабочее напряжение ФЭУ. В режиме непосредственного счета при оптимальном напряжении задается N=24 и Δτ=500мсек. Считается S_N, S_Xср при заданных параметрах. В режиме счет с выводом гистограммы задается N в диапазоне от 50 до 5000 и интервал времени счета Δτ в диапазоне от 1мсек до 100мсек. При данных N и Δτ строятся гистограммы с распределениями Гаусса и Пуассона.

2. Оценка погрешностей

Среднеквадратичное отклонение в режиме непосредственного счета σ=19.8.

σ определяется по формуле:

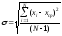
3. Обсуждение полученных результатов

При N∞ S_N стремится к постоянному пределу σ, который при нормальном распределении равен стандартному отклонению σ. При N∞ величина S_Xср стремится к нулю, а x_ср стремится к истинному значению µ. Распределение Пуассона является дискретной величиной, в отличие от распределения Гаусса, поэтому при малом количестве измерений Пуассон более точно описывает исследуемое явление, в отличие от Гаусса. При малом количестве измерений у Пуассона и Гаусса разные значения критерия ². Если количество измерений N устремить к бесконечности, то критерии ² у распределения Гаусса и Пуассона будут равны. Значения данных критериев будут близки к истинному значению. Вылет -частиц из источника является случайной величиной. Поэтому все полученные значения являются истинными, так как ошибки прибора так же носят случайный характер и этим сохраняется природа исследуемого явления. В этом заключается физический смысл эксперимента.

4. Выводы и заключение

Суть проделанной работы заключается в том, чтобы определить ² для разных распределений, и узнать интенсивность данного α-источника. Для этого производятся вычисления, определяются зависимости величин, анализируются графики зависимостей и гистограммы. Наш источник имел интенсивность 500 дел/сек. Оба распределения показывали ²>1 что говорит о том что гистограммы созданы с правильными параметрами, также это подтвердило что количество вылетов α-частиц величина постоянная.