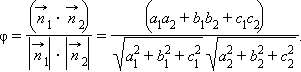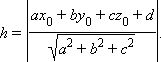13 Условия колинеарности,компл и ортогонал.

Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому вектору.

 Два ненулевых вектора иколлинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.

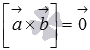или

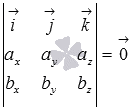
 Для коллинеарности необходимо чтобы их координаты были связаны соотношениями: или.или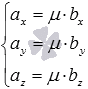

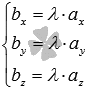
Векторы называются компланарными, если они принадлежат одной или параллельным плоскостям.

Для компланарности трех векторов итрехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.

Два ненулевых вектора называются перпендикулярными, если угол между ними равен девяноста градусам (радиан).

Для перпендикулярности двух ненулевых векторов инеобходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство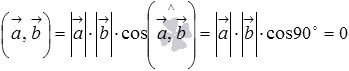

необходимое и достаточное условие перпендикулярности двух векторов в координатах имеет вид на плоскости, а в трехмерном пространстве.

14 Прямая линия на плоскости и ее уравнения

Прямая (прямая линия) - это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.

Уравнение прямой на плоскости

Любую прямую на плоскости можно задать уравнением прямой первой степени вида

A x + B y + C = 0

где A и B не могут быть одновременно равны нулю.

Уравнение прямой с угловым коэффициентом

Общее уравнение прямой при B≠0 можно привести к виду

y = k x + b

где k - угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ

Уравнение прямой в отрезках на осях

Если прямая пересекает оси OX и OY в точках с координатами (a, 0) и (0, b), то она может быть найдена используя формулу уравнения прямой в отрезках

x	+	y	= 1
a		b

Уравнение прямой, проходящей через две различные точки на плоскости

Если прямая проходит через две точки A(x₁, y₁) и B(x₂, y₂), такие что x₁ ≠ x₂ и y₁ ≠ y₂ то уравнение прямойможно найти, используя следующую формулу

x- x1	=	y- y1
x2 - x1		y2 - y1

Параметрическое уравнение прямой на плоскости

Параметрические уравнения прямой могут быть записаны следующим образом

	x = l t+ x0
	Y = m t+ y0

где (x₀, y₀) - координаты точки лежащей на прямой, {l, m}- координаты направляющего вектора прямой.

Каноническое уравнение прямой на плоскости

Если известны координаты точки A(x₀, y₀) лежащей на прямой и направляющего вектора n= {l; m}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу

x- x0	=	y - y0
l		m

15 Уравнение плоскости в Пространстве

Общее уравнение плоскости в декартовой системе координат записывается следующим образом: 

ax + by + cz + d = 0.

Если известно, что плоскость проходит через точку с координатами (x₀, y₀, z₀), то ее уравнение можно привести к виду 

a (x – x0) + b (y – y0) + c (z – z0) = 0.

Уравнение 

называется уравнением плоскости в отрезках на осях.

Нормаль к плоскости имеет координаты 

Угол между двумя плоскостями легко вычисляется по формуле скалярного произведения. Если эти плоскости задаются уравнениями a₁x + b₁y + c₁z + d₁ = 0 и a₂x + b₂y + c₂z + d₂ = 0, то угол между плоскостями равняется 

Расстояние от точки (x₀; y₀; z₀) до плоскости, задаваемой уравнением ax + by + cz + d = 0, равно 

16 Уравнение прямой в пространстве

• Векторное параметрическое уравнение прямой в пространстве:

где —радиус-вектор некоторой фиксированной точки лежащей на прямой,— ненулевойвектор, коллинеарный этой прямой (называемый её направляющим вектором), —радиус-вектор произвольной точки прямой.

• Параметрические уравнения прямой в пространстве:

где — координаты некоторой фиксированной точкилежащей на прямой;— координаты вектора, коллинеарного этой прямой.

• Каноническое уравнение прямой в пространстве:

где — координаты некоторой фиксированной точкилежащей на прямой;— координаты вектора, коллинеарного этой прямой.

• Общее векторное уравнение прямой^[в пространстве:

Поскольку прямая является пересечением двух различных непараллельных плоскостей, заданных соответственно общими уравнениями:

 и 

то уравнение прямой можно задать системой этих уравнений:

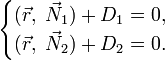
• Векторное уравнение прямой в пространстве

Уравнение прямой в пространстве можно записать в виде векторного произведения радиуса-вектора произвольной точки этой прямой на фиксированный направляющий вектор прямой:

где фиксированный вектор , ортогональный вектору, можно найти, подставляя в это уравнение радиус-вектор какой-нибудь одной известной точки прямой.