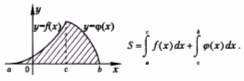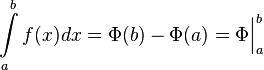39 Таблица основных интегралов

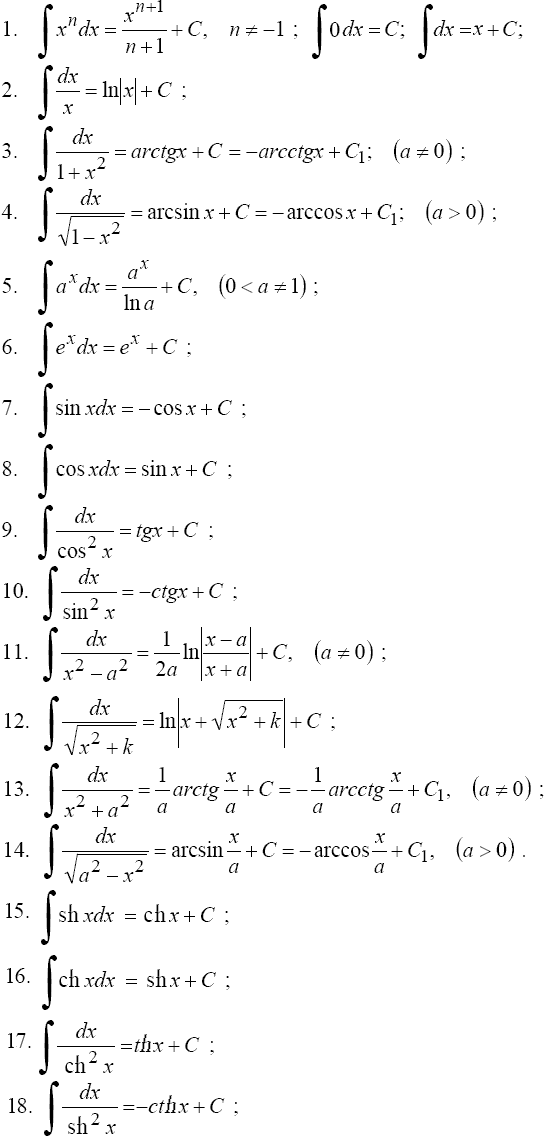
40 Метод непосредственного интегрирования

Определение

Метод интегрирования, при котором интеграл с помощью тождественных преобразований подынтегральной функции и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.

Таким образом, алгоритм действий следующий:

1. тождественное преобразование подынтегральной функции;

2. применение свойств неопределенного интеграла: вынесение константы за знак интеграла, представление интеграла от суммы функций в вид суммы интегралов;

3. использование таблицы интегралов.

41Интегрирование по частям и подставновкой

Интегрирование по частям. Если функции  u ( x )  и  v ( x ) имеют непрерывные первые производные и существует интеграл v ( x ) du ( x ), тосуществует и интеграл u ( x ) dv ( x ) и имеет место равенство:

 u ( x ) dv ( x ) = u ( x ) • v ( x ) – v ( x ) du ( x )

или в более короткой форме:

 u dv = u v – v du .

 

Обратите внимание, что интегрирование по частям и дифференциал произведения являются взаимно обратными операциями (проверьте!).

Интегрирование подстановкой (замена переменной). Если функция  f ( z ) определена и имеет первообразную при  z Z ,  а  функция  z = g ( x )имеет непрерывную производную при  x X  и её область значений  g ( X )  Z , то функция  F ( x ) =  f  [ g ( x )] × g' ( x ) имеет первообразную на  Х  и

 F ( x ) dx = f [ g ( x )] • g' ( x ) dx = f ( z ) dz .

42 Определен.Интеграл и его определение

Определённым интегралом от функции на отрезкеназывается предел интегральных сумм при стремлении ранга разбиения к нулю, если он существует независимо от разбиенияи выбора точек, то есть

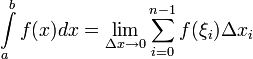
Если существует указанный предел, то функция называется интегрируемой напо Риману.

Основные свойства определенного интеграла

I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. , где х, t – любые буквы.

II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.

III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.

IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.

V. Постоянный множитель можно выносить за знак определенного интеграла.

VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.

43 Формула Ньютона — Лейбница

Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определённого интеграла и вычислением первообразной.

Если непрерывна на отрезкеи— её любая первообразная на этом отрезке, то имеет место равенство

44 Вычисление площадей с помощью интеграла.

1.Площадь фигуры, ограниченной графиком непрерывной отрицательной на промежутке [ a ; b ] функции f (x), осью Ох и прямыми х=а и х= b :

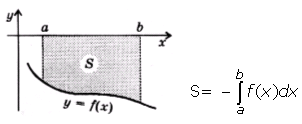
2.Площадь фигуры, ограниченной графиками непрерывных функций f (x), и прямыми х=а, х= b :

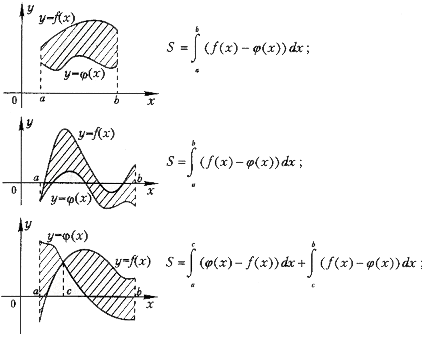
3.Площадь фигуры, ограниченной графиками непрерывных функций f (x) и :

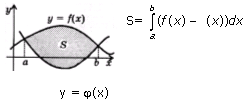
4.Площадь фигуры, ограниченной графиками непрерывных функций f (x), и осью Ох: