
- •1 Матрица
- •2 Определитель
- •3 Обратная матрица
- •4 Системы линейных алгебраических уравнений
- •5 Правило Крамера решения системы линейных уравнений
- •6 Метод гаусса решения системы линейных уравнений
- •7 Матричный метод
- •8 Декартова и полярная система координат
- •9 Векторы. Сложение и вычитание векторов. Умножение вектора на число.
- •10 Скалярное произведение векторов.
- •11 Векторное произведение векторов и его св-ва. Вычисление площадей
- •13 Условия колинеарности,компл и ортогонал.
- •14 Прямая линия на плоскости и ее уравнения
- •17 Кривые второго порядка, определения и канонические уравнения
- •18 Поверхности второго порядка
- •20 Свойствва пределов. Первый и второй замечтльный предел
- •21 Основные неопределенности пределов и их раскрытие.
- •22 Бесконечно малые и бесконечно большие функции
- •25 Непрерывность элементарных функций
- •28Физический смысл первой производной
- •29 Правила нахождения производная суммы разности произведения отношения функций
- •30 Таблица производных основных элементарных функций
- •31 Производ. Слож. Функц
- •32 Произв и диффер. Высш.Порядк
- •33 Монотон.Диффер.Высш.Функц.
- •34 Нахождение наибольшего и наименьшего значения функции на отрезке
- •35 Выпуклость функции, точки перегиба
- •36 Применение второй производной для нахождения интервалов выпуклости
- •37 Общая схема исследования функций
- •38 Первообраз и их множеств.
- •39 Таблица основных интегралов
- •40 Метод непосредственного интегрирования
- •41Интегрирование по частям и подставновкой
- •42 Определен.Интеграл и его определение
- •43 Формула Ньютона — Лейбница
- •44 Вычисление площадей с помощью интеграла.
- •45 Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной
- •47 Задача коши
35 Выпуклость функции, точки перегиба
График
функции ![]() ,
дифференцируемой на интервале
,
дифференцируемой на интервале![]() ,
является на этом интервалевыпуклым,
если график этой функции в пределах
интервала
,
является на этом интервалевыпуклым,
если график этой функции в пределах
интервала ![]() лежит
не выше любой своей касательной (рис.
1).
лежит
не выше любой своей касательной (рис.
1).
График
функции ![]() ,
дифференцируемой на интервале
,
дифференцируемой на интервале![]() ,
является на этом интервалевогнутым,
если график этой функции в пределах
интервала
,
является на этом интервалевогнутым,
если график этой функции в пределах
интервала ![]() лежит
не ниже любой своей касательной (рис.
2).
лежит
не ниже любой своей касательной (рис.
2).

Теорема
(Об условиях выпуклости или вогнутости графика функции)
Пусть
функция ![]() определена
на интервале
определена
на интервале![]() и
имеет непрерывную, не равную нулю в
точке
и
имеет непрерывную, не равную нулю в
точке![]() вторую
производную. Тогда, если
вторую
производную. Тогда, если![]() всюду
на интервале
всюду
на интервале![]() ,
то функция имеетвогнутость
на этом интервале,
если
,
то функция имеетвогнутость
на этом интервале,
если ![]() ,
то функция имеетвыпуклость.
,
то функция имеетвыпуклость.
Определение
Точкой
перегиба графика
функции ![]() называется
точка
называется
точка![]() ,
разделяющая промежутки выпуклости и
вогнутости.
,
разделяющая промежутки выпуклости и
вогнутости.
Теорема
(О необходимом условии существования точки перегиба)
Если
функция ![]() имеет
перегиб в точке
имеет
перегиб в точке![]() ,
то
,
то![]() или
не существует.
или
не существует.
Теорема
(О достаточном условии существования точки перегиба)
Если:
первая производная
 непрерывна
в окрестности точки
непрерывна
в окрестности точки  ;
;вторая производная
 или
не существует в точке
или
не существует в точке ;
; при
переходе через точку
при
переходе через точку  меняет
свой знак,
меняет
свой знак,
тогда
в точке ![]() функция
функция![]() имеет
перегиб.
имеет
перегиб.
36 Применение второй производной для нахождения интервалов выпуклости
Кривая ![]() называетсявыпуклой
вниз (вверх) в
промежутке
называетсявыпуклой
вниз (вверх) в
промежутке ![]() ,
если она лежит выше (ниже) касательной
в любой точке этого промежутка.
,
если она лежит выше (ниже) касательной
в любой точке этого промежутка.
Выпуклость
кривой, являющейся графиком функции ![]() ,
характеризуется знаком её второй
производной:если
в некотором промежутке
,
характеризуется знаком её второй
производной:если
в некотором промежутке ![]() ,
то кривая выпукла вниз в этом промежутке;
если же
,
то кривая выпукла вниз в этом промежутке;
если же![]() ,
то кривая выпукла вверх в этом промежутке.
,
то кривая выпукла вверх в этом промежутке.
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба.
Если
в точке перегиба x0 существует
вторая производная f
''( x0 ),
то ![]() .
.
Теорема.
Пусть ![]() дифференцируема
на промежутке
дифференцируема
на промежутке![]() .
Если во всех точках промежутка
.
Если во всех точках промежутка![]() вторая
производная функцииy=f(x) отрицательная,
т.е.
вторая
производная функцииy=f(x) отрицательная,
т.е. ![]() ,
то график функции на этом промежутке
выпуклый, если же
,
то график функции на этом промежутке
выпуклый, если же ![]() –
вогнутый.
–
вогнутый.
37 Общая схема исследования функций
и построения их графиков
При исследовании функций и построении их графиков целесообразно пользоваться следующей схемой.
1. Нахождение области определения функции.
2. Исследование функции на четность и нечетность.
3. Установление области непрерывности функции и точек разрыва. Отыскание вертикальных асимптот.
4. Исследование
поведения функции при ![]() (если
она там определена). Отыскание
горизонтальных и наклонных асимптот.
(если
она там определена). Отыскание
горизонтальных и наклонных асимптот.
5. Нахождение экстремумов и интервалов монотонности функции. Составление таблицы.
6. Нахождение интервалов выпуклости и вогнутости и точек перегиба графика функции.
7. Нахождение точек пересечения графика функции с осями, интервалов знакопостоянства функции. Составление таблицы. Отыскание дополнительных точек для построения графика.
8. Построение графика функции.
38 Первообраз и их множеств.
Первообразной
функции f(x) на
промежутке (a;
b) называется
такая функция F(x),
что выполняется равенство ![]() для
любогох из
заданного промежутка.
для
любогох из
заданного промежутка.
Множество всех первообразных
Если
принять во внимание тот факт, что
производная от константы С равна
нулю, то справедливо равенство ![]() .
Таким образом, функцияf(x) имеет
множество первообразных F(x)+C,
для произвольной константы С,
причем эти первообразные отличаются
друг от друга на произвольную постоянную
величину.
.
Таким образом, функцияf(x) имеет
множество первообразных F(x)+C,
для произвольной константы С,
причем эти первообразные отличаются
друг от друга на произвольную постоянную
величину.
Определение неопределенного интеграла.
Все
множество первообразных функции f(x) называется
неопределенным интегралом этой функции
и обозначается ![]()
свойства неопределенного интеграла
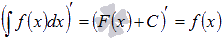 Производная
результата интегрирования равна
подынтегральной функции.
Производная
результата интегрирования равна
подынтегральной функции. Неопределенный
интеграл дифференциала функции равен
сумме самой функции и произвольной
константы.
Неопределенный
интеграл дифференциала функции равен
сумме самой функции и произвольной
константы. ,
где k –
произвольная константа.
Коэффициент
можно выносить за знак неопределенного
интеграла.
,
где k –
произвольная константа.
Коэффициент
можно выносить за знак неопределенного
интеграла. Неопределенный
интеграл суммы/разности функций равен
сумме/разности неопределенных интегралов
функций.
Неопределенный
интеграл суммы/разности функций равен
сумме/разности неопределенных интегралов
функций.
