6.2. Расчеты на прочность и жесткость стержней при кручении

Найденные значения касательных напряжений в произвольном сечении с абсциссой хпозволяют оценить прочность стержня, если известно допускаемое напряжения при кручении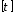для его материала. Условие прочности записывают в таком виде:

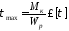. (6.11)

Поскольку 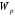выражается через диаметр сечения (формулы 6.6, 6.7), то из условия (6.11) можно найти либо требуемый диаметр вала (при заданном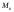), либо предельную величину крутящего момента (для заданного диаметра).

В некоторых случаях лимитирующим фактором работы стержня (детали) является обеспечение требуемой жесткости. Условие жесткости при кручении имеет вид:

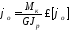, (6.12)

где 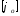- допускаемый относительный угол закручивания.

П р и м е р 6.1.

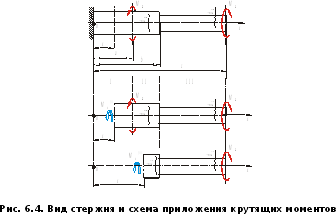
Построить по длине стального ступенчатого стержня (рис. 6.4) эпюры крутящих моментов и касательных напряжений, определить размер диаметра d₁ из условия прочности и жесткости и угол поворота торцевого сечения по отношению к сечению в заделке.

Исходные данные:

М₁ = 600 Н·м,М₂ = 900 Н·м,d₂ = 50 мм,а = 0,3 м, b = 0,5 м,с = 1,2 м.

Допускаемые напряжения для материала стержня на срез [] = 90 МПа, допускаемый угол закручивания [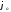] = 0,8 град/м, модуль упругости стали при сдвиге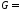8·10⁴МПа.

Р е ш е н и е.

Используем метод сечений. Разбиваем стержень на 3 участка (I,II,III). Искомый момент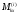в рассматриваемом сечении находим как сумму внешних моментов (с учетом знака), приложенных справа от рассматриваемого сечения.

Вначале рассмотрим участки стержня IиII, для которых задан диаметр (d₂).

Участок I():

Определяем крутящий момент как сумму внешних моментов, приложенных справа от произвольного сечения рассматриваемого участка.

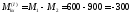Н·м.

Найдем величину полярного момента инерции сечения стержня

.

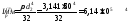Угол поворота сечения относительно заделки на участке Iс координатойx будет:

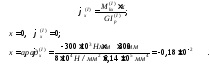
Участок II ():

Н·м.

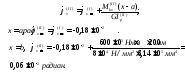
Для третьего участка вначале определяем крутящий момент и строим эпюру (рис. 6.5).

Участок III ():

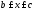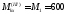Н·м.

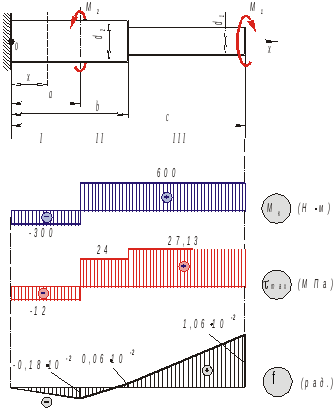
Рис. 6.5. Эпюры крутящих моментов, касательных напряжений

И углов поворота поперечных сечений

Определим требуемый диметр вала d₁ по двум условиям:

1. По условию прочности:

Используя условие прочности при кручении стержня круглого поперечного сечения (6.11) и выражение полярного момента сопротивления через диаметр вала (6.6), можно записать

,

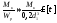откуда требуемый диаметр стержня будет

.

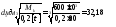2. По условию жесткости:

Поскольку вычисляемый погонный угол закручивания по формуле (6.12) получается в радианах, а допускаемый угол закрутки в условии задачи выражен в градусах, то определим допускаемую величину угла [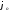] для единичной длины (1 мм), в радианах:

.

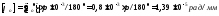Используя условие жесткости при кручении круглого вала единичной длины (6.12) и учитывая, что 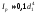, запишем:

.

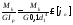Тогда, требуемый диаметр по условию жесткости будет

Из двух значений диаметра d₁ принимаем больший, округляя его до целой величины :d₁= 48 мм.

Полярный момент инерции поперечного сечения стержня на третьем участке будет

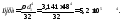
Угол поворота сечения с координатой x относительно заделки будет:

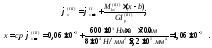
На рис. 6.5 изображена эпюра углов поворота поперечных сечений стержня из которой видно, что угол поворота торцевого сечения (x=c) по отношению к сечению в заделке составляет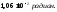

Поскольку теперь известны скручивающие моменты и диаметры стержня на всех участках, то определяем касательные напряжения на каждом из участков и строим эпюру касательных напряжений условно принимая знаки для касательных напряжений такими же, как и знаки крутящих моментов.

Участок I():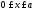

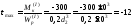МПа.

Участок II ():

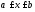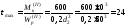МПа.

Участок III ():

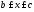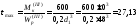МПа.

На рис. 6.5 изображена эпюра касательных напряжений по длине стержня.