
- •Конспект лекцій з курсу лінійної алгебри та аналітичної геометрії
- •§9. Лінії другого порядку 106
- •Організація навчального процесу за кредитно-модульною системою
- •§1. Матриці
- •1.1. Основні поняття
- •1.2. Дії над матрицями
- •1.3. Транспонування матриць
- •§2. Визначники
- •2.1. Основні поняття
- •2.2. Властивості визначників
- •§3. Невироджені матриці
- •3.1. Основні поняття
- •3.2. Обернена матриця
- •3.3. Ранг матриці
- •§4. Системи лінійних рівнянь
- •4.1. Основні поняття
- •4.2. Розв’язання невироджених лінійних систем
- •4.3. Розв’язання довільних лінійних систем. Теорема Кронекера-Капеллі
- •4.4. Розв’язання лінійних систем методом Гауса
- •§5. Вектори
- •5.1. Основні поняття
- •5.2. Лінійні операції над векторами
- •5.3. Розклад вектора за базисом
- •5.4. Лінійні операції над векторами в координатній формі
- •5.5. Декартова прямокутна система координат
- •5.6. Поділ відрізка в даному відношенні
- •§6. Добутки векторів
- •6.1. Скалярний добуток векторів
- •6.2. Векторний добуток векторів
- •6.3. Мішаний добуток векторів
- •§7. Лінії на площині, поверхні і лінії в просторі
- •7.1. Рівняння лінії на площині
- •7.2. Рівняння поверхні та лінії в просторі
- •§8. Площина, пряма в просторі і на площині
- •8.1. Загальне рівняння площини
- •8.2. Загальне рівняння прямої на площині
- •8.3. Канонічні і параметричні рівняння прямої. Рівняння прямої з кутовим коефіцієнтом
- •8.4. Загальні рівняння прямої в просторі
- •8.5. Рівняння прямої, що проходить через дві точки
- •8.6. Рівняння площини, що проходить через три точки
- •8.7. Кут між площинами, кут між прямими, кут між прямою і площиною
- •8.8. Відстань від точки до площини і від точки до прямої на площині
- •8.9. Умова, при якій дві прямі лежать в одній площині
- •Пряма на площині
- •Площина
- •Пряма в просторі. Пряма і площина
- •§9. Лінії другого порядку
- •9.2. Гіпербола
- •9.3. Парабола
- •9.4. Еліпс, гіпербола, парабола з осями, паралельними осям координат
- •Відповіді
- •Індивідуальні завдання
- •Тестові завдання з лінійної алгебри
- •Відповіді
- •Тестові завдання з аналітичної геометрії
- •Відповіді
1.2. Дії над матрицями
Додавання. Дія додавання матриць вводиться тільки для матриць однакових розмірів.
Сумою
двох матриць
![]() і
і
![]() називається матриця
називається матриця
![]() така, що
така, що
![]() ,
де
.
,
де
.
Сума
трьох матриць
![]() – це матриця, яка отримується послідовним
додаванням даних матриць, тобто
– це матриця, яка отримується послідовним
додаванням даних матриць, тобто
![]() .
.
Аналогічно
визначається
![]() для
для
![]() .
.
Приклад
1.1.
Знайти
суму
![]() ,
якщо
,
якщо
![]() .
.
Розв’язок.
![]() .
.
Множення
матриці на число. Добутком
матриці
на число
![]() (або числа
на матрицю
(або числа
на матрицю
![]() )
називається матриця
)
називається матриця
![]() така, що
така, що
![]() .
.
Добуток
матриці
![]() на число
позначається
на число
позначається
![]() або
або
![]() .
.
Приклад 1.2. Знайти добуток матриці
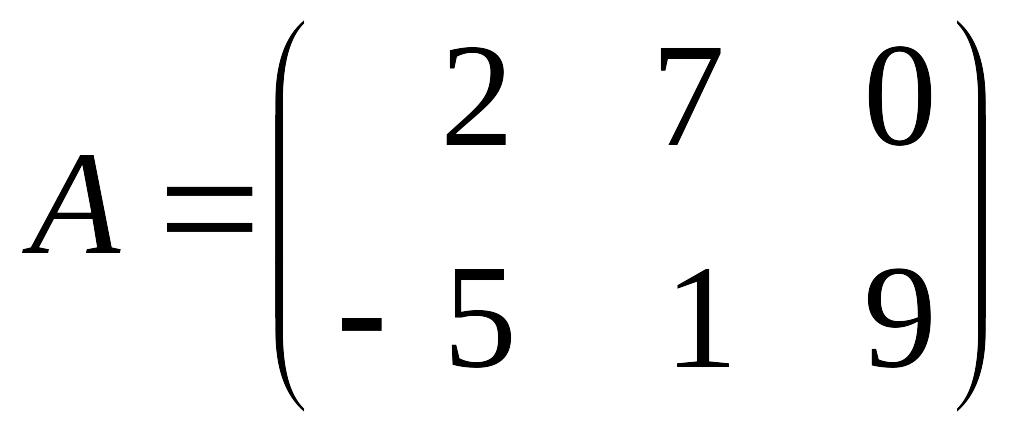
на число
![]() .
.
Розв’язок.
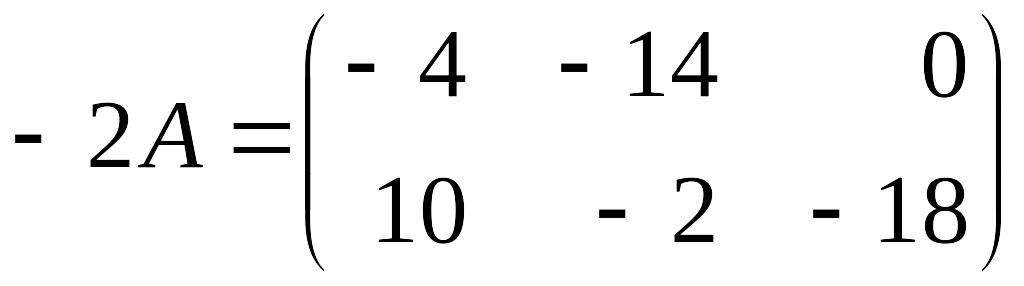 .
.
Матриця
![]() називається протилежною
до матриці
.
називається протилежною
до матриці
.
Різницю
матриць
![]() можна визначити як
можна визначити як
![]() .
.
Операції додавання матриць і множення матриці на число називають лінійними операціями над матрицями і мають наступні властивості:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]() ;
;
5.
![]() ;
;
6.
![]() ;
;
7.
![]() ;
;
8.
![]() ,
,
де А,
В, С,
О
–
матриці,
![]() – числа.
– числа.
Множення матриць. Операція множення двох матриць вводиться тільки для випадку, коли число стовпців першої матриці рівне числу рядків другої матриці. Такі матриці називаються узгодженими.
Добутком
матриці
на матрицю
![]() називається
матриця
називається
матриця
![]() така, що
така, що
![]() ,
де
,
де
![]() ,
тобто елемент і-го
рядка і
,
тобто елемент і-го
рядка і
![]() -го
стовпчика матриці
-го
стовпчика матриці
![]() дорівнює сумі добутків елементів і-го
рядка матриці
на відповідні елементи
-го
стовпчика матриці
дорівнює сумі добутків елементів і-го
рядка матриці
на відповідні елементи
-го
стовпчика матриці
![]() .
.
Приклад
1.3.
Знайти
добуток
![]() ,
якщо
,
якщо
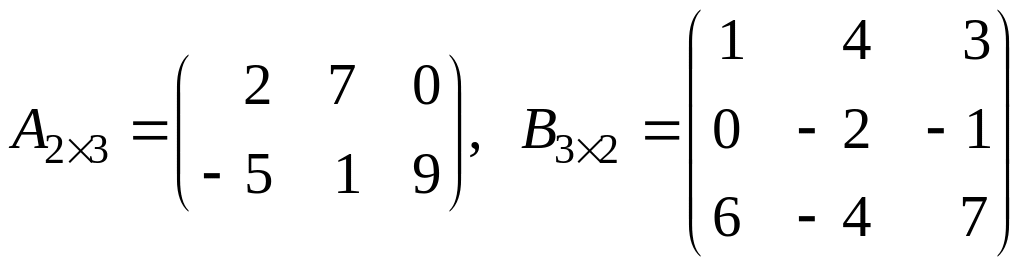 .
.
Розв’язок.
![]()
![]() .
.
Якщо А
і В
квадратні
матриці одного порядку, то добутки АВ
і
ВА
завжди
існують. Якщо
![]() ,
то матриці А
і
В
називаються
перестановочними.
,
то матриці А
і
В
називаються
перестановочними.
Якщо
матриця
узгоджена з матрицею
,
а матриця
узгоджена з матрицею
,
то під добутком
![]() трьох матриць розуміємо матрицю, отриману
послідовним множенням даних матриць,
тобто –
трьох матриць розуміємо матрицю, отриману
послідовним множенням даних матриць,
тобто –
![]() .
.
Операція множення матриць має властивості:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]() ;
;
5.
![]() ;
;
6.
![]() ,
,
де А,
В,
С
– матриці,
![]() – одинична та нульова матриці відповідно,
– число.
– одинична та нульова матриці відповідно,
– число.
Елементарні перетворення матриць. Елементарними перетвореннями матриць є наступні перетворення:
1) множення деякого рядка або стовпця матриці на число відмінне від нуля;
2) додавання до одного рядка або стовпця матриці іншого рядка або стовпця, помноженого на довільне число;
3) перестановка місцями двох рядків або стовпців матриці.
Дві
матриці
і
називаються еквівалентними,
якщо одна з них отримується з іншої за
допомогою елементарних перетворень і
позначаються
![]() .
.
1.3. Транспонування матриць
Матриця, отримана з даної заміною кожного її рядка (стовпчика) стовпчиком (рядком) з тим же номером, називається транспонованою до даної.
Матрицю,
транспоновану до матриці
,
позначають
![]() .
.
Операція знаходження матриці, транспонованої до даної, називається транспонуванням матриці.
Якщо
– матриця розмірів
![]() ,
то
має розміри
,
то
має розміри
![]() .
.
Справедливі наступні властивості:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ,
де
і
– матриці однакових розмірів;
,
де
і
– матриці однакових розмірів;
4.
![]() ,
де матриця
узгоджена з матрицею
.
,
де матриця
узгоджена з матрицею
.
Приклад 1.4. Знайти матрицю, транспоновану до матриці
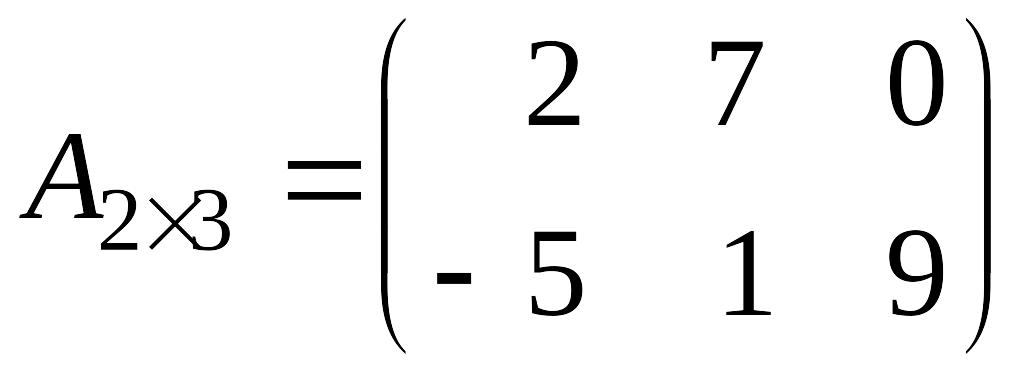 .
.
Розв’язок.
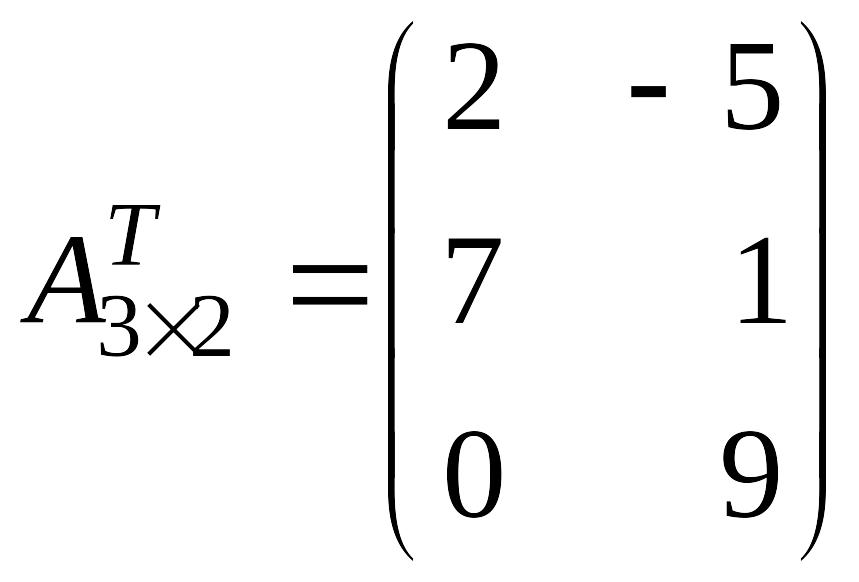 .
.
Теоретичні питання
Що називається матрицею розмірів
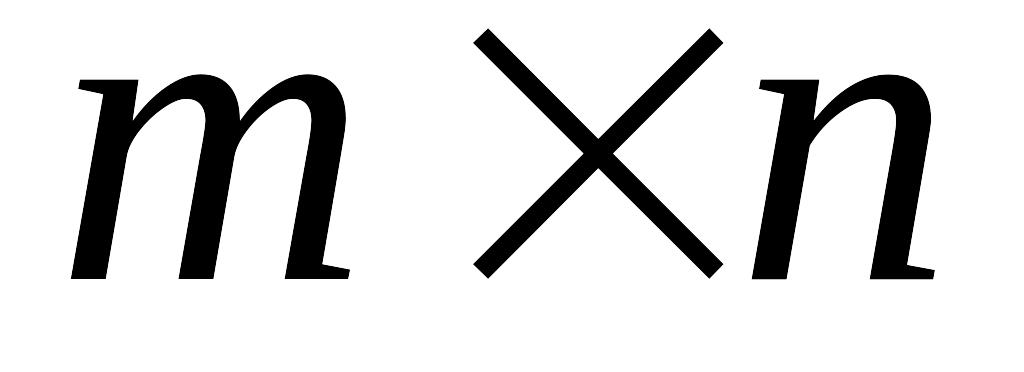 ?
?Які матриці називаються рівними?
Яка матриця називається квадратною?
Яка матриця називається діагональною?
Яка матриця називається одиничною?
Яка матриця називається трикутною?
Яка матриця називається трапецієвидною?
Яка матриця називається нульовою?
Які дії над матрицями називаються лінійними?
Які властивості лінійних операцій над матрицями?
Які матриці називаються узгодженими?
Що називається добутком матриці А на матрицю В?
Які властивості добутку матриць?
Які перетворення матриць називають елементарними?
Яка матриця називається транспонованою до даної?
Які властивості має операція транспонування матриці?
Задачі та вправи
Вказати розміри матриць:
а)
 ;
б)
;
б)
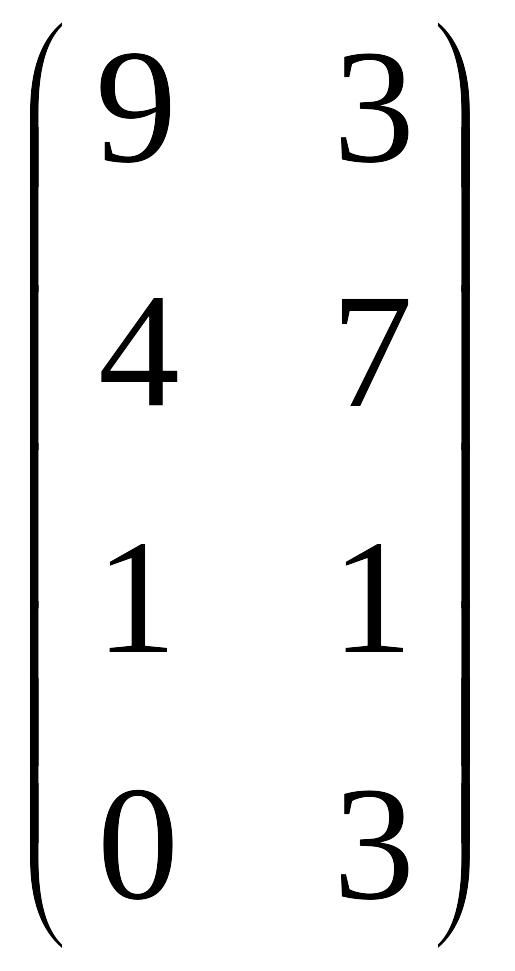 ;
в)
;
в)
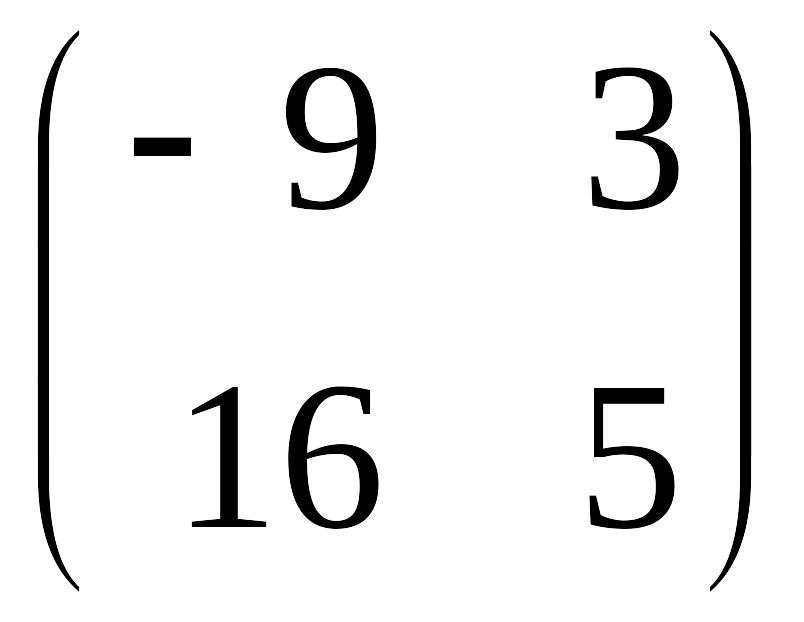 ;
г)
;
г)
![]() .
.
1.2.
Чому рівні в матриці А елементи
![]() ,
якщо
,
якщо
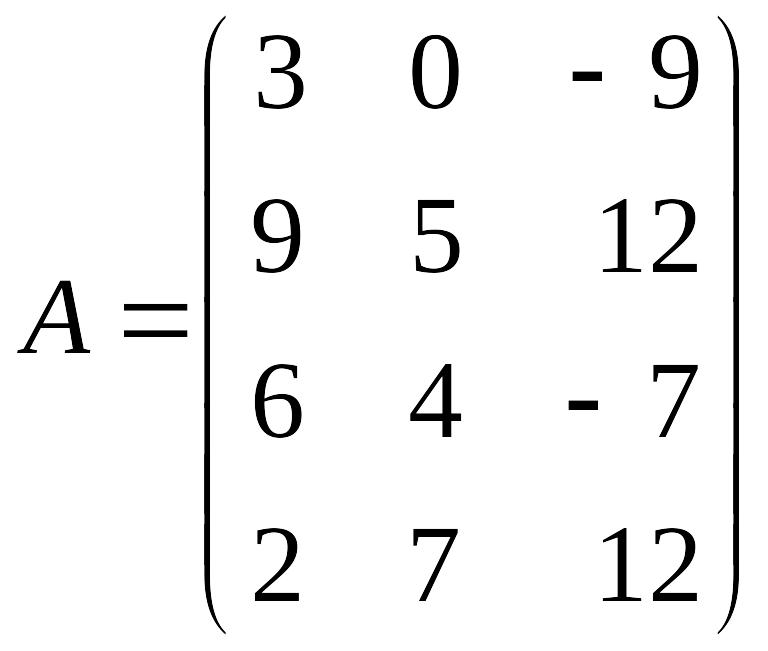 ?
?
Вказати, які з матриць
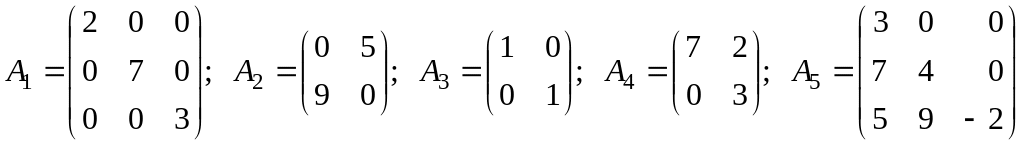 ;
;
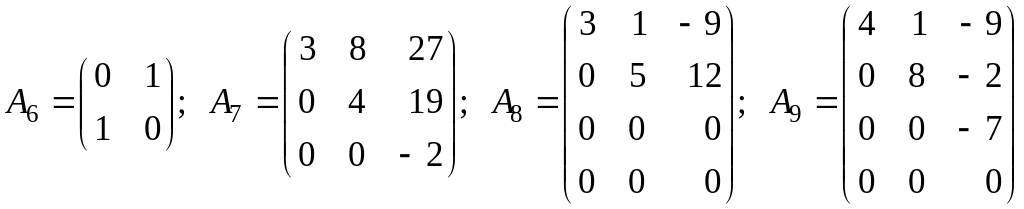
є: а) діагональними; б) одиничними; в) трикутними; г) трапецієвидними?
1.4. Знайти матрицю Х, якщо
а)
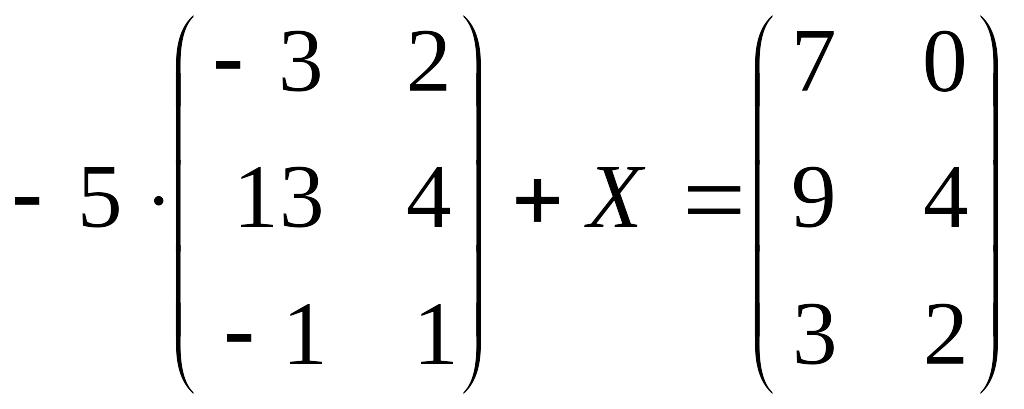 ;
б)
;
б)
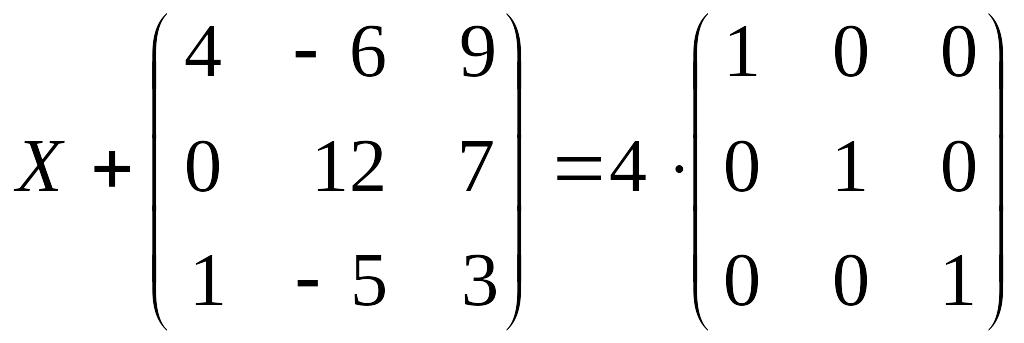 .
.
1.5. Знайти:
![]() ,
,
де
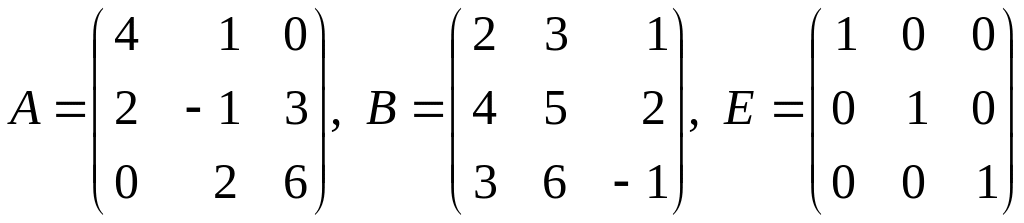 .
.
Розв’язок. Обчислення розіб’ємо на окремі дії:
1)
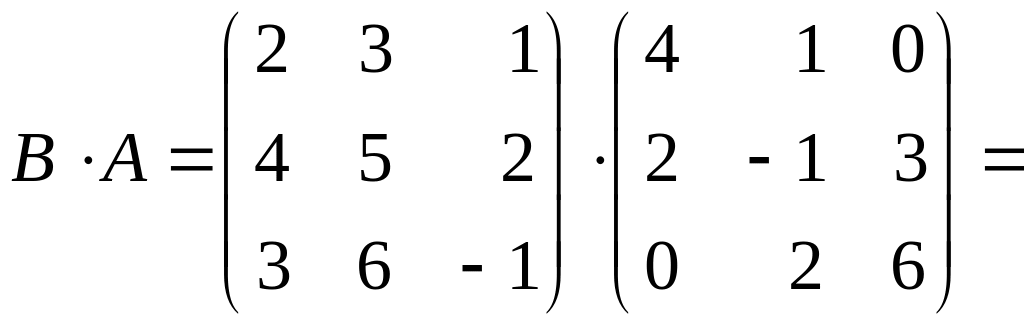
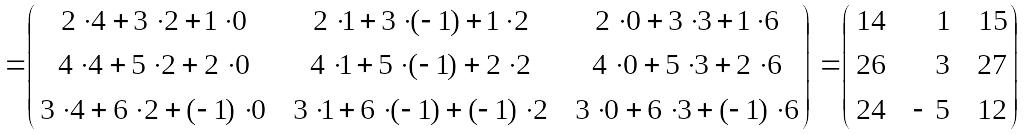 ;
;
2)
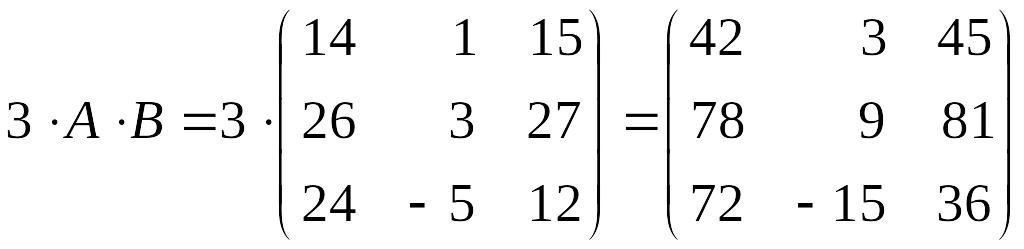 ;
;
3)
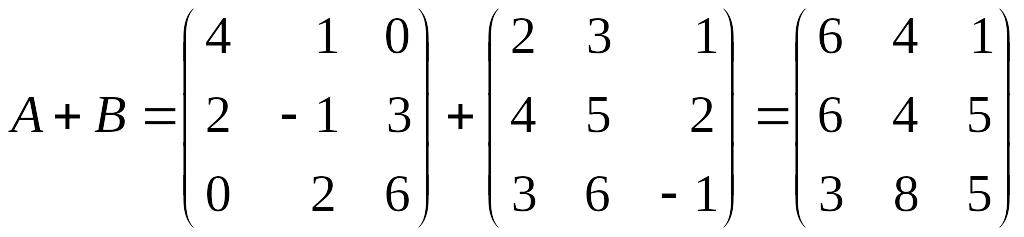 ;
;
4)
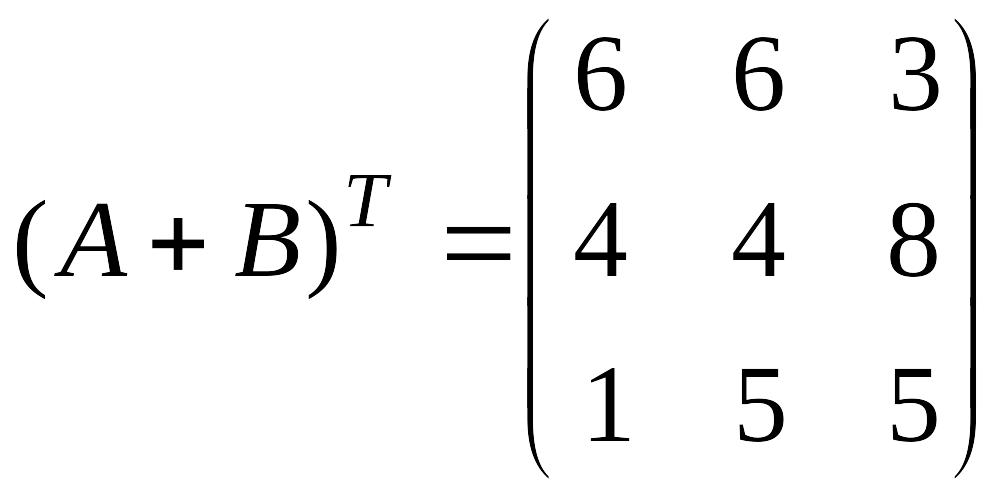 ;
;
5)
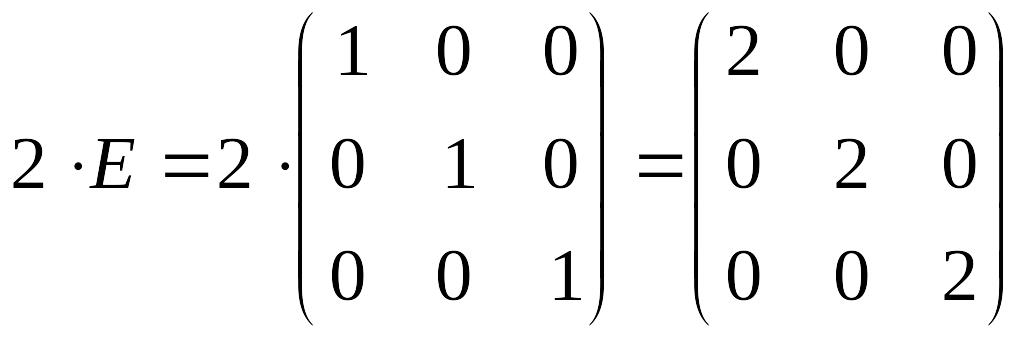 ;
;
6)
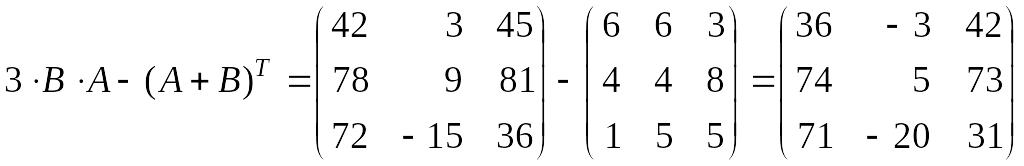 ;
;
7)
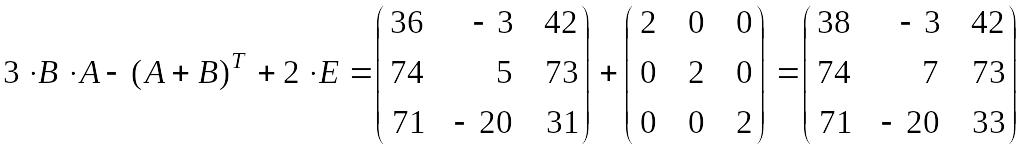 .
.
1.6. Знайти добуток матриць:
а)
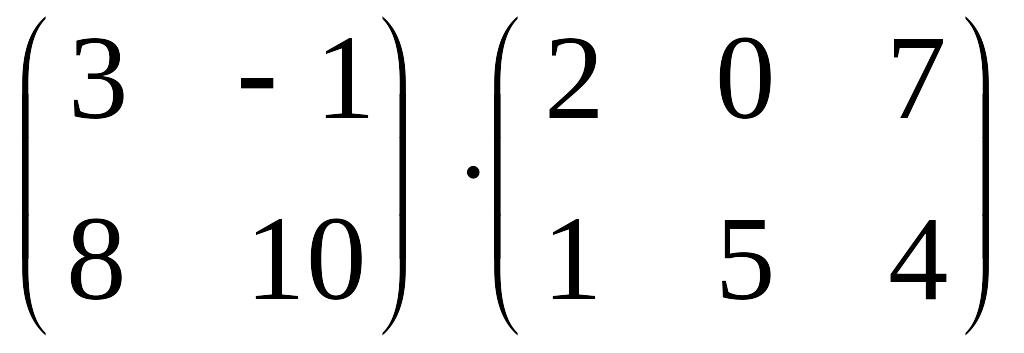 ;
б)
;
б)
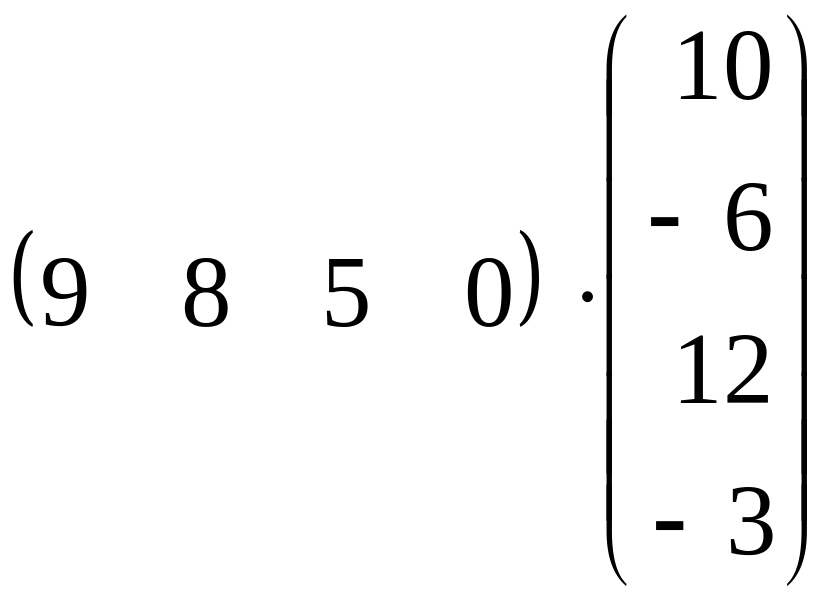 ;
в)
;
в)
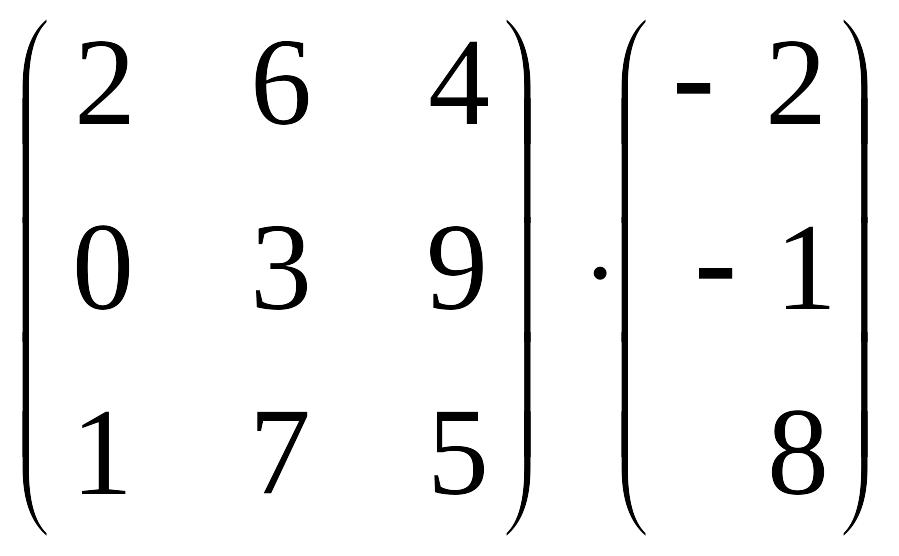 .
.
Лекція 2
