
§ 3. Обобщающие примеры по теме: «Определители 2-го и 3-го порядков»
Набор обобщающих Примеров соответствует требованиям «Семестрового плана» при изучении темы: «Определители 2-го и 3-го порядков». Эти Примеры предназначены закрепить навыки применения общих алгоритмов решений, установленных в поясняющих Примерах.
☺ ☻ ☺
Пример
1–2:
Вычислить определитель:
![]() =
=![]() .
.
Решение:
1).
Воспользуемся общей формулой вычисления:
d=![]() =
=![]() .
.
2). В нашем случае: d=1·4 – 2·3 = –2.
Ответ:d= –2.
Пример
2–5: Вычислить определитель:
![]() =
=![]() .
.
Решение:
1). Воспользуемся свойством определителя: если строки определителя пропорциональны, то определитель равен нулю.
2).
В нашем случае:
![]() .
.
Ответ:d=0.
Пример
3–8: Вычислить определитель:
![]() =
=![]() .
.
Решение:
1).
Воспользуемся общей формулой вычисления:
d=![]() =
=![]() .
.
2).
В нашем случае: d=![]() ·
·![]() –
–![]() ·
·![]() =
=![]() =–2
=–2![]() .
.
Ответ:d=0.
Пример
4–10:
Вычислить определитель:
![]() =
=![]() .
.
Решение:
1).
Воспользуемся общей формулой вычисления:
d=![]() =
=![]() .
.
2).
В нашем случае: d=![]() –
–
![]() =
=![]() .
.
Ответ:d=![]() .
.
Пример
5–14:
Вычислить
определитель 2-го порядка: d= .
.
Решение:
1). Можно было бы сразу раскрывать определитель по общей формуле, но наличие общих множителей в обеих строках (столбцах) позволяет предварительно упростить запись определителя вынесением этих множителей за знак определителя.
2).
Результат упрощений: d=![]() ·
·![]() =
=![]() ·d1:
вынесением общего множителя
·d1:
вынесением общего множителя
![]() из 1-й и 2-й строк получили для вычисления
значительно более простую форму –
определитель d1!
из 1-й и 2-й строк получили для вычисления
значительно более простую форму –
определитель d1!
3).
Вычислим:
![]() =
=![]() =
=![]() ,
тогда, очевидно, d=1.
,
тогда, очевидно, d=1.
Ответ: d =1.
Пример
6–18:
Вычислить определитель:![]() .
.
Решение:
1).
Воспользуемся общей формулой вычисления:
d=![]() =
=![]() .
.
2).
В нашем примере: d=![]() =
=![]() .
Учтено:
.
Учтено:
![]() .
.
Ответ:
![]() .
.
Пример
7–20:
Вычислить определитель:![]() =
=![]() .
.
Решение:
1).
Воспользуемся общей формулой вычисления:
d=![]() =
=![]() .
.
2).
В нашем примере: d=![]() –1·1
= 0. Учтено:
–1·1
= 0. Учтено:
![]() .
.
Ответ: d=0.
Пример
8–22:
Решить систему уравнений:
![]() по правилу Крамера.
по правилу Крамера.
Решение:
1).
Составим
определитель системы: d=![]() и определители:
и определители:
![]() =
=![]() ,
заменяя 1-й столбец определителя d
столбцом
,
заменяя 1-й столбец определителя d
столбцом
![]() правой части;
правой части;
![]() =
=![]() ,
заменяя 2-й столбец определителя d
столбцом
,
заменяя 2-й столбец определителя d
столбцом
![]() правой части.
правой части.
2).
Вычислили: d=–1,
![]() =–3,
=–3,
![]() =1
.
=1
.
3).
Применяя правило Крамера, получим:
x=![]() =3;
y=
=3;
y=![]() =–1.
=–1.
Ответ: x=3; y=–1.
Пример
9–26:
Решить систему уравнений:
![]() по правилу Крамера.
по правилу Крамера.
Решение:
1).
Составим
определитель системы: d=![]() ,
заменяя 1-й столбец определителя d
столбцом
,
заменяя 1-й столбец определителя d
столбцом
![]() правой части, получаем:
правой части, получаем:
![]() =
=![]() ,
заменяя 2-й столбец определителя d
столбцом
,
заменяя 2-й столбец определителя d
столбцом
![]() правой части, получаем:
правой части, получаем:
![]() =
=![]() .
.
2).
Вычислили: d=1,
![]() =
=
![]() ,
,
![]() =
=![]() .
.
3).
Применяя правило Крамера, получим:
x=![]() =
=![]() ;
y=
;
y=![]() =
=![]() .
.
Ответ: x=16; y=7.
Пример
10–28:
Исследовать систему уравнений:![]() используя теоретические результаты,
полученные в § 1.
используя теоретические результаты,
полученные в § 1.
Решение:
1).
Составим
определитель системы: d=![]() =0
и определители:
=0
и определители:
![]() =
=![]() =0,
заменяя 1-й столбец определителя d
столбцом
=0,
заменяя 1-й столбец определителя d
столбцом
![]() правой части;
правой части;
![]() =
=![]() =0.
заменяя 2-й столбец определителя d
столбцом
=0.
заменяя 2-й столбец определителя d
столбцом
![]() правой части. Следует: решений бесчисленное
множество → система неопределённая.
правой части. Следует: решений бесчисленное
множество → система неопределённая.
2).
Можно было сразу увидеть:
![]() → имеем одно уравнение:
→ имеем одно уравнение:
![]() с двумя неизвестными.
с двумя неизвестными.
3![]() ).
Геометрически: векторы нормалей прямых:
).
Геометрически: векторы нормалей прямых:
![]() =(4,6)
и
=(4,6)
и
![]() =(6,9)
параллельны. Легко проверить, что точка:
(–1,1) принадлежит обеим прямым → прямые
совпадают!
=(6,9)
параллельны. Легко проверить, что точка:
(–1,1) принадлежит обеим прямым → прямые
совпадают!
Ответ: при d ≠ 0 система уравнений единственное решение; при d = 0 их бесчисленное множество.
Пример
11–30:
Решить уравнение:![]() x=
x=![]() по правилу Крамера.
по правилу Крамера.
Решение:
1).
Учтём,
что линейное уравнение с одной неизвестной
– это частный случай систем уравнений.
Поэтому: d=![]() ,
,
![]() =
=
![]() .
.
2).
Тогда запишем: x=![]() =
=![]() ,
которое верно при
,
которое верно при![]() ≠0,
то есть
≠0,
то есть
![]() .
В этом случае имеем единственное решение.
.
В этом случае имеем единственное решение.
3).
Если
![]() =0,
то решений нет при
=0,
то решений нет при
![]() =
=
![]() ≠0,
так как равенство x·d
=
≠0,
так как равенство x·d
=![]() невозможно ни при каком x.
Если
невозможно ни при каком x.
Если
![]() =0
и
=0
и
![]() =0,
то решением является любое число.
=0,
то решением является любое число.
Ответ: полное исследование: в тексте.
Пример
12–40:
Доказать, что квадратный трёхчлен с
комплексными коэффициентами тогда, и
только тогда, будет полным квадратом,
если:![]() =0.
=0.
Решение:
1).
Учтём,
что линейное уравнение с одной неизвестной
– это частный случай систем уравнений.
Поэтому: d=![]() ,
,
![]() =
=
![]() .
.
2).
Тогда запишем: x=![]() =
=![]() ,
которое верно при
,
которое верно при![]() ≠0,
то есть
≠0,
то есть
![]() .
В этом случае имеем единственное решение.
.
В этом случае имеем единственное решение.
3).
Если
![]() =0,
то решений нет при
=0,
то решений нет при
![]() =
=
![]() ≠0,
так как равенство x·d
=
≠0,
так как равенство x·d
=![]() невозможно ни при каком x.
Если
невозможно ни при каком x.
Если
![]() =0
и
=0
и
![]() =0,
то решением является любое число.
=0,
то решением является любое число.
Ответ: полное исследование: в тексте.
Пример
13–43:
Вычислить определитель:![]() =
= .
.
Решение:
Вычислим определитель несколькими способами:
Способ 1. В соответствии с определением определителя 3-го порядка:
![]() =40.
=40.
Способ 2. В соответствии со свойством 9 можно вычислить определитель 3-го порядка разложением по любой строке или любому столбцу. Запишем разложение по 1-й строке:
![]() =40.
=40.
Способ 3. Используя все необходимые свойства определителя, преобразуем его до простейшего вида: в одной из строк, или в одном из столбцов заменяем все элементы, кроме одного, нулями:
d
= (1)
= =
(2)
=
=
(2)
= =
(3)
=
=
(3)
=![]() = (4)
=40.
= (4)
=40.
Операции: (1): [R2] – [R3]; [R3] – [R1]. (2): [R1] +[R2]·3. (3): применяем разложение определителя по столбцу-3. (4): завершаем вычисление.
Замечание: обозначено: C – столбец; R – строка определителя.
Ответ:d= 40.
Пример
14–46:
Вычислить определитель:![]() =
= .
.
Решение:
Применим для вычисления определителя Способ 3: этот способ допускает в широком диапазоне импровизации. При использовании этого способа не следует заранее прицеливаться к определённой строке (столбцу) для получения в ней многих нулей! Нужно за счёт операций со строками и столбцами добиться максимальной простоты чисел-элементов определителя. В некоторый момент всё становится очевидным!
d
= (1)
=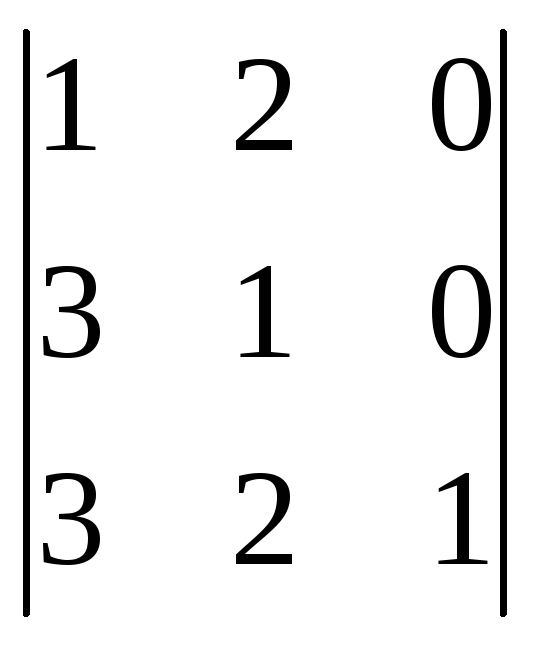 =
(2)
=
=
(2)
=![]() = (3)
=–5.
= (3)
=–5.
Операции: (1): [C3] + [C2]·2. (2): применяем разложение определителя по столбцу-3. (3): завершаем вычисление.
Ответ:d=–5.
Пример
15–56:
Вычислить определитель:![]() =
= .
.
Решение:
Применим способ-3 преобразования и вычисления определителя:
![]() =(1)=(a+b+c)·
=(1)=(a+b+c)·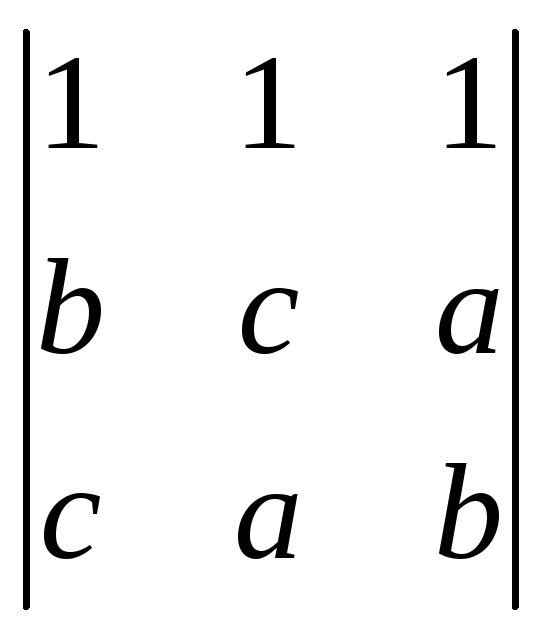 =
(2)
=(a+b+c)·
=
(2)
=(a+b+c)· =
(3)
=
=
(3)
=![]() .
.
Операции: (1): [R1]+[R2]+[R3]; выносим общий множитель за знак определителя. (2): [C3] – [C1]; [RC]–[RC]. (3): применяем разложение определителя по строке-1 и завершаем вычисление.
Ответ:d=![]() .
.
Пример
16–60:
Вычислить определитель:![]() =
= .
.
Решение:
1) Применим свойство определителя:
d
= =
d1+
d2.
=
d1+
d2.
2)
В нашем случае:
![]() =
= +
+ =
d1+d2.
Вычисление определителя d1
достаточно просто: d1
=
=
d1+d2.
Вычисление определителя d1
достаточно просто: d1
=![]() .
Вычисление определителя d2
выполним способом 3:
.
Вычисление определителя d2
выполним способом 3:
![]() =(1)=
=(1)=
 =
(2)
=
=
(2)
=
![]() →
→
![]() =
=
![]() .
.
Операции: (1): [C3] –[C1]; [C2] –[C1]. (2): учитываем, что получен определитель треугольного вида, завершаем вычисление.
Ответ:d=![]() .
.
Пример
17–65:
Показать, что определитель:![]() =
= и два других определителя, полученных
из данного круговой перестановкой
элементов
и два других определителя, полученных
из данного круговой перестановкой
элементов![]() и
и![]() ,
равны нулю, если
,
равны нулю, если![]() – длины сторон треугольника и
– длины сторон треугольника и![]() – его углы, противолежащие соответствующим
сторонам
– его углы, противолежащие соответствующим
сторонам![]() .
.
Решение:
1) Применим свойство определителя:
d
=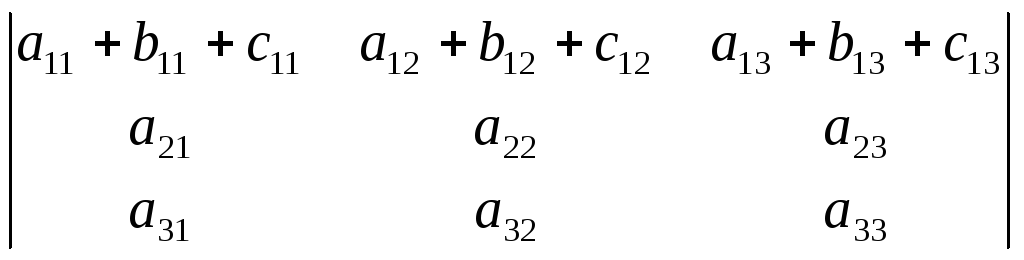 +
+ +
+ +
+
Это значит, что можно от вычисления одного громоздкого определителя перейти к вычислению трёх простых определителей: d == d1+ d2+ d3.
2)
В нашем случае: d1
= =
=![]() =
=![]() ;
;
d2
= =–
=–![]()
![]() =
=![]() ;
;
d3
=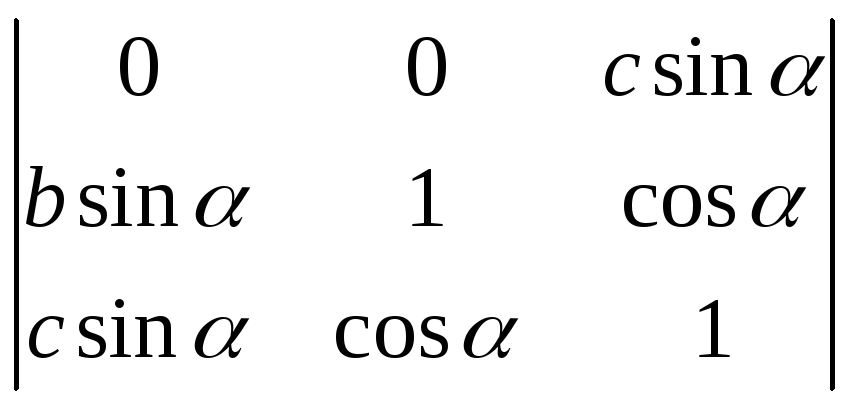 =
=![]()
![]() =
=![]() .
.
3)
Тогда получаем: d=d1+d2+d3
=
![]() .
Учитываем известную теорему косинусов
для треугольника со сторонами
.
Учитываем известную теорему косинусов
для треугольника со сторонами
![]() и углами
и углами
![]() ,
противолежащими этим сторонам. Для
стороны a:
,
противолежащими этим сторонам. Для
стороны a:
![]() ,
для стороны b:
,
для стороны b:
![]() ,
для стороны c:
,
для стороны c:
![]() .
Используя эти равенства, получаем: d=0
как для исходного определителя, так и
для получаемых из него циклической
перестановкой соответствующих сторон
и углов треугольника!
.
Используя эти равенства, получаем: d=0
как для исходного определителя, так и
для получаемых из него циклической
перестановкой соответствующих сторон
и углов треугольника!
Ответ:d=0: доказано.
Пример
18–66:
Вычислить определитель: .
.
Решение:
1) Преобразуем определитель к форме, удобной для разложения по строке или по столбцу:
d
= (1)
= =
(2)
=
=
(2)
=
 =
(3)
=–2.
=
(3)
=–2.
Операции: (1): [C3] – [C1]; вынесем общий множитель столбца-3 за знак определителя. (2): [C3] – [C1]; [C3] – [C2]. (3): завершаем вычисление для определителя треугольного вида.
Ответ:d= –2.
Пример
19–74:
Решить систему уравнений:
 пользуясь формулами Крамера.
пользуясь формулами Крамера.
Решение:
1)
Системе уравнений соответствуют: матрица
системы
A
и расширенная
матрица
![]() :
:
A
= ,
,
![]() =
= .
.
2)
Формулы Крамера в общем виде:
![]() ,
,
![]() ,
,
![]() .
Вычислим все величины, входящие в эти
формулы, для заданной системы уравнений:
.
Вычислим все величины, входящие в эти
формулы, для заданной системы уравнений:
d
= =1,
=1, ![]() =
= =3,
=3,
![]() =
= =–2,
=–2,
![]() =
= =2.
=2.
3)
Вычислим неизвестные:
![]() ,
,![]() ,
,
![]() → решение заданной системы уравнений.
→ решение заданной системы уравнений.
Ответ:
![]() ,
,![]() ,
,![]() .
.
Пример
20–82: Имеем систему уравнений:
 Установить: является эта система
совместной или несовместной. Если
система совместна, найти её решение.
Установить: является эта система
совместной или несовместной. Если
система совместна, найти её решение.
Решение:
1)
Системе уравнений соответствуют: матрица
системы
A
и расширенная
матрица
![]() :
:
A
= ,
,
![]() =
= .
.
2)
Вычислим все величины, входящие в формулы
![]() ,
,
![]() ,
,
![]() :
:
d
= =0,
=0, ![]() =
= =0,
=0,
![]() =
= =0,
=0,
![]() =
= =0.
=0.
3)
Так как
![]() и
и
![]() =0,
=0,
![]() =0,
=0,
![]() =0,
то система неопределённая: имеет
бесчисленное множество решений.
Воспользуемся геометрической иллюстрацией:
=0,
то система неопределённая: имеет
бесчисленное множество решений.
Воспользуемся геометрической иллюстрацией:
![]() =(2,–3,1),
=(2,–3,1),
![]() =(3,–5,5),
=(3,–5,5),
![]() =(5,–8,6)
–
=(5,–8,6)
– компланарны, но плоскостиα1,
α2,
α3
различны: линии их пересечения
совпадают (пучок
плоскостей!);
общие точки трех плоскостей: общая
линия пересечения. В этом случае
система имеет бесчисленное
множество решений,
говорят – система
неопределенна.
компланарны, но плоскостиα1,
α2,
α3
различны: линии их пересечения
совпадают (пучок
плоскостей!);
общие точки трех плоскостей: общая
линия пересечения. В этом случае
система имеет бесчисленное
множество решений,
говорят – система
неопределенна.
Для
исследования соответствия геометрического
образа и системы коэффициентов матрицы
![]() воспользуемся 4-мерными векторами:
воспользуемся 4-мерными векторами: ![]() ,
,
![]() ,
,
![]() .
.
В
этом случае векторы
![]() ,
,![]() ,
,![]() – линейно зависимы, причём так, что один
из них является линейной комбинацией
двух других: это следует
из уравнения пучка плоскостей!
Это значит, что фактически система
состоит из двух уравнений, и одной из
переменных можно присваивать произвольные
значения!
– линейно зависимы, причём так, что один
из них является линейной комбинацией
двух других: это следует
из уравнения пучка плоскостей!
Это значит, что фактически система
состоит из двух уравнений, и одной из
переменных можно присваивать произвольные
значения!
Ответ:система несовместна.
Пример
21–111:
Доказать тождество:d
=
 =
=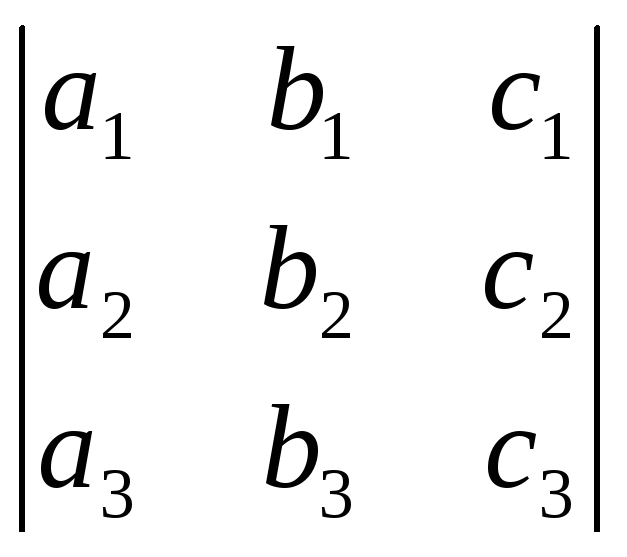 ,
не применяя вычислений правой и левой
частей тождества.
,
не применяя вычислений правой и левой
частей тождества.
Решение:
1)
Выполним Операции:
[C3]
– [C1]·x–
[C2]·y
→ получено d
= .
.
2) Тождество доказано!
Ответ:доказано: см. текст.
Пример
22–115:
Доказать тождество:d
= =
=![]() , не применяя вычислений правой и левой
частей тождества.
, не применяя вычислений правой и левой
частей тождества.
Решение:
1)
Выполним Операции:
[R3]
– [R1];
[R2]
– [R1]
→ получено d
=![]() .
Вынося общие множители строк, получаем:
d
=
.
Вынося общие множители строк, получаем:
d
=![]() ·
·![]() =
=![]() .
.
2) Тождество доказано!
Ответ:доказано: см. текст.
☻
Вопросы для самопроверки:
Может ли определитель 2-го порядка не быть числом?
Изменится ли определитель 2-го порядка, если в нем строки заменить столбцами и наоборот (проверьте!)?
Изменится ли определитель 2-го порядка, если в нем строки (или столбцы) поменять местами (проверьте!)?
Изменится ли определитель 2-го порядка, если в нем из одной строки вычесть другую строку (проверьте!)?
Изменится ли определитель 2-го порядка, если в нем из одного столбца вычесть другой столбец (проверьте!)?
Изменится ли определитель 2-го порядка, если в нем строку умножить на число 2 (проверьте!)?
Может ли определитель 3-го порядка не быть числом?
Изменится ли определитель 3-го порядка, если в нем строки заменить столбцами и наоборот (проверьте!)?
Изменится ли определитель 3-го порядка, если в нем строки (или столбцы) поменять местами (проверьте!)?
Изменится ли определитель 3-го порядка, если в нем из одной строки вычесть другую строку (проверьте!)?
Изменится ли определитель 3-го порядка, если в нем из одного столбца вычесть другой столбец (проверьте!)?
Изменится ли определитель 3-го порядка, если в нем строку умножить на число 2 (проверьте!)?
Существует ли определитель для матрицы
 ?
?
< * * * * * >
