
§ 2. Закон инерции.
Во всех рассмотренных примерах есть одно общее – непредсказуемость окончательного выражения для канонической записи квадратичной формы: всякая квадратичная форма может быть приведена к каноническому виду многими способами. В связи с этим возникают вопросы:
▫ что общего между этими различными каноническими записями одной и той же исходной квадратичной формы;
▫ можно ли невырожденным преобразованием эти различные канонические записи свести к одной и той же записи;
▫ более широко: при каких условиях можно различные канонические формы свести к одной и той же записи?
Для того, чтобы получить наиболее общие результаты, предположим, что квадратичные формы могут использовать как действительные коэффициенты, так и комплексные. В первом случае будем называть квадратичную форму комплексной, во втором – действительной.
Пусть имеем комплексную квадратичную форму. Пусть невырожденным линейным преобразованием переменных, в котором могли использоваться и комплексные числа, удалось привести квадратичную форму к каноническому виду:
f
=![]() +
+![]() +…+
+…+![]() , (4)
, (4)
где все
коэффициенты: b1,b2,…,![]() отличны
от нуля, причём
отличны
от нуля, причём
![]() - ранг
квадратичной формы.
- ранг
квадратичной формы.
Так как для комплексных чисел извлечение квадратного корня выполнимо для любых комплексных чисел, можем применить ещё одно линейное невырожденное преобразование переменных:
![]() =
=![]() ,
,![]() =
=![]() ,...,
,...,![]() =
=![]() ,
,![]() =
=![]() ,...,
,...,
![]() =
=![]() . (5)
. (5)
Выражения
(4) и (5) показывают, что любая
квадратичная форма ранга
![]() в поле комплексных чисел может быть
приведена невырожденным преобразованием
к записи:
в поле комплексных чисел может быть
приведена невырожденным преобразованием
к записи:
![]() =
=![]() +
+![]() +…+
+…+![]() , (6)
, (6)
запись квадратичной формы в виде (6) называют записью квадратичной формы в нормальном виде: все коэффициенты при квадратах переменных равны единице.
Пусть
имеем две квадратичные формы ![]() и
и ![]() одинакового ранга
одинакового ранга ![]() .
Для того, что невырожденным преобразованием
переменных перевести форму
.
Для того, что невырожденным преобразованием
переменных перевести форму ![]() в форму
в форму ![]() ,
необходимо выполнить действия:
,
необходимо выполнить действия:
A1:
перевести форму ![]() к виду:
к виду: ![]() =
=![]() +
+![]() +…+
+…+![]() .
.
A2:
перевести форму ![]() к виду:
к виду: ![]() =
=![]() +
+![]() +…+
+…+![]() .
.
A3:
от записи: ![]() =
=![]() +
+![]() +…+
+…+![]() ,
используя невырожденные преобразования
переменных формы
,
используя невырожденные преобразования
переменных формы ![]() в обратном порядке,
получаем исходную
запись квадратичной формы g.
в обратном порядке,
получаем исходную
запись квадратичной формы g.
Так как невырожденное линейное преобразование неизвестных не изменяет ранга квадратичной формы, то приходим к результату:
|
Теорема: (11.6) |
Две комплексные квадратичные формы от n неизвестных тогда и только тогда переводятся друг в друга невырожденными линейными преобразованиями с комплексными коэффициентами, если эти формы имеют один и тот же ранг. |
Следствие: каноническим видом комплексной квадратичной формы ранга r может служить всякая сумма квадратов r неизвестных с любыми отличными от нуля комплексными коэффициентами.
Пусть имеем действительную квадратичную форму. Пусть невырожденным линейным преобразованием переменных, в котором могли использоваться только действительные числа, удалось привести квадратичную форму к каноническому виду:
![]() =
=![]() +
+![]() +…+
+…+![]() –
–![]() –…–
–…–![]() . (7)
. (7)
где все
коэффициенты: b1,b2,…,![]() больше
нуля, причём
больше
нуля, причём ![]() - ранг
квадратичной формы.
- ранг
квадратичной формы.
Применим ещё одно линейное невырожденное преобразование переменных с действительными коэффициентами:
![]() =
=![]() ,
,![]() =
=![]() ,...,
,...,![]() =
=![]() ,
,![]() =
=![]() ,...,
,...,
![]() =
=![]() . (8)
. (8)
Выражения
(7) и (8) показывают, что любая
действительная квадратичная форма
ранга ![]() в поле действительных чисел может быть
приведена невырожденным преобразованием
к нормальному
виду:
в поле действительных чисел может быть
приведена невырожденным преобразованием
к нормальному
виду:
![]() =
=![]() +
+![]() +…+
+…+![]() –
–![]() –…–
–…–![]() . (9)
. (9)
Как было
отмечено, линейные преобразования
квадратичной формы допускают импровизации,
приводящие к различным каноническим
записям (7). То, что в записях вида (7) число
коэффициентов не равных нулю ![]() ,
было доказано. Остаётся выяснить, могут
ли отличаться записи (9) для одной и той
же квадратичной формы при различных
линейных преобразованиях переменных.
На этот вопрос отвечает следующая
теорема.
,
было доказано. Остаётся выяснить, могут
ли отличаться записи (9) для одной и той
же квадратичной формы при различных
линейных преобразованиях переменных.
На этот вопрос отвечает следующая
теорема.
|
Теорема: (11.7) |
Число положительных и число отрицательных квадратов в нормальном виде, к которому приводится данная квадратичная форма с действительными коэффициентами действительным невырожденным линейным преобразованием, не зависит от выбора этого преобразования. |
►Пусть
![]() =
=![]() - действительная квадратичная форма с
переменными x1,x2,…,
- действительная квадратичная форма с
переменными x1,x2,…,
![]() .
Пусть к этой квадратичной форме применены
два различных действительных невырожденных
линейных преобразований переменных:
.
Пусть к этой квадратичной форме применены
два различных действительных невырожденных
линейных преобразований переменных:
![]() =
=![]() ,
,
![]() =
1,2,…,n;
=
1,2,…,n; ![]() =
=![]() ,
,
![]() =
1,2,…,n, (10)
=
1,2,…,n, (10)
причём, преобразования (10) такие, что заданная квадратичная форма приведена ими к различным выражениям нормального вида:
f
=![]() +
+![]() +…+
+…+![]() –
–![]() –…–
–…–![]() ,
f =
,
f =![]() +
+![]() +…+
+…+
![]() –
–![]() –…–
–…–![]() .(11)
.(11)
Замечание:
учтём: все![]() =0,...,
=0,...,![]() =0
и все
=0
и все![]() =0,...,
=0,...,![]() =0
в выражениях (10); это будет играть
существенную роль в доказательстве
теоремы.
=0
в выражениях (10); это будет играть
существенную роль в доказательстве
теоремы.
Учитывая
теорему о ранге квадратичной формы,
пока что мы можем утверждать, что
слагаемых в любой записи нормального
вида одной и той же квадратичной формы
всегда ![]() .
Пусть в этих записях число положительных
слагаемых различно, причём: k
< m. Допустим, что
существуют такие значения переменных
x1,x2,…,
.
Пусть в этих записях число положительных
слагаемых различно, причём: k
< m. Допустим, что
существуют такие значения переменных
x1,x2,…,![]() ,
что будут одновременно выполнены
равенства:
,
что будут одновременно выполнены
равенства:
![]() =0,
=0,
![]() =0,...,
=0,...,![]() =0,
=0,
![]() =0,...,
=0,...,![]() =0.(12)
=0.(12)
Возможно
ли это? Для ответа на этот вопрос применим
иллюстрацию совокупности равенств
(12), приняв: ![]() =24,
=24,
![]() =15,
k =5, m
=8.
=15,
k =5, m
=8.
|
|
1 |
2 |
|
... |
5 |
6 |
... |
8 |
9 |
|
|
... |
|
|
15 |
16 |
|
... |
|
8 |
9 |
|
... |
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Всего
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из
таблицы хорошо видно, что для нахождения
множества решений системы однородных
уравнений с неизвестными: x1,x2,…,![]() ,
определяемыми условиями (10) и (11) имеется
уравнений:
,
определяемыми условиями (10) и (11) имеется
уравнений: ![]() =
=![]() <
<![]() .
Это значит, что ненулевые решения
имеются: этих решений бесчисленное
множество.
.
Это значит, что ненулевые решения
имеются: этих решений бесчисленное
множество.
Используя
одно из полученных ненулевых решений
![]() ,
,![]() ,…,
,…,![]() ,
преобразуем правые части равенств (11)
и приравняем их:
,
преобразуем правые части равенств (11)
и приравняем их:
–![]() –…–
–…–![]() =
=![]() +
+![]() +…+
+…+
![]() . (13)
. (13)
Так как
в преобразованиях неизвестных все
коэффициенты действительные числа, то
в выражении (3)
все квадраты
показанных переменных неотрицательные.
Но тогда равенство (13) возможно только
при равенстве нулю всех квадратов,
входящих в правую и левую части равенства.
Для нас важен факт, что потребовалось
равенство нулю всех переменных ![]() :
:
![]() =0,
=0,
![]() =0,...,
=0,...,![]() =0,
=0,
![]() =0,...,
=0,...,
![]() =0. (14)
=0. (14)
Но,
система равенств, с учётом выражений
(10), есть система ![]() однородных уравнений с
однородных уравнений с ![]() неизвестными: x1,x2,…,
неизвестными: x1,x2,…,![]() .
Так как линейные преобразования
переменных в квадратичных формах -
невырожденные, то определитель
системы уравнений
(14) не равен
нулю. Но, тогда
эта система уравнений имеет единственное
решение – нулевое.
Это значит, что предположение, что
возможно неравенство: k
< m не верно. Отсюда
следует, что k =m.
Так как обозначения переменных в
выражениях (10) определяется исследователем,
то и предположение: k
> m не допустимо.
◄
.
Так как линейные преобразования
переменных в квадратичных формах -
невырожденные, то определитель
системы уравнений
(14) не равен
нулю. Но, тогда
эта система уравнений имеет единственное
решение – нулевое.
Это значит, что предположение, что
возможно неравенство: k
< m не верно. Отсюда
следует, что k =m.
Так как обозначения переменных в
выражениях (10) определяется исследователем,
то и предположение: k
> m не допустимо.
◄
|
Определение: (11.3) |
В
действительной квадратичной форме:
число
k
положительных
квадратов называют
положительным
индексом инерции,
а
число
|
Следствие:
Если имеем две квадратичные формы от ![]() неизвестных и их ранги совпадают, то,
очевидно, они приводятся к одной и той
же нормальной форме: у них совпадают и
ранги, и положительные индексы, а значит,
и отрицательные индексы, и сигнатуры!
Это можно считать условием перевода
одной квадратичной формы в другую.
неизвестных и их ранги совпадают, то,
очевидно, они приводятся к одной и той
же нормальной форме: у них совпадают и
ранги, и положительные индексы, а значит,
и отрицательные индексы, и сигнатуры!
Это можно считать условием перевода
одной квадратичной формы в другую.
Для того, чтобы квадратичная форма приводилась к нормальному виду, где имеются только положительные слагаемые, нужно, чтобы положительный индекс инерции формы совпадал с ее рангом.
Продолжим рассмотрение примеров, иллюстрирующих процесс преобразований переменных квадратичной формы.
☺☺
Пример
11–05:Методом Лагранжа
найти нормальный вид и невырожденное
линейное преобразование, приводящее к
этому виду квадратичную форму: f
=![]() .
.
.
Решение:
1). Так как в записи формы есть невыделенные квадратыпеременных, то применим преобразованиеR1. Изобразим наши действия при помощи таблицы, выделяя основные штрихи наблюдений:
|
|
|
|
|
|
|
|
|
|
|
|
Замена: |
|
|
| ||||||||||
|
|
1 |
1 |
-2 |
|
= |
|
1 |
1 |
-2 |
|
|
|
1 |
1 |
-2 |
| ||||||||
|
|
1 |
|
|
|
|
1 |
5 |
0 |
|
|
0 |
1 |
0 |
| ||||||||||
|
|
-2 |
|
|
|
|
-2 |
0 |
-4 |
|
|
0 |
0 |
1 |
| ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*Левый рисунок матрицы
![]() показывает, что имеетсяневыделенный
квадрат
переменной
показывает, что имеетсяневыделенный
квадрат
переменной ![]() при наличии в записи слагаемого
при наличии в записи слагаемого ![]() и слагаемых:
и слагаемых: ![]() ,
куда переменная
,
куда переменная
![]() входит сомножителем.
Всё это сигналит:нужно
применять преобразование R1.
Средний рисунок матрицы
входит сомножителем.
Всё это сигналит:нужно
применять преобразование R1.
Средний рисунок матрицы
![]() показывает, что мы наметили в записи
формы
показывает, что мы наметили в записи
формы![]() выделить квадрат переменной
выделить квадрат переменной
![]() ,
причём так, чтобы переменная
,
причём так, чтобы переменная
![]() не использовалась, как сомножитель в
других слагаемых этой формы. Таблица
замены показывает необходимое
преобразование переменных: видим, как
используются коэффициенты первой строки
матрицы среднего рисунка. Матрица
не использовалась, как сомножитель в
других слагаемых этой формы. Таблица
замены показывает необходимое
преобразование переменных: видим, как
используются коэффициенты первой строки
матрицы среднего рисунка. Матрица
![]() отражает преобразование переменных:
отражает преобразование переменных:
![]() =
= ·
·![]() ,
или
,
или![]() =
=![]() ·
·![]() . (1.1)
. (1.1)
Для
замены в заданной форме переменной ![]() на переменную
на переменную ![]() из преобразования (1.1)
легко получить обратное преобразование:
из преобразования (1.1)
легко получить обратное преобразование:
![]() =
= ·
·![]() ,
или
,
или ![]() =
=![]() ·
·![]() .
(1.2)
.
(1.2)
Подставляя
выражения ![]() ,
,![]() ,
,![]() в исходную запись формы
в исходную запись формы
![]() ,
в результате
невырожденного линейного преобразования
переменных
,
в результате
невырожденного линейного преобразования
переменных
![]() получим новое выражение формы
получим новое выражение формы
![]() ,
в которой выделен
квадрат неизвестной
,
в которой выделен
квадрат неизвестной
![]() :
:
![]() =
=![]() .
(1.3)
.
(1.3)
2). Так как в записи
формы есть невыделенные
квадратынеизвестных, то применим
преобразованиеR1,
причём станем выделять квадрат переменной![]() :
:
![]() =
= ·
·![]() ,
или
,
или ![]() =
=![]() ·
·![]() .
(1.4)
.
(1.4)
Для
замены в форме (1.3)
переменной ![]() на переменную
на переменную ![]() из преобразования (1.4)
легко получить обратное преобразование:
из преобразования (1.4)
легко получить обратное преобразование:
![]() =
= ·
·![]() ,
или
,
или ![]() =
=![]() ·
·![]() .
(1.5)
.
(1.5)
Подставляя
выражения ![]() ,
,![]() ,
,![]() в запись (1.3)
формы
в запись (1.3)
формы
![]() ,
в результате
невырожденного линейного преобразования
переменных
,
в результате
невырожденного линейного преобразования
переменных
![]() получим новое выражение формы
получим новое выражение формы
![]() ,
в которой выделены
квадраты всех
неизвестных. Получена запись квадратичной
формы в каноническом виде:
,
в которой выделены
квадраты всех
неизвестных. Получена запись квадратичной
формы в каноническом виде:
![]() =
=![]() .
(1.6)
.
(1.6)
3). Применим
преобразование:
![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =3
=3![]() ,
то есть:
,
то есть:![]() =
=![]() ·
·![]() .
Тогда квадратичная форма приобретает
нормальный вид:
.
Тогда квадратичная форма приобретает
нормальный вид:![]() =
=![]() .
(1.7)
.
(1.7)
4). Воспользуемся
цепочкой преобразований переменных
![]() :
:
![]() =
=![]() –
–![]()
![]() +
+![]()
![]() ,
,
![]() =
=![]()
![]() –
–![]()
![]() ,
,
![]() =
=![]() . (1.8)
. (1.8)
Ответ:
нормальный вид формы:
![]() =
=![]() .
Невырожденное линейное преобразование,
переводящее форму
.
Невырожденное линейное преобразование,
переводящее форму
![]() к каноническому виду:
к каноническому виду:![]() =
= ·
·![]() .
.
Пример
11–06:
Заданы две квадратичные формы:
![]() =
=![]() и
и
![]() =
=![]() .
Найти невырожденное линейное преобразование
переменных, переводящее форму
.
Найти невырожденное линейное преобразование
переменных, переводящее форму
![]() в форму
в форму![]() .
.
Решение:
Общая схема решения задачи:
A1:
приводим форму
![]() к нормальному виду и определяем выражения
новых переменных через старые.
к нормальному виду и определяем выражения
новых переменных через старые.
A2:
приводим форму
![]() к нормальному виду и определяем выражения
старых переменных через новые.
к нормальному виду и определяем выражения
старых переменных через новые.
A3:
определяем линейное преобразование:![]() =
=![]() ,
,![]() =
=![]() .
.
A1:приводим форму
![]() к нормальному виду.
к нормальному виду.
1). Так как в записи формы есть невыделенные квадратыпеременных, то применим преобразованиеR1. Изобразим наши действия при помощи таблицы, выделяя основные штрихи наблюдений:
|
|
|
|
|
|
|
|
|
|
|
|
Замена: |
|
|
| ||||||||||
|
|
2 |
4 |
-2 |
|
= |
|
2 |
4 |
-2 |
|
|
|
2 |
4 |
-2 |
| ||||||||
|
|
4 |
|
|
|
|
4 |
9 |
-5 |
|
|
0 |
1 |
0 |
| ||||||||||
|
|
-2 |
|
|
|
|
-2 |
-5 |
3 |
|
|
0 |
0 |
1 |
| ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*Левый рисунок матрицы
![]() показывает, что имеетсяневыделенный
квадрат
переменной
показывает, что имеетсяневыделенный
квадрат
переменной ![]() при наличии в записи слагаемого
при наличии в записи слагаемого ![]() и слагаемых:
и слагаемых: ![]() ,
куда переменная
,
куда переменная
![]() входит сомножителем.
Всё это сигналит:нужно
применять преобразование R1.
Средний рисунок матрицы
входит сомножителем.
Всё это сигналит:нужно
применять преобразование R1.
Средний рисунок матрицы
![]() показывает, что мы наметили в записи
формы
показывает, что мы наметили в записи
формы![]() выделить квадрат переменной
выделить квадрат переменной
![]() ,
причём так, чтобы переменная
,
причём так, чтобы переменная
![]() не использовалась, как сомножитель в
других слагаемых этой формы. Таблица
замены показывает необходимое
преобразование переменных: видим, как
используются коэффициенты первой строки
матрицы среднего рисунка. Матрица
не использовалась, как сомножитель в
других слагаемых этой формы. Таблица
замены показывает необходимое
преобразование переменных: видим, как
используются коэффициенты первой строки
матрицы среднего рисунка. Матрица
![]() отражает преобразование переменных:
отражает преобразование переменных:
![]() =
= ·
·![]() ,
или
,
или![]() =
=![]() ·
·![]() . (1.1)
. (1.1)
Для
замены в заданной форме переменной ![]() на переменную
на переменную ![]() из преобразования (1.1)
легко получить обратное преобразование:
из преобразования (1.1)
легко получить обратное преобразование:
![]() =
=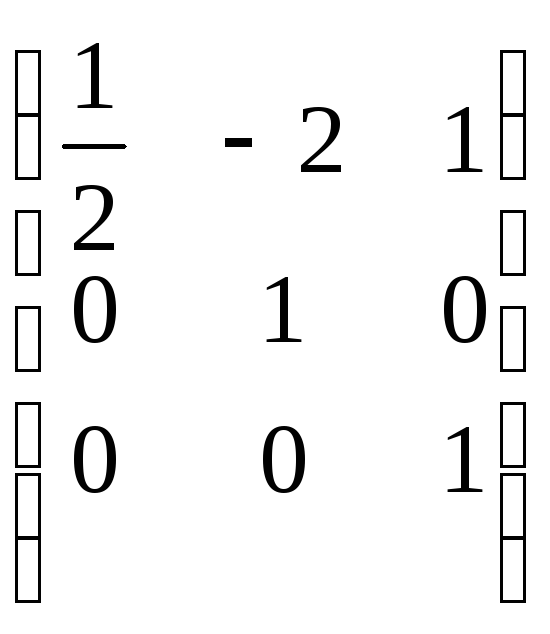 ·
·![]() ,
или
,
или ![]() =
=![]() ·
·![]() .
(1.2)
.
(1.2)
Подставляя
выражения ![]() ,
,![]() ,
,![]() в исходную запись формы
в исходную запись формы
![]() ,
в результате
невырожденного линейного преобразования
переменных
,
в результате
невырожденного линейного преобразования
переменных
![]() получим новое выражение формы
получим новое выражение формы
![]() ,
в которой выделен
квадрат неизвестной
,
в которой выделен
квадрат неизвестной
![]() :
:
![]() =
=![]() .
(1.3)
.
(1.3)
2). Так как в записи
формы есть невыделенные
квадратынеизвестных, то применим
преобразованиеR1,
причём станем выделять квадрат переменной![]() :
:
![]() =
= ·
·![]() ,
или
,
или ![]() =
=![]() ·
·![]() .
(1.4)
.
(1.4)
Для
замены в форме (1.3)
переменной ![]() на переменную
на переменную ![]() из преобразования (1.4)
легко получить обратное преобразование:
из преобразования (1.4)
легко получить обратное преобразование:
![]() =
= ·
·![]() ,
или
,
или ![]() =
=![]() ·
·![]() .
(1.5)
.
(1.5)
Подставляя
выражения ![]() ,
,![]() ,
,![]() в запись (1.3)
формы
в запись (1.3)
формы
![]() ,
в результате
невырожденного линейного преобразования
переменных
,
в результате
невырожденного линейного преобразования
переменных
![]() получим новое выражение формы
получим новое выражение формы
![]() ,
в которой выделены
квадраты всех
неизвестных. Получена запись квадратичной
формы в каноническом виде:
,
в которой выделены
квадраты всех
неизвестных. Получена запись квадратичной
формы в каноническом виде: ![]() =
=![]() .
(1.6)
.
(1.6)
3). Если применим
преобразование:
![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,
то запись квадратичной формы приобретает
нормальный вид:
,
то запись квадратичной формы приобретает
нормальный вид:![]() =
=![]() .
(1.7)
.
(1.7)
4). Воспользуемся цепочкой преобразований переменных:
![]() =
=![]() =
=![]()
![]() =
=![]() (2
(2![]() +4
+4![]() –2
–2![]() )=
)=![]() (
(![]() +2
+2![]() –
–![]() ),
),
![]() =
=![]() =
=![]() –
–![]() =
=![]() –
–![]() ,
,![]() =
=![]() =
=![]() =
=![]() ,
,
A2:приводим форму
![]() к нормальному виду.
к нормальному виду.
1). Так как в записи
формы:
![]() =
=![]() естьневыделенные
квадратыпеременных, то применим
преобразованиеR1.
Изобразим наши действия при помощи
таблицы, выделяя основные штрихи
наблюдений:
естьневыделенные
квадратыпеременных, то применим
преобразованиеR1.
Изобразим наши действия при помощи
таблицы, выделяя основные штрихи
наблюдений:
|
|
|
|
|
|
|
|
|
|
|
|
Замена: |
|
|
| ||||||||||
|
|
2 |
-2 |
-2 |
|
= |
|
2 |
-2 |
-2 |
|
|
|
2 |
-2 |
-2 |
| ||||||||
|
|
-2 |
|
|
|
|
-2 |
3 |
4 |
|
|
0 |
1 |
0 |
| ||||||||||
|
|
-2 |
|
|
|
|
-2 |
4 |
6 |
|
|
0 |
0 |
1 |
| ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*Левый рисунок матрицы
![]() показывает, что имеетсяневыделенный
квадрат
переменной
показывает, что имеетсяневыделенный
квадрат
переменной ![]() при наличии в записи слагаемого
при наличии в записи слагаемого ![]() и слагаемых:
и слагаемых: ![]() ,
куда переменная
,
куда переменная
![]() входит сомножителем.
Всё это сигналит:нужно
применять преобразование R1.
Средний рисунок матрицы
входит сомножителем.
Всё это сигналит:нужно
применять преобразование R1.
Средний рисунок матрицы
![]() показывает, что мы наметили в записи
формы
показывает, что мы наметили в записи
формы![]() выделить квадрат переменной
выделить квадрат переменной
![]() ,
причём так, чтобы переменная
,
причём так, чтобы переменная
![]() не использовалась, как сомножитель в
других слагаемых этой формы. Таблица
замены показывает необходимое
преобразование переменных: видим, как
используются коэффициенты первой строки
матрицы среднего рисунка. Матрица
не использовалась, как сомножитель в
других слагаемых этой формы. Таблица
замены показывает необходимое
преобразование переменных: видим, как
используются коэффициенты первой строки
матрицы среднего рисунка. Матрица
![]() отражает преобразование переменных:
отражает преобразование переменных: ![]() =
= ·
·![]() ,
или
,
или![]() =
=![]() ·
·![]() . (2.1)
. (2.1)
Для
замены в заданной форме переменной ![]() на переменную
на переменную ![]() из преобразования (1.1)
легко получить обратное преобразование:
из преобразования (1.1)
легко получить обратное преобразование:
![]() =
= ·
·![]() ,
или
,
или ![]() =
=![]() ·
·![]() .
(2.2)
.
(2.2)
Подставляя
выражения ![]() ,
,![]() ,
,![]() в исходную запись формы
в исходную запись формы
![]() ,
в результате
невырожденного линейного преобразования
переменных
,
в результате
невырожденного линейного преобразования
переменных
![]() получим новое выражение формы
получим новое выражение формы
![]() ,
в которой выделен
квадрат неизвестной
,
в которой выделен
квадрат неизвестной
![]() :
:
![]() =
=![]() .
(2.3)
.
(2.3)
2). Так как в записи
формы есть невыделенные
квадратынеизвестных, то применим
преобразованиеR1,
причём станем выделять квадрат переменной![]() :
:
![]() =
= ·
·![]() ,
или
,
или ![]() =
=![]() ·
·![]() .
(2.4)
.
(2.4)
Для
замены в форме (1.3)
переменной ![]() на переменную
на переменную ![]() из преобразования (1.4)
легко получить обратное преобразование:
из преобразования (1.4)
легко получить обратное преобразование:
![]() =
= ·
·![]() ,
или
,
или ![]() =
=![]() ·
·![]() .
(2.5)
.
(2.5)
Подставляя
выражения ![]() ,
,![]() ,
,![]() в запись (2.3)
формы
в запись (2.3)
формы
![]() ,
в результате
невырожденного линейного преобразования
переменных
,
в результате
невырожденного линейного преобразования
переменных
![]() получим новое выражение формы
получим новое выражение формы
![]() ,
в которой выделены
квадраты всех
неизвестных. Получена запись квадратичной
формы в каноническом виде:
,
в которой выделены
квадраты всех
неизвестных. Получена запись квадратичной
формы в каноническом виде: ![]() =
=![]() .
(2.6)
.
(2.6)
3). Если применим
преобразование:
![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,
то квадратичная форма примет вид:
,
то квадратичная форма примет вид:
![]() =
=![]() .
(2.7)
.
(2.7)
4). Воспользуемся цепочкой преобразований переменных:
![]() =
=![]() =
=![]()
![]() =
=![]() (2
(2![]() –2
–2![]() –2
–2![]() )=
)=![]() (
(![]() –
–![]() –
–![]() ),
),
![]() =
=![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() =
=![]() ,
,
A3:определяем
линейное преобразование:![]() =
=![]() ,
,![]() =
=![]() .
.
1). Приравниваем
переменные
![]() ,
полученные преобразованием квадратичных
форм
,
полученные преобразованием квадратичных
форм
![]() и
и
![]() :
:
![]() =
=![]() →
→![]() (
(![]() +2
+2![]() –
–![]() )=
)=![]() (
(![]() –
–![]() –
–![]() )→
)→![]() +2
+2![]() –
–![]() =
=![]() –
–![]() –
–![]() ,
,
![]() =
=![]() →
→![]() –
–![]() =
=![]() ,
,![]() =
=![]() →
→![]() =
=![]() . (3.1)
. (3.1)
2). Разрешаем
равенства (3.1) относительно переменных
![]() ,
,![]() ,
,![]() :
:
![]() =
=![]() –3
–3![]() –6
–6![]() ,
,![]() =
=![]() +3
+3![]() ,
,![]() =
=![]() .
.
Замечание:
к выполнению операции A3
мы приступили, убедившись, что формы
![]() и
и
![]() имеют одинаковые ранги и положительные
индексы инерции при отсутствии
отрицательных слагаемых в нормальной
записи обеих форм.
имеют одинаковые ранги и положительные
индексы инерции при отсутствии
отрицательных слагаемых в нормальной
записи обеих форм.
Ответ:
нормальный вид формы:
![]() =
=![]() =
=![]() .
Невырожденное линейное преобразование
переменных, переводящее форму
.
Невырожденное линейное преобразование
переменных, переводящее форму
![]() в форму
в форму![]() :
:![]() =
=![]() –3
–3![]() –6
–6![]() ,
,![]() =
=![]() +3
+3![]() ,
,![]() =
=![]() .
.
☻
