272

ЛА: Глава 11

Глава 11. Квадратичные формы.

При изучении теории систем линейных уравнений мы видели, что каждое уравнение системы представляло собой выражение, в которое входили переменные величины: x₁,x₂,…, в первой степени:

=,

причём начало таким конструкциям положили простейшие: с участием только двух переменных величин x₁,x₂. По мере развития теории было получено обобщение таких выражений для произвольного числа участников x₁,x₂,…,. Выражения имеют специальное название – линейные формы.

Какова история появления квадратичных форм? Ответ даёт практика деятельности человека! Начало было положено в теории кривых 2-го порядка, располагаемых произвольно на плоскости прямоугольной системы координат . Общим выражением для всех таких кривых явилось выражение:

, (1)

где коэффициенты при переменных величинах x, y: , - действительные числа. Для развития теории кривых 2-го порядка объектом исследования определили левую часть выражения (1):

=. (2)

Заметили, что все кривые 2-го порядка имеют центр: такую точку, что параллельным переносом начала координат в эту точку можно получить для той же кривой аналитическое выражение в виде:

=, (3)

именно его и назвали квадратичной формой для переменных x, y: каждое слагаемое имеет или квадрат переменной величины, или произведение двух переменных величин.

Изучение выражений (3) обнаружило их свойство: за счёт поворота системы координат на некоторый угол удаётся избавиться от слагаемого, содержащего произведение переменных, и получить, так называемый, канонический вид выражения для квадратичной формы:

=. (4)

Заметим отдельно, что поворот системы координат на угол можно толковать как линейное преобразование переменных:

или , или ,

где - невырожденная матрица преобразования: её определитель равен 1.

Изучение поверхностей 2-го порядка привело к ближайшему обобщению рассматриваемых выражений:

= → =. (5)

Замечание: для простоты восприятия алгебраического образа обозначение коэффициентов в выражениях (2)(5) не изменяется.

В пространстве для получения канонического вида квадратичной формы применяют три поворота системы координат на углы Эйлера.

Пусть имеем две системы координат , считаем эту систему координат исходной, и - система координат, подвижная от­носительно исходной – вращается относительно точки O.

Положение системы относительно можно было бы определить девятью направляющими косинусами подвижных осей, то есть косинусами тех углов, которые каждая из подвижных осей образует с неподвижными осями: это определило бы квадратную матрицу линейного преобразования переменных x, y, z.

Значительно проще и удобнее определять положение системы относительно при помощи углов Эйлера ,, , которые называют (взято из астроно­мии!): – угол прецессии, – угол нутации, – угол собственного вращения.

Это делают так. Обозначим линию пересечения плоскостей OXY и через ON – ли­ния узлов. Систему осей переводят в положение при помощи трех вращений:

первый поворот: систему осей поворачиваем вокруг оси OZ на угол так, чтобы ось OX совпала с линией уз­лов ON: система переходит в систему :

или , или ,

где - невырожденная матрица преобразования: её определитель равен 1;

второй поворот: систему осей поворачиваем вокруг оси ON на угол так, чтобы ось OZ совпала с осью : система переходит в систему :

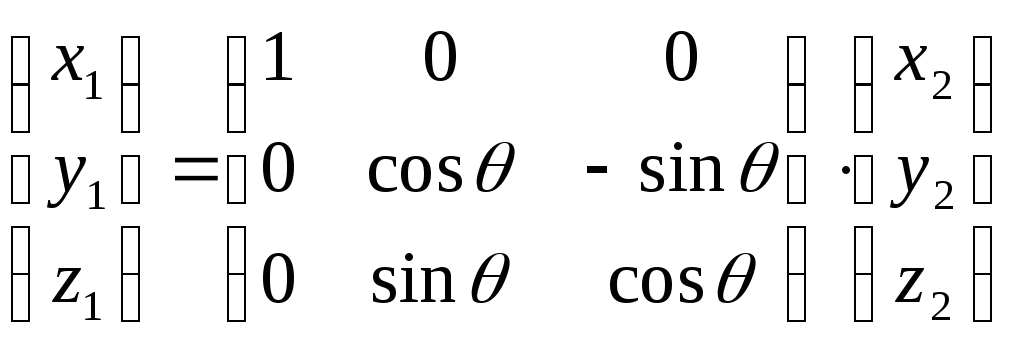или , или ,

где - невырожденная матрица преобразования: её определитель равен 1;

третий поворот: систему осей поворачиваем вокруг оси на угол так, чтобы ось ON совпала с осью : система переходит в систему :

или , или ,

где - невырожденная матрица преобразования: её определитель равен 1.

Учитывая свойства линейных преобразований, определить полное линейное преобразование, как преобразование, заданное матрицей: , причём, невырожденное.