
dsd11-12 / dsd-11=ТКС / full
.pdf
ω1 = 2Tπ - основнаячастота.
Отыскание ряда Фурье для сложного гармонического сигнала, называется гармоническим или спектральным анализом. Составляющие этого ряда - циклические частоты, которые равны ω,2ω,3ω и т.д., называются соответственно первой (основной), второй, третьей и т.д. гармониками сложногосигнала.
Каждая гармоника ряда Фурье характеризуется амплитудой Am и начальной фазой ϕm, и для коэффициентов разложения (2.3а) можно запи-
сать: am=Amcosϕm, bm=Amsinϕm.
Откуда |
A |
= |
|
a |
2 + b2 , и |
bm |
= tgϕ |
m |
. |
||||||
|
|
||||||||||||||
|
|
|
|
m |
|
|
m |
m |
am |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда единственное решение (2.3) |
представляется в более удобном |
||||||||||||||
виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S(t) = |
a |
0 |
+ |
∞ |
|
A |
|
cos(m ω t −ϕ |
|
) |
|
( 2.4 ) |
|||
|
∑ |
|
|
m |
|
||||||||||
2 |
|
|
|
||||||||||||
|
|
m = |
1 |
m |
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример1.1 Найти спектральное преобразование последовательности прямо-
угольных импульсов спараметрами(см. рис.2.1а) четнымиотносительно t = 0 , T - период сигнала, τ - длительность импульса, A - амплитуда им-
пульса. |
|
|
|
|
|
|
|
|
|
|
|
|
Отношение |
T |
|
= q |
называетсяскважностьимпульсов. |
||||||||
τ |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||
Используя(2.3а), имеем: |
|
|
|
|
|
|
||||||
|
|
|
|
2 T |
2 τ / 2 |
2 |
|
2A |
; |
|||
|
a |
= |
|
∫S(t)dt = |
|
∫ Adt = |
|
τ A = |
|
|||
|
|
|
|
|
||||||||
|
0 |
T −T |
T −τ./ 2 |
T |
|
q |
|
|||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
18 |
|
|
|
|
||

a |
|
= |
|
2 T |
S(t)cos(mω t)dt = |
|
2 τ / 2 |
Acos(mω t)dt |
= |
2A |
sin mω t |
1 |
|
|
|
|
τ / 2 |
= |
|
ω |
= |
2π |
|
= |
A |
m2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
∫ |
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|||||||||||||||||||
|
|
T |
|
T |
|
|
T |
mω |
|
|
Т |
mπ |
T |
|||||||||||||||||||||||||||||
m |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|||||||||||||||||
|
|
|
|
|
−T |
|
|
|
|
|
|
|
|
|
−τ / 2 |
|
|
|
|
|
|
|
|
|
1 |
|
−τ / 2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
A |
|
|
mπτ |
|
mπτ |
|
|
|
2A |
|
|
mπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
|
|
|
sin |
|
|
−sin − |
|
|
|
|
|
= |
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
T |
|
|
mπ |
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
mπ |
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
b |
|
= |
2 |
T |
S(t)sin(mω t)dt |
2 |
|
τ / 2 |
Asin(mω t)dt = − |
2A |
cos mω t |
|
1 |
|
τ / 2 |
= 0 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
∫ |
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
T |
T |
|
|
|
T |
|
mω |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
m |
|
−T |
|
|
1 |
|
−τ / 2 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
−τ / 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Используя выражение (2.3) для представления спектрального разложениясигнала, получим:
S(t)
=qA
=qА
|
2 A |
|
|
∞ |
2 A |
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
mπ |
|
|
|
+ 0] |
|
|
|
|
|
|
|
|
|
|||||||||||||
= |
|
|
+ |
|
∑ |
|
|
|
|
|
cos m |
|
|
t |
= |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
q |
2 |
|
m =1 mπ |
|
q |
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mπ |
|
|
|
||||
|
|
|
∞ |
|
|
|
mπ |
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2π |
|
A |
|
|
q |
|
|||||||||||||||||
|
|
|
sin q |
|
|
|
|
|
sin |
|
|
|
|||||||||||||||||||
1 |
+ 2 |
|
∑ |
|
|
|
|
cos m |
|
|
t |
= |
|
|
1 |
+ 2 ∑ |
|
|
|
|
|
|
|
cos(m ωt) |
= |
||||||
|
|
|
mπ |
|
T |
q |
|
|
mπ |
|
|||||||||||||||||||||
|
|
m =1 |
|
|
|
|
|
|
|
m =1 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
+ 2∑An cos(m ωt) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
m=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
mπ |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
sin |
q |
|
|
где |
An = |
|
|
. График такого спектрального разложения, для двух |
|
mπ |
|
||||
|
|
|
|
||
q
крайнихслучаев, когда q >> 1(T >>τ) и q ≈1(T ≈τ) , показаннарис.2.1б.
Спектральное разложение периодического сигнала можно получить, используя в качестве базиса ортонормированных функций экспоненты с мнимымпоказателем, т.е.
U |
0 |
= 1 ; |
U |
= exp(jω1t); |
||
|
|
T |
|
1 |
T |
|
|
|
|
|
|
||
U |
2 |
= exp(2 jω1t); |
U |
3 |
= exp(3 jω1t); |
|
|
T |
|
T |
|||
|
|
|
|
|
||
|
|
|
19 |
|
|
|

T |
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-τ/2 |
τ/2 |
|
τ |
t |
|
S(t) |
S(t) |
|
|
A/q |
A/q |
|
|
|
а)
2π / T |
2π /τ |
ω |
q ≈1, |
T ≈τ |
ω |
q >> 1, |
T >> τ |
|
|
|
|
короткиеимпульсы, идущиеоченьредко |
|
|
длинныеимпульсы, идущиечасто |
||
б)
Рис.2.1 Спектральноепреобразованиепоследовательностипрямоугольныхимпульсов: а- видипараметрыпрямоугольныхимпульсов, б- спектральноепреобразование
20

|
|
|
|
|
|
|
U |
k |
= exp(kjω1t) |
, |
|
|
|
|
|
гдеk = 0, ±1, ±2... |
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ТогдарядФурьепринимаетвид: |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
S(t) = 1 |
∞ |
|
C |
|
e jnω1t |
, |
(2.5) |
|||
|
|
|
|
|
|
|
∑ |
|
n |
||||||||
|
|
|
|
|
|
|
|
|
T n = −∞ |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Cn |
= 1 |
T / 2 |
|
|
|
|
|
|
|
|
|
|
||||
где |
∫ |
S(t) e− jnω1tdt , Cn - коэффициентырядаФурье. |
|||||||||||||||
|
|
|
|
T −T / 2 |
|
|
|
|
|
|
|
|
|
|
|||
|
Разложение(2.5) иногдапредставляютвболееудобномвиде |
||||||||||||||||
|
|
|
|
|
|
|
|
|
S(t) = |
∞ |
C |
|
e jnω1t , |
|
(2.5а) |
||
|
|
|
|
|
|
|
|
|
∑ |
n |
|
||||||
|
|
|
|
|
|
|
|
|
n = −∞ |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
C |
|
= |
1 |
|
T / 2 |
S(t) e− jnω1tdt |
|
|
|
|
|
|
|
|
||
n |
|
∫ |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
T −T / 2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Выражения (2.5) и (2.5а) являются разложением ряда Фурье в комплекснойформе.
Так как n принимает значения от -∞ до +∞, то из (2.5а) видно, что спектр сигнала содержит компоненты как с положительными, так и с отрицательными частотами. Обычно их объединяют в пары, т.е. по формулеЭйлера
|
|
|
|
|
|
|
|
j ω t + ϕ |
|
|
|
|
− j ω t + ϕ |
|
|
− jωt |
jωt |
|
|||||||
|
|
e jω1t + C |
|
e− jϖ1t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ e |
|
|
||||
C |
|
|
|
|
e |
1 |
|
|
n + |
|
C |
|
e |
1 |
n = |
cosωt = |
e |
|
|
||||||
n |
n |
= |
C |
n |
|
n |
|
= |
|||||||||||||||||
|
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
Cn |
|
cos(nω1t + ϕn ) |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
напряжения |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Отрицательной |
|
частоте |
|
|
соответствует |
вектор |
|||||||||||||||||
(см.рис.2.2) из разложения (2.5), вращающийся по часовой стрелки, а положительнойчастотевекторвращающийсяпротивчасовойстрелки.
21

Im
Cn=|Cn|
+ω |
Re |
-ω
C-n=|Cn|
Рис.2.2 КомплексноепредставлениегармоникрядаФурье
2.2. Спектральнаяплотностьсигнала
Пусть S(t) - одиночный импульсный сигнал. Чтобы найти его спек-
тральное разложение надо мысленно дополнить его такими же сигналами периодически следующими через T. Тогда используя спектральное разложениевкомплекснойформеможнозаписать:
|
|
S (t) = |
∞ |
C |
|
e jnω1t |
|
|
||||
|
|
∑ |
|
|
|
|||||||
|
|
|
• |
n = −∞ |
|
n |
|
|
|
|
|
|
скоэффициентамиразложения: |
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
T / 2 |
|
|
|
|
− |
jn |
ω |
1t dt |
C |
n |
= |
∫ S (t) e |
|
|
|||||||
T |
|
|
|
|||||||||
|
|
− T / 2 |
|
|
|
|
|
|
|
|||
Чтобы вернуться к одиночному импульсу надо период Т устремить |
||||||||||||
в бесконечность Т → ∞ , тогда частоты nω1 |
и (n +1)ω1 будут сколь угод- |
|||||||||||
ноблизкидругкдругуиихможнозаменитьнатекущуючастоту ω
22
|
|
|
|
|
|
|
|
1 |
∞ |
|
|
|
e− jωt dt |
|
( 2.6) |
|||
|
|
|
|
C |
n |
= |
∫ S(t) |
|
||||||||||
|
|
|
|
T |
|
|||||||||||||
|
|
|
|
|
|
|
− ∞ |
|
|
|
|
|
|
|
|
|||
Тогда коэффициенты ряда Фурье образуют комплексно- |
||||||||||||||||||
сопряженные пары C |
n |
= A e jϕn |
и C |
− n |
= A e− jϕn , и каждой паре соответ- |
|||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
||
ствуетгармоническоеколебаниевида: |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
j nω t + ϕ |
n |
|
A e |
− j nω t + ϕ |
|
|
|||||||
|
|
|
|
A e |
|
1 |
|
+ |
|
1 |
n = |
|
||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
или осуществляя предельный переход, т.е. когда nω1 мало отличает- |
||||||||||||||||||
сяот (n +1)ω1 , получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
+ ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
j ωt + ϕ |
|
− j ωt |
|
|
|
|
|
cos(ωt |
+ ϕ |
|
) |
|
|
|||||
A e |
n |
+ A e |
|
|
|
|
n = 2A |
|
n |
|
|
|||||||
n |
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
Рассмотрим бесконечно малый интервал Δω. В рамках этого интер- |
||||||||||||||||||
вала будет содержаться N пар спектральных составляющих N = ω |
= ωT |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
(так как ω1=2π/T) с коэффициентами разложения Сn (2.6 ), представляющими собой комплексную амплитуду соответствующего единичного гармоническогоколебания, т.е.
|
|
1 |
∞ |
|
|
A |
= |
∫ S(t) e jωtdt |
(2.7) |
||
T |
|||||
ω |
|
− ∞ |
|
||
|
|
|
|
Так как в рамках интервала Δω таких колебаний будет N, то полную комплексную эквивалентную амплитуду получим, домножив (2.7) на 2 и N, т.к. спектрсигналасодержиткомплексносопряженныепары.
|
|
2N |
∞ |
2 |
ω T |
∞ |
|
A |
= |
∫ S(t) e jωtdt = |
∫ S(t) e jωtdt |
||||
|
|
|
|||||
ω |
T |
− ∞ |
2 |
π T |
− ∞ |
||
|
|
||||||
23
Aω |
|
1 |
∞ |
|
∞ |
|
|
= |
∫S(t) e jωtdt ; |
S(ω)= |
∫ S(t) e jωtdt |
(2. 8 ) |
|||
|
|
||||||
ω |
π − ∞ |
|
−∞ |
|
|||
Выражение S(ω) (2.8) называется спектральной плотностью сигна-
ла S(t) . Сучетомвышесказанного(2.8) принимаетвид
Aω |
= |
1 |
S(ω) |
( 2.9) |
|
π |
|||
ω |
|
|
||
С точки зрения физического смысла спектральную плотность можно представить как коэффициент пропорциональности между длиной мало-
го интервала частот |
ω и отвечающей ему амплитудой гармонического |
сигналасчастотой ω0 |
лежащейвнутри ω. |
Пример 2.2. Найти спектральную плотность прямоугольного импульсаизображенногонарис.2.3а.
Используясоотношение(2.8) имеем:
|
|
|
∞ |
|
|
τ/ 2 |
|
|
τ/ 2 |
+ j sin ωt)dt |
|
|||||
S(ω) = |
|
∫ U e jωtdt |
|
∫ U e jωtdt |
= U ∫(cosωt |
= |
||||||||||
|
|
−∞ |
|
− τ/ 2 |
|
|
− τ/ 2 |
|
|
|
|
|
|
|||
|
τ/ 2 |
|
τ/ 2 |
|
|
|
|
τ/ 2 |
|
2U |
|
|
τ |
|
||
= U |
∫cos(ωt)dt + |
∫ j sin(ωt)dt = 2U |
∫cos(ωt)dt = |
|
|
sin |
ω |
|
|
|||||||
|
ω |
2 |
||||||||||||||
|
− τ/ 2 |
|
− τ/ 2 |
|
|
0 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
Пусть ξ = |
ωτ |
|
, тогда |
S(ξ) = |
U τ |
sin ξ |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
ξ |
|
|
|
|
|
|
|
|||||
График нормированной спектральной плотности |
S(ξ) |
|
представлен |
|||||||||||||
нарис.2.3б.
24
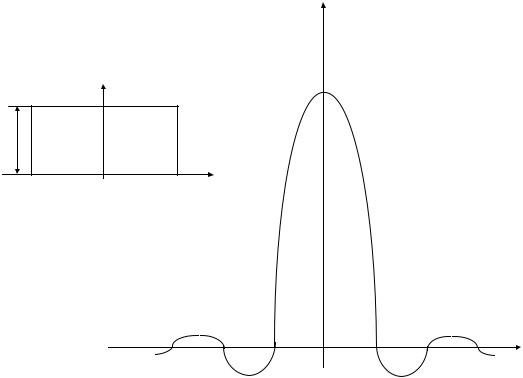
S(ξ)/S(0)
S
U
t
-τ/2 |
a) |
τ/2 |
-π |
π |
ξ |
-2π |
|
2π |
|
б) |
|
Рис.2.3 Cпектральнаяплотностьпрямоугольногосигнала: а- форма ипараметрыпрямоугольногосигнала; б– графикнормированнойспектральнойплотности
25
3.Случайныесигналыишумы
3.1Математическийаппаратслучайныхсигналов
Раздел математики - теория вероятности, исследует случайные процессы. Отличительной чертой случайного процесса является то, что его значения (например: напряжение или ток) нельзя заранее предсказать. Поэтому, когда говорят о конкретной величине какого-нибудь случайного процесса (например: напряжение на зажимах разогретого до температуры
Трезистора), топодразумеваютегостатистическуюхарактеристику.
Втеориивероятностейвведеныпонятия:
-функции распределения случайной величины F(x) , т.е. вероятность
того, что случайная величина x из множества X примет значение, равноеилименьшеечем x0 . F(x) = P(xi ≤ x0 )
Дляфункциираспределениясправедливыдвапредельныхравенства:
F ( −∞ ) = 0 F (+ ∞)=1 (3.1)
- производная от функции распределения - есть плотность вероятности:
|
P(x)= |
dF(x) |
. |
|
(3.2) |
|
|
|
|||
|
|
dx |
|
|
|
Плотностьвероятностиудовлетворяетусловиюнормировки, |
|||||
∑Pi =1 |
т.е. |
∞∫ P(x)dx =1 |
(3.3) |
||
i |
|
|
|
− ∞ |
|
Дляслучайныхвеличин x измножества X введеныпонятия:
•Математическое ожидание ( m ) - среднее значение, которое может приниматьслучайнаявеличина x :
26
_ |
|
∞ |
(3.4) |
m = x |
= |
∫ xP(x)dx |
−∞
•Дисперсия или среднеквадратичное отклонение (δx )2 , которое характеризует меру разброса результатов испытаний относительноматематическогоожидания.
∞
δ2x = ∫ (x − m)2 P(x)dx (3.5)
− ∞
Пример1 Равномерноераспределение.
Пусть случайная величина x может принимать значения из интервала xi ≤ x ≤ x2 , причем вероятности попадания в любые внутренние интервалы равны.
|
|
|
|
|
|
|
|
0, x |
< x1 |
|
|
|
|
|
|
|
|
P(x)= |
1 |
|
, x ≤ x ≤ x |
|
|
|
|
|
2 |
||
|
|
1 |
|||
|
x2 − x1 |
|
|||
|
|
|
|
|
|
|
|
0, x |
> x |
|
|
|
|
|
2 |
|
|
Функцию распределения находят путем интегрирования плотности вероятности.
|
|
|
|
|
|
|
|
|
|
0, x < x1 |
|||
xТЕК |
|
x |
− x1 |
|
||
F(x) = |
∫ P(x)dx = |
, x1 ≤ x ≤ x2 |
||||
|
|
|||||
− ∞ |
x2 |
− x1 |
||||
|
|
|
|
x > x2 |
||
|
|
1, |
||||
|
|
|
|
|
|
|
График плотности вероятности и функции распределения показан на рис.3.1.
27
