dsd11-12 / dsd-11=ТКС / full

тогда фаза зависит от "нулей" передаточной функции как:

Из диаграммы Боде видно, что для нахождения ωс требуется найти экстремум функции фазы от частоты:

Преобразуя уравнение, выразим ωс:

Таким образом если сопоставим выражения (2.6) и (2.8) для максимального запаса по фазе получим:

198

Теперь из выражений для передаточной функции системы выразим номиналы элементов фильтра:

Выше приведённый вывод заимствован из литературы и зарубежных статей [6],[7],[8]. При выводе зависимости для запаса по фазе для упрощения вычислений был опущен коэффициент 2π, который может быть легко восстановлен при необходимости. Данный метод хорошо подходит для моделирования в системах автоматического проектирования. Для более лёгкого понимания работы системы 3-его порядка далее приведём упрощение полученных выражений. Из анализа долговременной стабильности системы и из практики проектирования ФАПЧ выведено следующее соотношение для емкостей фильтра:

Передаточную функцию фазо-частотного детектора со схемой формирования заряда можно записать в следующем виде:

199

Будучи схемой с ОС, ФАПЧ теоретически никогда не достигнет устойчивости, но непрерывно асимптотически к нему стремится. Поэтому под временем захвата обычно понимают время достижения устойчивости с некоторым

относительная ошибка настройки ФАПЧ. В результате приведённых вычислений мы определили, что время захвата ФАПЧ зависит от двух основных параметров ωn и ξ . Исходя из этого, можно приступить к рассмотрению методов уменьшения этого времени, при сохранении хороших фильтрующих свойств системы.

201

8 Применение систем ФАПЧ

ФАПЧ является универсальным блоком, который применяется в различных системах:

-частотный синтезатор, используемый в телевидении, радио или коммуникационных системах с выборкой различных каналов;

-демодуляция (детектирование) модулированных сигналов;

-восстановление тактового сигнала (счетчика) в коммуникационных

ицифровых системах.

8.1Синтезатор частот с ФАПЧ

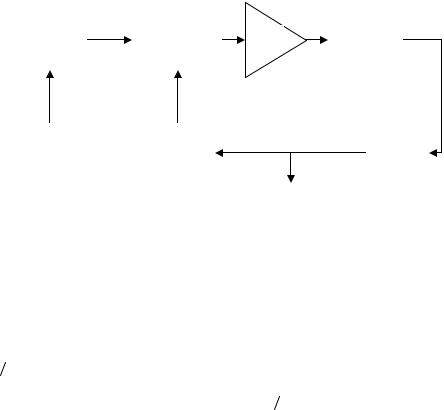
Схема ФАПЧ может быть использована для формирования прецизионного набора частот, путем деления частоты кварцевого генератора. Структурная схема устройства имеет вид, показанный на

fVCO = fOUT

Рис.8.1 Структурная схема синтезатора частот

рис.8.1. Частота кварцевого генератора делится на целое число М делителем частоты, на выходе которого вырабатывается сигнал с

Большое количество (сетку) кратных частот можно получить, если делители на M и N сделать программируемыми.

8.2 Детектор частотно-модулированных сигналов

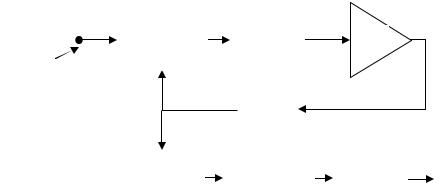
Свойства схемы ФАПЧ позволяют использовать ее в качестве детектора частотно-модулированных сигналов. Структурная схема устройства приведена на рис.8.2. Если ФАПЧ синхронизируется частотно-модулированным сигналом, то управляемый генератор отслеживает мгновенную частоту входного сигнала. Напряжение рассогласования на выходе фильтра UC, которое поддерживает ГУН в режиме синхронизации с входным сигналом, является выходным демодулированным сигналом.

С

Uout

Рис.8.2 Структурная схема частотного детектора

Когда произошел захват частоты схемой ФАПЧ, то справедливо соотношение:

fIN = fVCO

205

где

fVCO = fVCO0 + KVCOUC .

Тогда для напряжения, которое подается на ГУН, будем иметь:

Пусть мгновенное значение частотно модулированного сигнала составляет:

Это напряжение представляет собой модулирующее напряжение, которое накладывается на несущую частоту в передатчике. Как видно из выражения (8.4), модулирующее напряжение имеет два переменных

fM > 3 f1 , то частотно модулированный сигнал ослабится фильтром низкой частоты. В соответствии с этим получим:

( fM f )max ≈ KPD fM KVCO f1 = ( fC )2

Таким образом, модулирующее напряжение можно получить на входе ГУН и отделить от постоянной составляющей посредством конденсатора. Отметим, что в этом случае ФАПЧ объединяет в себе две

206

функции: селекции и демодуляции. Линейность демодулированного выходного сигнала определяется характеристиками ГУНа ( KVCO ).

8.3 Детектор амплитудно-модулированных сигналов

Использование схемы ФАПЧ для демодуляции амплитудномодулированных сигналов показано на рис.8.3. Устройство эффективно при демодуляции сигналов, которые передаются с уменьшенным уровнем несущих колебаний. Схема ФАПЧ с петлей обратной связи производит захват сигнала и восстановление несущей частоты. Далее сигнал с ГУН, через фазосдвигающие цепи подается на выходной детектор, где производится демодуляция амплитудно-модулированного сигнала.

Рис.8.3 Структурная схема АМ детектора

207

8.4Синхронизация и восстановление сигналов тактовых импульсов

Всистемах передачи цифровых сигналов информация в последовательном коде передается по каналу связи. Эта информация может быть цифровой или представлять собой цифровой эквивалент аналоговой информации, как это имеет место при импульсно-кодовой модуляции. При декодировании информации рекомендуется использовать системы ФАПЧ, так как требуется получить неискаженный тактовый сигнал той же частоты что и поступающая информация. Фильтр нижних частот может устранить шумы и наводки, но не отследить медленные изменения скорости передачи информации.

Возможны два различных принципа передачи цифровых данных, а именно прямая передача и передача, модулированная несущей частотой.

Впрямой передаче цифровой сигнал непосредственно проходит по связи. Когда используют систему с несущей частотой, это соответствует передаче цифрового сигнала, модулированного несущим сигналом, как правило, высокой частоты. Используют амплитудную (АМ), частотную (FM), фазовую (РМ) модуляцию или комбинируют различную технику модуляции, например АМ+РМ. В системах с несущей частотой различные цифровые сигналы модулируют на разные несущие частоты. Следовательно, полоса пропускания такой системы должна быть значительно шире, чем полоса пропускания системы прямой передачи.

208