dsd11-12 / dsd-11=ТКС / full

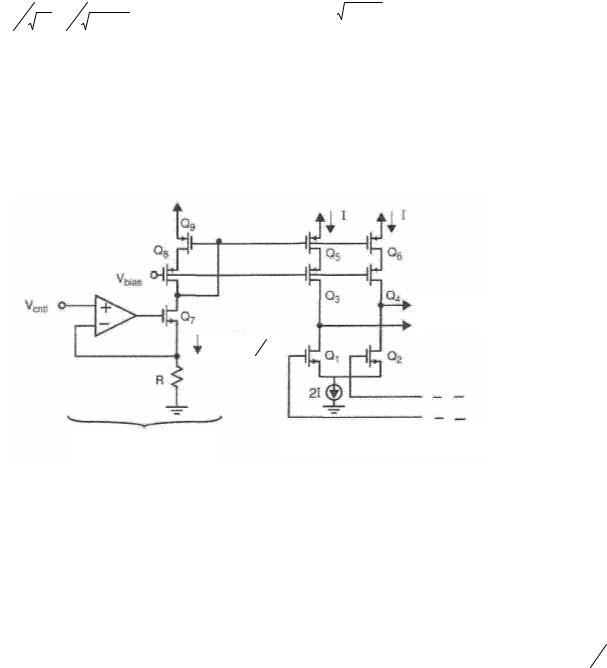
1 IB ≈ 1 UCNTRL , и соответственно fVCO ≈ VCNTRL . Таким образом, отношение

между частотой генерации и управляющим напряжением не линейно, но для многих ГУН эта нелинейность не проблема. Основной недостаток нелинейности это повышение частоты, из-за изменения амплитуды напряжения на выходах каждого каскада при увеличении IB . Если стабилизировать амплитуду выходного напряжения, то линейность возможна.

IR = UCNTRL R

Первый инвертор кольцевого генератора

Схема управления

Рис.7.37. Схема управления.

Схема, показанная на рис.7.37 может быть использована для реализации преобразователя, управляющего источником тока в дифференциальном инверторе кольцевого генератора. Высокий коэффициент ОУ гарантирует, что его дифференциальное входное напряжение очень мало и поэтому напряжение на резисторе R почти равно UCNTRL. Тогда ток через R определяется IR = UCNTRL R .

Этот ток отражается в токовом зеркале, составленном на Q8, Q9 во входной цепи и Q3, Q5 для одного выхода источника тока и Q4, Q6 для второго выхода источника тока. Расчет токового зеркала рассматривался в курсе аналоговых ИС.

188

диапазона, очень строгие требования накладываются на спектральную чистоту локальных генераторов. Работы по моделированию дрожания и фазовому шуму в ГУН, а также попытки улучшить характеристики фазового шума привели к большому числу интегральных конфигураций LC генераторов. Однако проектирование и оптимизация интегральных LC генераторов все ещё ставит много задач проектировщикам схем, поскольку требуется одновременная оптимизация многочисленных переменных и интегральная реализация индуктивностей.

а)

189

б)

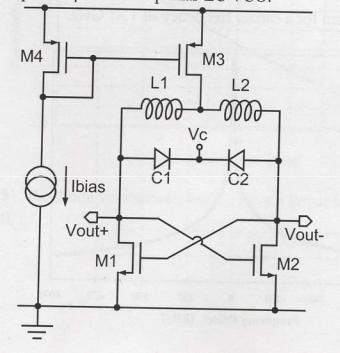
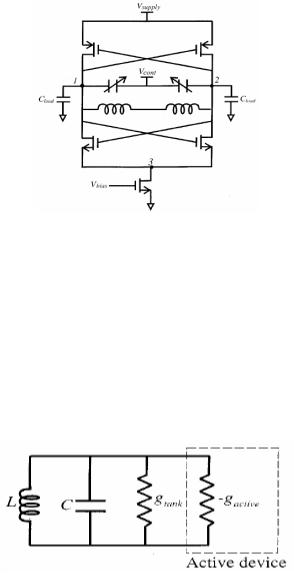
Рис. 7.38 Варианты реализации схемы LC генератора

На рис. 7.38 показан пример реализации LC генератора. Настройка схемы заключается в оптимизации фазового шума. Типовое значение фазового шума у LC генераторов на 20dB лучше, чем у кольцевых и релаксационных.

Рис. 7.39 Модель LC-генератора в установившемся состоянии.

На рис. 7.39 показана модель для LC генератора в установившемся состоянии, где gtank представляет потери в колебательном контуре и -gacitve - эффективная отрицательная проводимость активных элементов, которые компенсируют потери в колебательном контуре. Для типичного LC генератора могут быть определены два режима работы: с ограничением по току или по напряжению. В токоограничивающем режиме амплитуда колебательного контура Vtank растет по линейному закону при возрастании тока смещения Vtank=Ibais/gtank, пока генератор не попадает в режим, ограниченный

190

напряжением. В режиме, ограниченном напряжением, амплитуда ограничена Vlimit и определяется напряжением питания и/или падением в рабочем режиме на активных элементах (например, МОП транзисторах). Таким образом, Vtank может быть выражено как

Используя индуктивность колебательного контура L как независимую переменную, определим Ibias. Энергия колебательного контура Etank определяется как

Тогда Vtank может быть выражено через Etank, то есть.

где, ω0 =1/ LC - частота колебаний. Амплитуда колебательного контура растет с ростом L для данного Etank и ω0 . Таким образом, пока текущим режимом является токоограниченный, его можно описывать как режим с ограниченной индуктивностью, где L - независимая переменная.

Тогда Vtank переписывается как

Эквивалентная модель схемы генератора показана на рис.7.40. Модель симметричной спиральной индуктивности с одинаковыми RC нагрузками на обоих концах (рис.7.41) используется как часть модели колебательного контура.

191

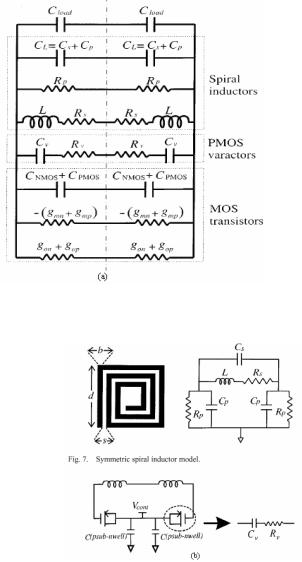
Рис. 7.40 Эквивалентная модель генератора

Рис. 7.41 Модель симметричной спиральной индуктивности и LC

колебательного контура с MOSCAP варакторами.

Имеются двенадцать начальных переменных, по которым выполняется оптимизация генератора: размеры МОП транзисторов (Wn, Ln, Wp и Lp), геометрические параметры интегральных спиральных катушек индуктивности (ширина металла b, расстояние между витками металла s, число витков n, и диаметр d), максимальные и минимальные значения варакторов (Cv,max и Cv,min), емкость нагрузки (Cload) и остаточный ток смещения в ядре генератора

(Ibias).

192

Часто фигурирующие параметры в оптимизации это: потери gtank, эффективная отрицательная проводимость –gactive, индуктивность колебательного контура Ltank, и емкость колебательного контура Ctank из рис. 7.39. Они задаются следующими выражениями

где gl и gv эффективные параллельные проводимости индуктивностей и варакторов, соответственно.

Проектные ограничения налагаются на фазовый шум (это есть главная цель оптимизации), утечку мощности, амплитуду колебательного контура, ширину настраиваемого диапазона, условия запуска и диаметр спиральной индуктивности.

Во-первых, ограничение на максимум мощности налагается в виде максимума тока смещения Imax источника напряжения питания, т.е.

(7.61)

Во-вторых, амплитуда колебательного контура должна быть большей, чем Vtank,min, чтобы обеспечить достаточный размах напряжения для следующего каскада:

В-третьих, диапазон настройки частоты генератора должен быть такой, чтобы был запас некоторого минимального процента от входящей частоты ω, то есть:

193

высокие параметры синтезаторов. Основной принцип их работы заключается в применении переменного целого коэффициента деления в течение некоторого периода. Результатом является средневзвешенный коэффициент, имеющий дробные значения. Однако подобные делители вносят дополнительные периодические шумы в спектр выходного сигнала.

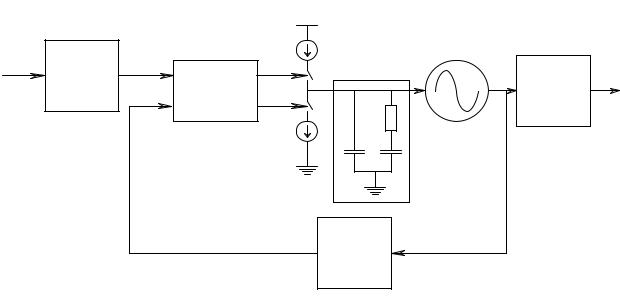
7.12. Основные зависимости системы ФАПЧ.

Известно, что порядок системы с обратной связью определяется максимальной степенью s в знаменателе передаточной функции для закрытой цепи. Таким образом, для любой ФАПЧ порядок определяется фильтром низких частот. Типичное значение порядка фильтра для ФАПЧ синтезаторов частоты два. Следовательно, для нахождения основных зависимостей нам требуется рассмотреть систему третьего порядка.

F(s)

Рис. 7.42 Структура ФАПЧ с пассивным фильтром второго порядка.

Рассмотрим обобщённую систему ФАПЧ с пассивным фильтром второго порядка. Передаточная функция фильтра может быть записана как:

195

или после преобразования:

Подставляя полученное выражение в уравнение для линеаризованной передаточной функции ФАПЧ, получим:

196

-40 dB/dec

|G(s) H(s)|

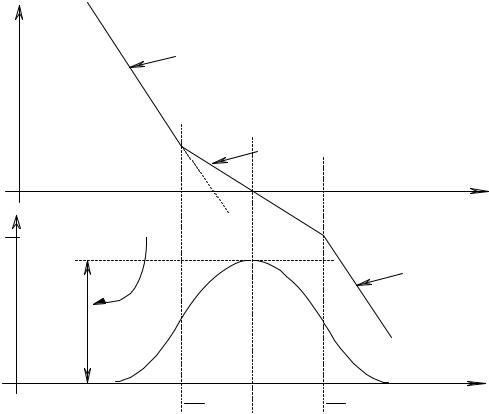
Рис 7.43 Диаграмма Боде для передаточной функции ФАПЧ.

На рисунке 7.43 изображена диаграмма Боде полученной передаточной функции. На низких частотах спад АЧХ в -40 децибел на декаду обусловлен наличием двух интегрирующих цепочек в составе ФАПЧ. Они связанны с фильтрующими свойствами ГУН и схемы накачки заряда (Charge Pump). Частоты 1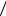τ1 и 1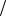τ2 выбираются так, чтобы запас по фазе системы был максимален. Частота ωс, при которой наблюдается максимум запаса по фазе, есть некая характеристическая частота "единичного усиления" системы, фактически определяет ширину полосы пропускания ФАПЧ. Для нахождения ωс подставим в выражение для передаточной функции s = jω: