dsd1-10 / dsd-10=Спецглавы проектирования АИС / Эннс / 01.Представление аналоговых сигналов

Лекция 1. Представление аналоговых сигналов

Представление сигналов во временной и частотной областях

Обобщенная синусоида может быть представлена в виде комплексной функции в показательной форме

,

где (рис. 1.1)

,

модуль

,

фаза

.

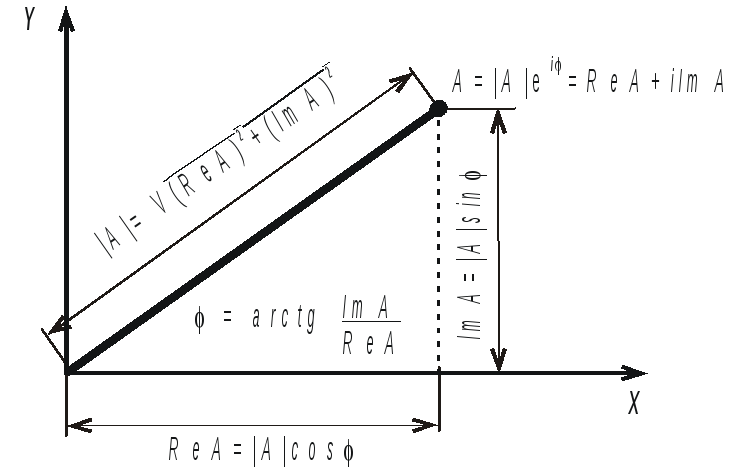
Рис. 1.1. Геометрические соотношения между составляющими комплексного числа А

Сигнал произвольной формы обычно содержит непрерывный спектр частот, т.е. интервал по частоте между соседними гармониками равен бесконечно малой величине, а число гармонических составляющих бесконечно велико. В качестве элементарной составляющей сигнала в этом случае принимается не синусоида , а ее приращение , где – бесконечно малое приращение частоты. Последнее выражение можно рассматривать как обычную синусоиду частоты , локализированную в полосе частот , с бесконечно малой комплексной амплитудой . Сумма достаточно большого числа таких синусоид различных частот позволяет аппроксимировать широкий класс функций времени (включающий все функции описывающие физические процессы). Заменяя сумму синусоид интегралом по всей совокупности частот, функция может быть представлена в виде

. (1.1)

Для преобразования (1.1), которое называется обратным, существует единственное прямое преобразование

,

т.е. каждой функции однозначно соответствует функция и наоборот.

Полученные интегральные соотношения – пара преобразований Фурье

.

называется комплексной спектральной плотностью или спектром сигнала . Таким образом, во временной области сигнал характеризуется функцией времени , а в частотной (или области изображений) – спектром .

Например, спектр прямоугольного импульса (рис. 1.2)

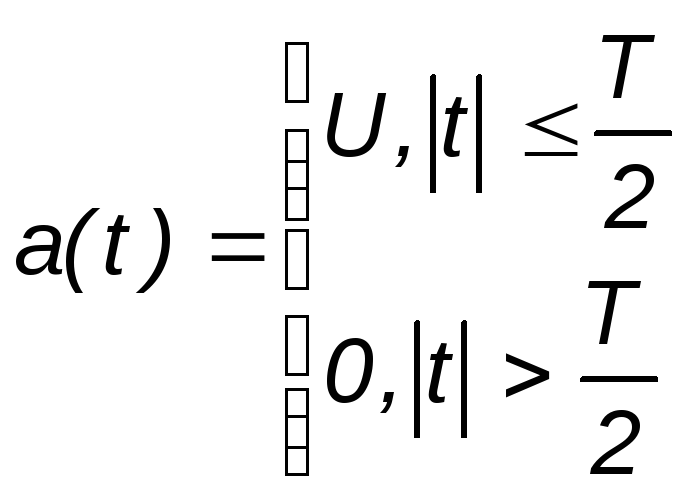
описывается выражением (рис. 1.3)

.

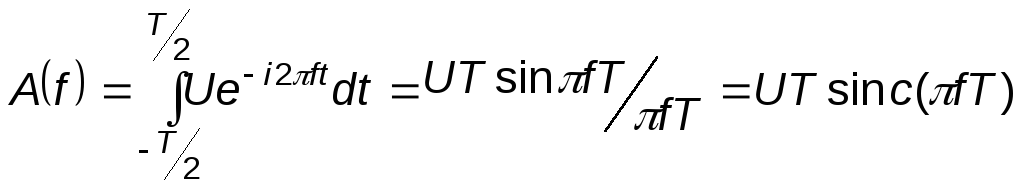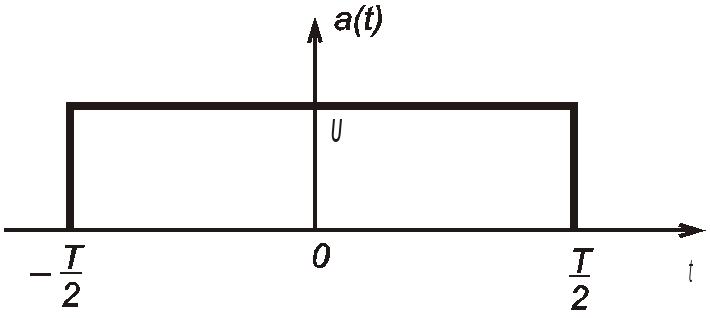
Рис. 1.2. Прямоугольный импульс

Рис. 1.3. Спектральная плотность прямоугольного импульса

Д

f

искретные сигналы

Сигнал, непрерывный по уровню и по времени называется аналоговым. Дискретный по времени сигнал описывается функцией, которая определена в дискретные моменты времени. Дискретный по времени сигнал, квантованный по уровню, называется цифровым.

Дискретный по времени сигнал может быть представлен как

,

где – исходный аналоговый (дискретизируемый) сигнал;

– дискретизирующий периодический сигнал с частотой повторения f_s (разложение в ряд Фурье). – комплексная амплитуда k–ой гармоники. Таким сигналом может быть последовательность – импульсов или прямоугольных и иных импульсов.

.

Спектр дискретного сигнала (рис. 1.4)

.

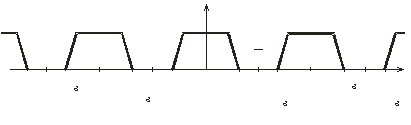
Рис. 1.4. Спектры сигналов: а – исходного аналогового; б – дискретного, с частотой дискретизации выше частоты Найквиста, ; в – дискретного, с

На рис. 1.4 показан спектр дискретного сигнала для случая дискретизации в виде последовательности δ-импульсов. При дискретизации в виде прямоугольных импульсов смещенные копии спектра умножаются на коэффициенты, определяющие взвешивание с помощью функции sinc(x).

Удвоенная верхняя частота спектра аналогового сигнала определяется как частота Найквиста. Частота дискретизации должна быть не меньше частоты Найквиста. В противном случае наблюдается эффект наложения спектров. Для того, чтобы избежать эффекта наложения спектров, требуется выполнить условие, известное как теорема отсчетов или теорема В.А.Котельникова

,

где – частота дискретизации; – верхняя граничная частота аналогового сигнала.

Частотно–временные характеристики системы

Единичная импульсная функция или дельта-функция – равна «0» при , при обращается в , причем площадь, ограничиваемая дельта-функцией равна 1. Амплитудный спектр -функции равен 1, т.е. значение амплитудного спектра на любой частоте равно 1.

Воздействие импульса на вход системы эквивалентно воздействию бесконечного множества одинаковых по амплитуде синусоид всех возможных частот.

Реакция системы на единичную импульсную функцию – импульсная переходная функция – характеризует систему во временной области.

Передаточная функция

.

– описывает свойства цепи в частотной области.

Реакция цепи f(t) с импульсной переходной функцией на входное воздействие описывается уравнением

,

которое называется сверткой (интегралом Дюамеля).

Обозначение свертки

,

Если , то

.

В произвольном случае, если представить g(t) в виде последовательности импульсов, то – сумма реакций на каждый входной импульс.

Если спектральная плотность входного сигнала , передаточная функция , то спектральная плотность выходного сигнала , т.е. спектр выходного сигнала равен произведению спектра входного сигнала на передаточную функцию цепи.

Применение преобразования Лапласа для анализа

аналоговых цепей

Для анализа аналоговых цепей используется преобразование Лапласа. Его применение обусловлено просто­той решения линейных дифференциальных уравнений, которые, в свою очередь описывают работу аналого­вых устройств. Одностороннее преобразование Лапласа определяется выраже­нием

,

где – комплексная переменная.

Обратное преобразование Лапласа определяется как

,

где – контур на s–плоскости, охватывающей все особые точки Y(s).

Существует соответствие между преобразованием Лапласа и преобразованием Фурье. Если Y_B(s) – двустороннее преобразование Лапласа функции , то преобразованием Фурье A() функции будет

.

Исследование свойств аналоговых цепей, в частности определение устойчивости, удобно проводить с использованием передаточной функции H(s).

Передаточная функция H(s) системы, на вход которой подается сигнал x(t), вызывающий реакцию на выходе y(t), за­дается выражением

,

где и – нули и полюсы системы; – вещественный мно­житель.

Полюсы передаточной функции определяют собственные колебания системы, так как, в соответствии с обратным преобразованием Лапласа, выходной сигнал описывается линейной комбинацией экспоненциальных функций . характеризует скорость затухания гармонических колебаний, – их круговую частоту. Расположение полюсов определяет устойчивость системы. Система устойчива, если полюсы передаточной функции располагаются в левой полуплоскости, то есть и функция убывает при .

АЧХ системы представляет собой зависимость модуля передаточной функции от частоты

.

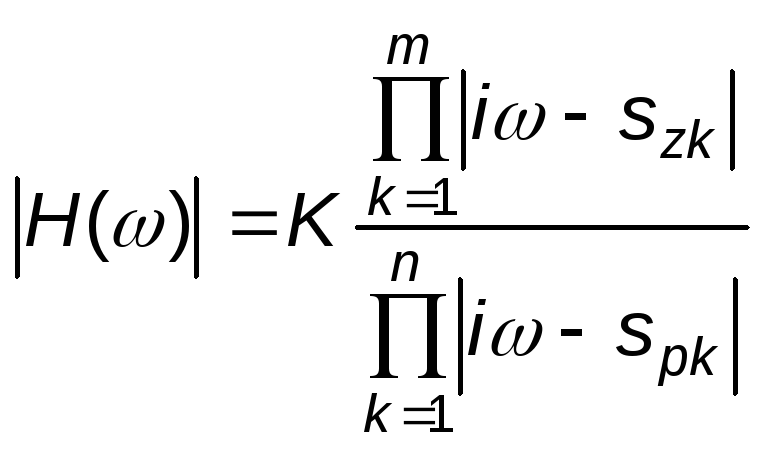ФЧХ выражает зависимость аргумента передаточной функции от частоты

.

Вид карты нулей и полюсов аналоговой системы изображен на рис. 1.5.

Рис. 1.5. Карта нулей и полюсов аналоговой системы