dsd1-10 / dsd-10=Спецглавы проектирования АИС / Эннс / 02.z-преобразование

Лекция 2. Применение z–преобразования для анализа дискретных цепей.

Для анализа дискретных цепей используется z–преобразование, определяемое выражением (одностороннее преобразование)

, (2.1)

где представляет собой последовательность выборок сигнала, взятую в дискретные моменты времени 0, T, 2T, …, nT; .

Комплексную переменную z можно представить в полярных координатах или для частного случая : . В этом случае выражение (2.1) принимает вид

.

Оператор соответствует единичной задержке в последовательности дискретных выборок во временной области.

Дискретная система, на вход которой подается воздействие и реакция которой (выходной сигнал) , описывается передаточной функцией

,

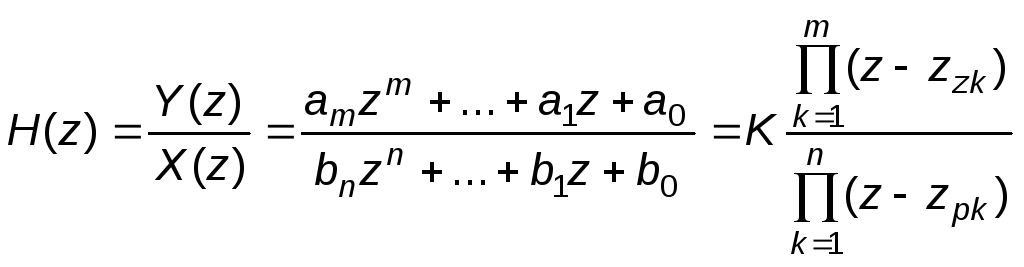где – вещественный коэффициент; и – нули и полюсы соответственно.

Частотная характеристика системы определяется заменой z на . В результате АЧХ можно представить в виде

.

ФЧХ системы

.

на плоскости представляет собой окружность единичного радиуса с центром в начале координат.

Пример карты нулей и полюсов дискретной системы приведен на рис. 2.1.

Рис. 2.1. Карта нулей и полюсов дискретной системы

В соответствии с z–преобразованием импульсная характеристика представляет собой линейную комбинацию функций вида . Система будет устойчивой, если , то есть если все ее полюсы лежат внутри единичной окружности.

Соотношения между характеристиками аналоговых и дискретных цепей

Используя различные правила можно установить соотношения между комплексной переменной передаточной функции аналоговой системы и комплексной переменной передаточной функции дискретной системы z. Установленные формальные соотношения, как правило, соответствуют конкретным схемотехническим реализациям элементов дискретных аналоговых цепей.

При использовании обратной разности

или .

При использовании прямой разности

или .

Билинейное преобразование

или .

Отображения комплексных переменных с помощью билинейного преобразования показано на рис. 2.2.

Ось плоскости отображается в окружность единичного радиуса на плоскости .

Дискретная и аналоговая частоты и при билинейном преобразовании связаны соотношением (рис. 2.3)

,

При высокой частоте дискретизации, все три вида преобразования приводят к одному результату, который соответствует методу прямой разности

.

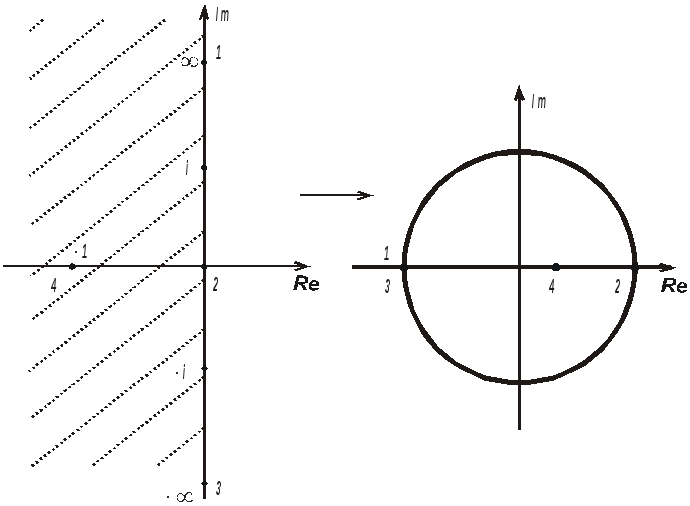
Рис. 2.2. Отображения комплексных переменных с помощью билинейного преобразования

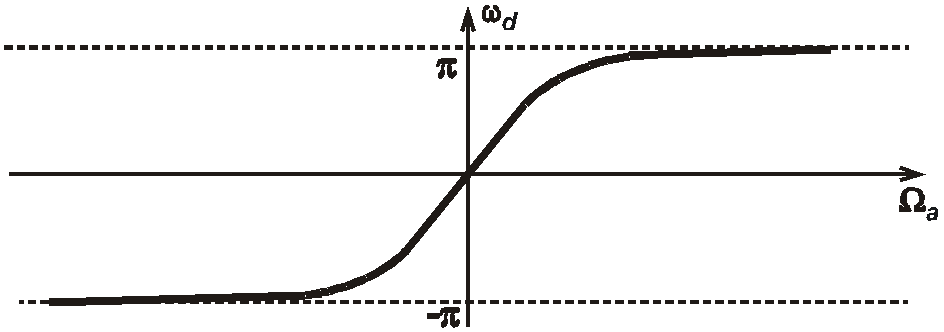
Рис. 2.3. Связь дискретной и аналоговой частот при билинейном преобразовании

Передаточная функция звена второго порядка в s–области может быть записана в виде

где , ; , – резонансная частота и добротность полюса.

Передаточная функция звена второго порядка в z–области имеет вид

где , .

Соотношения между параметрами звеньев в s и z–областях приведены для высокой частоты дискретизации и большой добротности (рис. 2.4)

,

,

,

,

,

.

Рис. 2.4. Соотношения между полюсами передаточной функции звена второго порядка в s– и z–областях