Практическая часть

В этой лабораторной работе мы рассмотрим дифференциальные уравнения второго порядка и построим фазовые плоскости для шести возможных корней дифференциального уравнения, используя программу MatLab.

Дифференциальное уравнение второго порядка имеет вид:

Заменим вторую произвольную на , после чего получим систему уравнений:

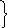
Так как у нас даны корни решения характеристического уравнения, а само характеристическое уравнение имеет вид:

получается

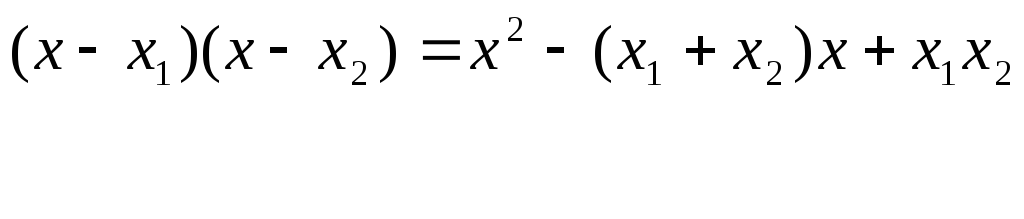
Получив значения и , мы можем построить фазовую плоскость для данного дифференциального уравнения.

Рассмотрим пример выполнения лабораторной работы на варианте 1.

Даны корни i, -1i, 1i, -1 –1, 1 1, -1 1,

В качестве примера рассмотрим первый вариант:

Для первой пары корней получаем = 0, = 1.

Описанная выше система будет иметь вид

Для построения фазовой плоскости для данного дифференциального уравнения воспользуемся файлами программы MatLab ode 23 и vpol. Перед тем, как вносить какие-либо изменения скопируйте эти файлы и переименуйте, чтобы не изменять оригинальные файлы. В файле vpol задайте уравнение. Файла vl (переименованный vdpol) для нашего случая будет иметь вид:

Function yprime = vdpol(t,y);

Yprime = [1.*y(2); y(1)].

После того, как мы описали дифференциальное уравнение необходимо внести изменения в файл ol (переименованный ode 23). Исходная часть файла выглядит так:

t0 = 0;

tfinal = 10;

y0 = [0 1]; % Define initial conditions.

[t,y] = ode23(‘vdpol’, t0, tfinal, y0);

%paus %Strik any key to start ODE23 solution.

tol = 1.e-3; %Accuracy

trace = 1;

[t,y] = ode23(‘vdpol’, t0, tfinal, y0, tol, trace);

%plot(t,y), title(‘van der Pol equation time history’), pause

plot(y(:,1),y(:,2)), title(‘van der Pol equation – phase plane plot’), pause

clc

Но мы должны поставить вместо vpol имя своего файла с описанием дифференциального уравнения.

После этого запустите программу MatLAB и наберите имя файла o1.m

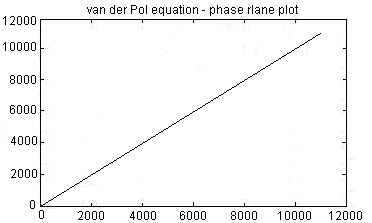
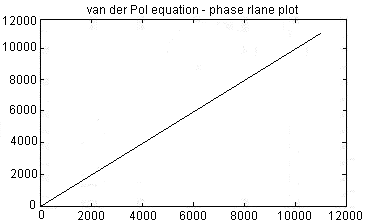
На дисплее отобразится результат: фазовая плоскость, характерная для первого случая.

После построения фазовой плоскости для первой пары корней, постройте фазовую плоскость для второй пары корней и т.д.

У вас должно получиться шесть приведенных ниже фазовых плоскостей:

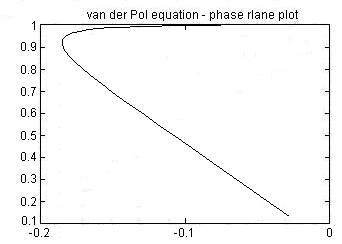
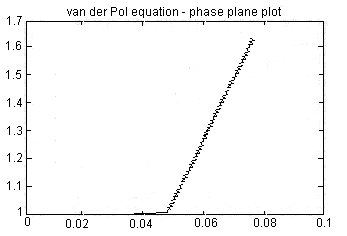
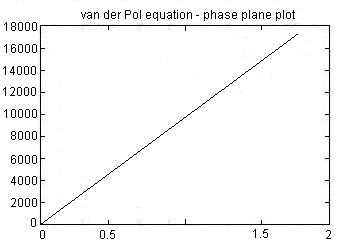
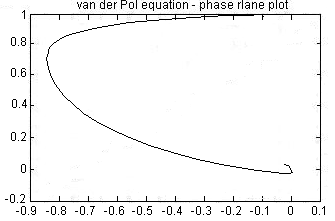
Список вариантов:

№ варианта

1	I	-1I	1I	-1, -1	1, 1	-1, 1
2	2I	-12I	12I	-1, -2	1, 2	-1, 2
3	3I	-13I	13I	-1, -3	1, 3	-1, 3
4	4I	-14I	14I	-1, -4	1, 4	-1, 4
5	1I	-2I	2I	-2, -1	2, 1	-2, 1
6	2I	-22I	22I	-2, -2	2, 2	-2, 2
7	3I	-23I	23I	-2, -3	2, 3	-2, 3
8	4I	-24I	24I	-2, -4	2, 4	-2, 4
9	1I	-3I	3I	-3, -1	3, 1	-3, 1
10	2I	-32I	32I	-3, -2	3, 2	-3, 2
11	3I	-33I	33I	-3, -3	3, 3	-3, 3
12	4I	-34I	34I	-3, -4	3, 4	-3, 4
13	1I	-4I	4I	-4, -1	4, 1	-4, 1
14	2I	-42I	42I	-4, -2	4, 2	-4, 2
15	3I	-43I	43I	-4, -3	4, 3	-4, 3
16	4I	-44I	44I	-4, -4	4, 4	-4, 4
17	1I	-45I	45I	-4, -5	4, 5	-4, 5
18	2I	-5I	5I	-5, -1	5, 1	-5, 1
19	3I	-52I	52I	-5, -2	5, 2	-5, 2
20	4I	-53I	53I	-5, -3	5, 3	-5, 3