МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО
ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Московский государственный институт электроники и математики
(Технический университет)
Кафедра «Вычислительные системы и сети»
НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Методические указания к лабораторной работе 4
Часть 1
Москва 2001
Теоретическая часть
Нелинейной системой автоматического регулирования называется такая система, которая содержит хотя бы одно звено, описываемое нелинейным уравнением.
Различают статические и динамические нелинейности. Первые представляются в виде нелинейных статических характеристик, а вторые – в виде нелинейных дифференциальных уравнений.
Процессы в нелинейных системах автоматического регулирования имеют целый ряд весьма существенных особенностей, которые не встречаются в линейных системах.
Благодаря этим существенным особенностям даже вопрос об устойчивости системы становится здесь более сложным. Кроме структуры системы и значений ее параметров для устойчивости того или иного установившегося процесса имеют значения здесь, в отличие от линейных систем, также и начальные условия. Возможен новый вид установившегося процесса – автоколебания, т.е. устойчивые собственные колебания с постоянной амплитудой при отсутствии внешних колебательных воздействий. Когда в системе возникают автоколебания, то установившееся состояние, соответствующее постоянному значению регулируемой величины, часто становится невозможным.
Следовательно, в общем случае на плоскости параметров системы могут быть не два вида плоскостей (устойчивости и неустойчивости), как в линейных системах, а больше: 1) область устойчивости равновесного состояния с постоянным значением регулируемой величины; 2) область устойчивых автоколебаний; 3) область неустойчивости системы; 4) области, соответствующие другим, более сложным случаям.
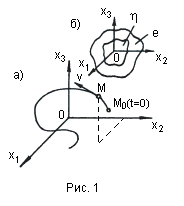
Для наглядного представления о сложных нелинейных процессах регулирования часто прибегают к понятию фазового пространства, которое заключается в следующем. Дифференциальной уравнение замкнутой системы регулирования n-го порядка можно преобразовать к системе n дифференциальных уравнений первого порядка в виде
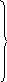
![]()
![]() (1.1)
(1.1)
![]()
с начальными условиями
![]() ,
при t = 0 ,
,
при t = 0 ,
где
![]() переменные, являющиеся искомыми функциями
времени, причем
переменные, являющиеся искомыми функциями
времени, причем
![]() может обозначать регулируемую величину,
а
может обозначать регулируемую величину,
а
![]() – вспомогательные переменные; f
и g
– возмущающее и задающее воздействия.
– вспомогательные переменные; f
и g
– возмущающее и задающее воздействия.
Пусть, например, в
уравнениях (1.1) будет n=3
(система третьего порядка). Переменные
![]() здесь могут иметь любой физический
смысл. Но условно их можно представить
мысленно как прямоугольные координаты
некоторой точки M
(рис. 1, а).
здесь могут иметь любой физический
смысл. Но условно их можно представить
мысленно как прямоугольные координаты
некоторой точки M
(рис. 1, а).
В
реальном процессе регулирования в
каждый момент времени величины
![]() имеют вполне определенные значения.
Это соответствует вполне определенному
положению точки M
в пространстве (рис. 1, а).
имеют вполне определенные значения.
Это соответствует вполне определенному
положению точки M
в пространстве (рис. 1, а).
С
течением времени в реальном процессе
величины
![]() определенным образом изменяются. Это
соответствует определенному перемещению
точки М
в пространстве по определенной траектории.
Следовательно, траектория движения
точки М
может служить наглядной геометрической
иллюстрацией динамического поведения
системы в процессе регулирования.
определенным образом изменяются. Это
соответствует определенному перемещению
точки М
в пространстве по определенной траектории.
Следовательно, траектория движения
точки М
может служить наглядной геометрической
иллюстрацией динамического поведения
системы в процессе регулирования.
Точка
М
называется изображающей
точкой,
ее траектория называется фазовой
траекторией,
а пространство (![]() )
называется фазовым
пространством.
)
называется фазовым
пространством.
Производные во времени от координат точки представляют проекции ее скорости на оси координат. Следовательно, по значениям правых частей уравнений (1.1) в каждый момент времени можно судить о направлении движений изображающей точки М, а вместе с тем и о поведении соответствующей реальной системы в процессе регулирования.
Начальные
условия процесса регулирования (![]() )
определяют координаты начальной точки
фазовой траектории
)
определяют координаты начальной точки
фазовой траектории
![]() (рис.1,
а).
(рис.1,
а).
Если
переменных в уравнениях (1.1) будет всего
две:
![]() и
и
![]() (система второго порядка), то изображающая
точка будет двигаться не в пространстве,
а на плоскости (фазовая
плоскость).
(система второго порядка), то изображающая
точка будет двигаться не в пространстве,
а на плоскости (фазовая
плоскость).
Если переменных будет любое число n>3 (система n-го порядка), то фазовое пространство будет не трехмерным, а n-мерным.
Итак, фазовое пространство и фазовые траектории представляют собой лишь геометрический образ динамических процессов, протекающих в системе. В этом геометрическом представлении участвуют координаты и исключено время. Фазовая траектория сама по себе дает лишь качественное представление о характере поведения системы. Чтобы определить количественно положение изображающей точки (а значит, и состояние системы) в любой момент времени, нужно найти решение заданных дифференциальных уравнений (1.1) во времени.
Если
уравнения (1.1) составлены в отклонениях
от установившегося состояния, то
последнее характеризуется значениями
![]() =
=
![]() =
=
![]() = 0.
Следовательно, изображением установившегося
состояния системы является начало
координат фазового пространства.
= 0.
Следовательно, изображением установившегося
состояния системы является начало
координат фазового пространства.
Отсюда вытекает, что фазовые траектории устойчивой линейной системы будут асимптотически приближаться к началу координат при неограниченном увеличении времени. Фазовые траектории неустойчивой линейной системы будут неограниченно удаляться от начала координат.
Пусть переходный процесс в некоторой системе описывается уравнением второго порядка.
![]() (1.2)
(1.2)
Введем
обозначения для скорости изменения
отклонения регулируемой величины
![]() .
Тогда уравнение системы (1.2) преобразуется
к виду
.
Тогда уравнение системы (1.2) преобразуется
к виду
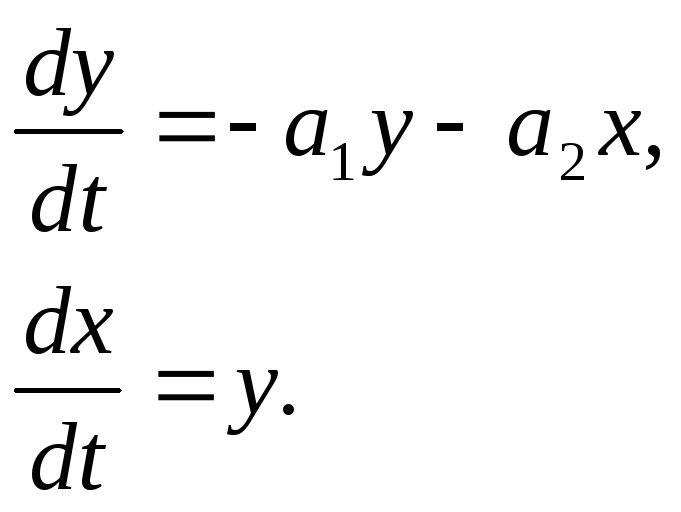
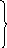 (1.3)
(1.3)
Исключим
из уравнения (1.3) время t,
разделив первое из них на второе (при x
и y
![]() ):
):
![]() (1.4)
(1.4)
Решение этого дифференциального уравнения с одной произвольной постоянной определяет собой некоторое семейство так называемых интегральных кривых на фазовой плоскости (x, y), каждая из которых соответствует одному определенному значению произвольной постоянной.
Вся совокупность интегральных кривых представит собой все возможные фазовые траектории, а значит, и все возможные виды переходного процесса в данной системе автоматического регулирования при любых начальных условиях.
Рассмотрим отдельно различные случаи. Уравнению (1.2) соответствуют корни характеристического уравнения
![]() ,
,
Причем возможны шесть случаев:
-
корни чисто мнимые при
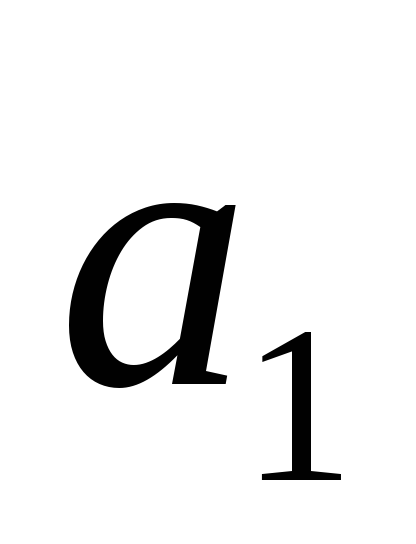 = 0,
= 0,
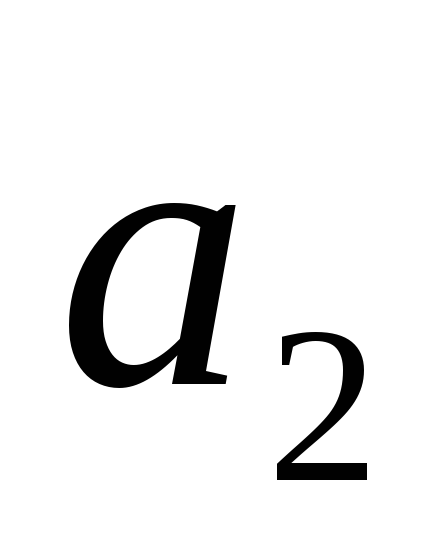 > 0
(граница устойчивости линейной системы);
> 0
(граница устойчивости линейной системы); -
корни комплексные и имеют отрицательные вещественные части при
 < 4
< 4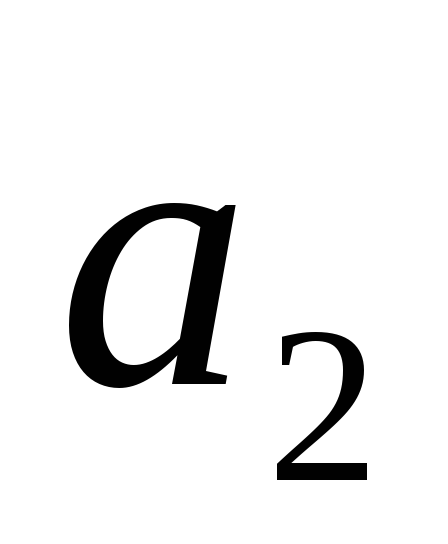 ,
,
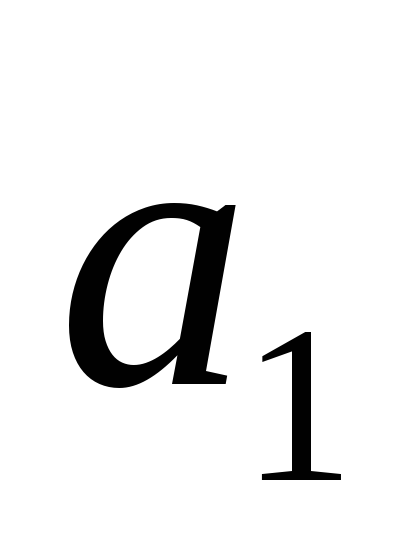 >
0,
>
0,
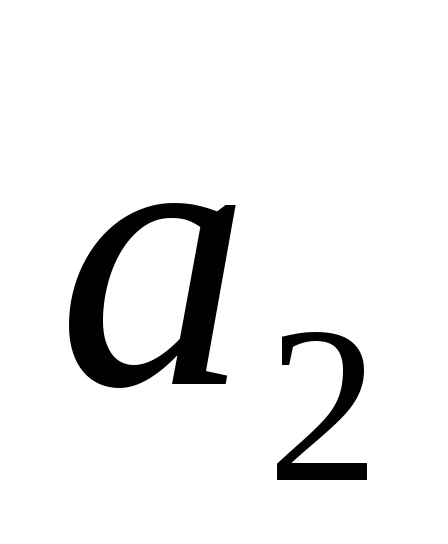 > 0 (устойчивая линейная система);
> 0 (устойчивая линейная система); -
корни комплексные и имеют положительные вещественные части при
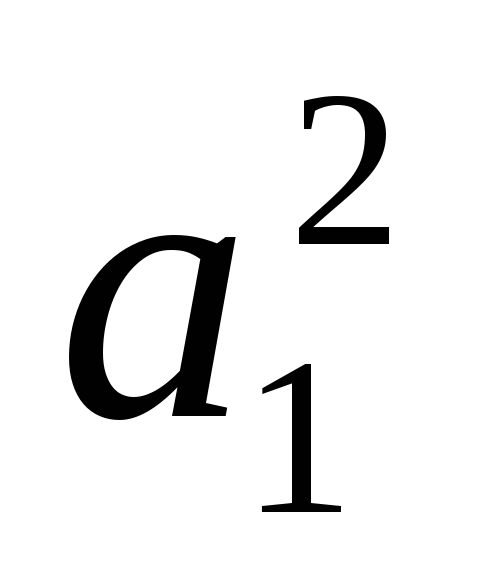 < 4
< 4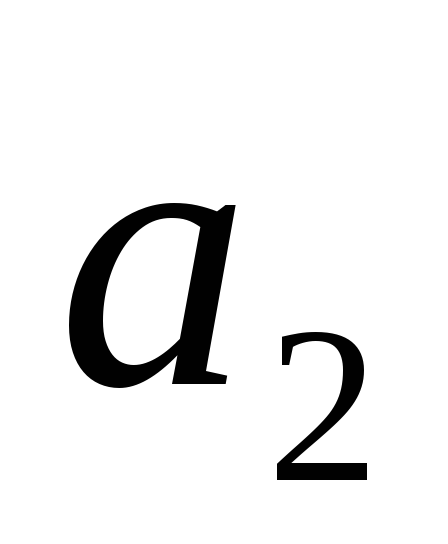 ,
,
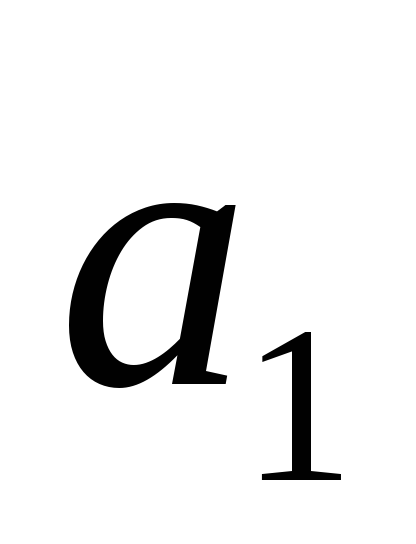 <
0,
<
0,
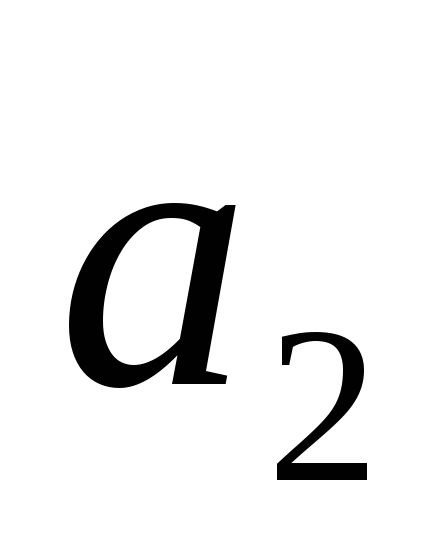 > 0 (неустойчивая линейная система);
> 0 (неустойчивая линейная система); -
корни вещественные отрицательные при
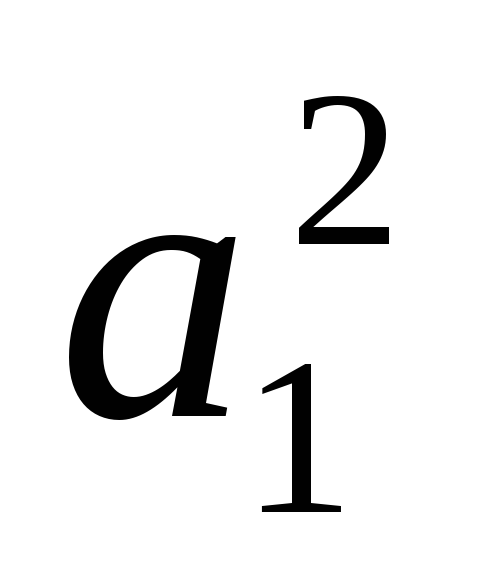 < 4
< 4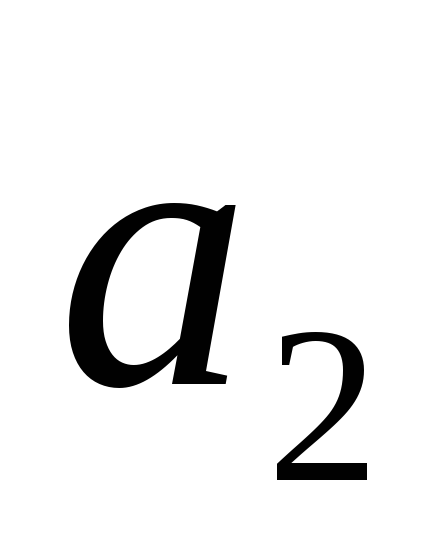 ,
,
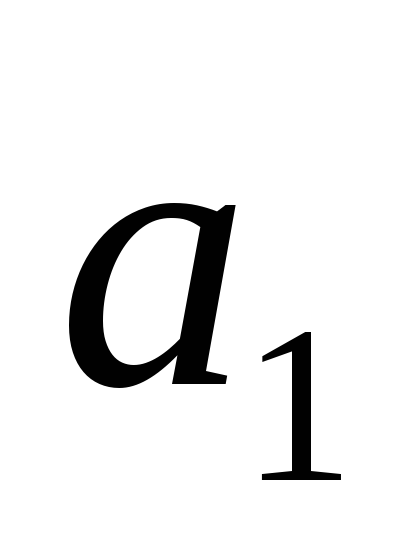 >
0,
>
0,
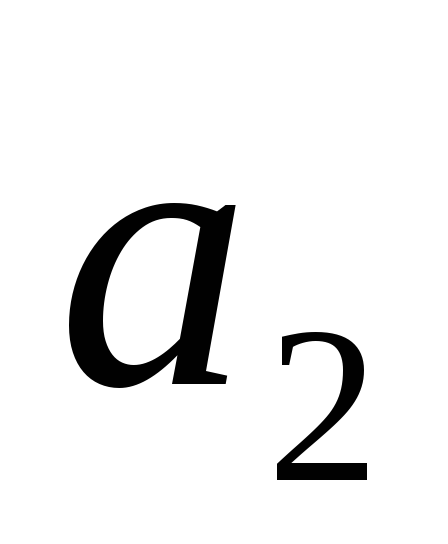 > 0
(устойчивая
линейная система);
> 0
(устойчивая
линейная система); -
корни вещественные положительные при
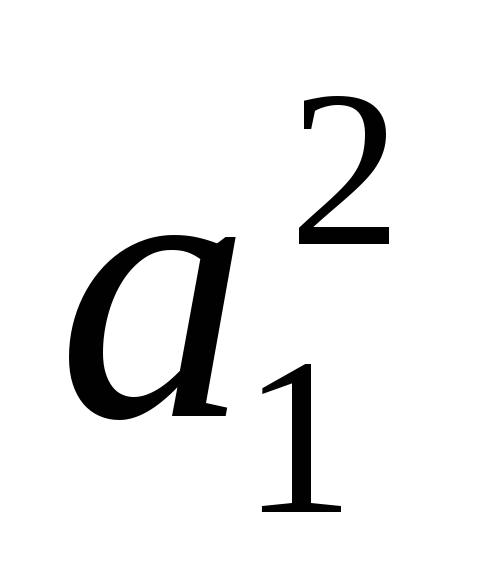 < 4
< 4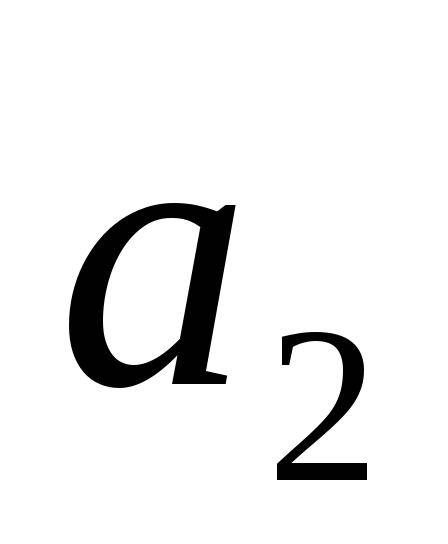 ,
,
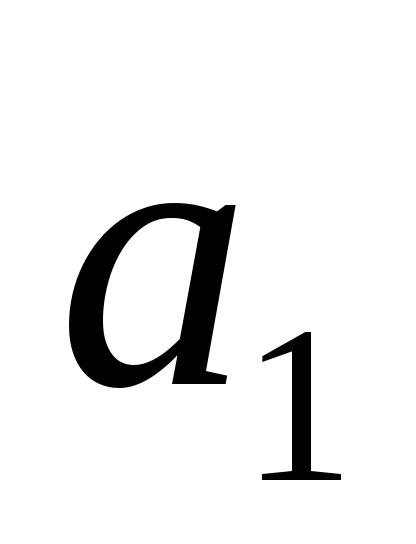 <
0,
<
0,
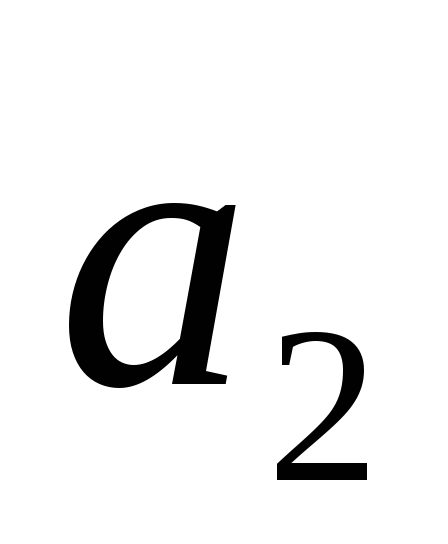 > 0 (неустойчивая линейная система);
> 0 (неустойчивая линейная система); -
корни вещественные и имеют разные знаки при
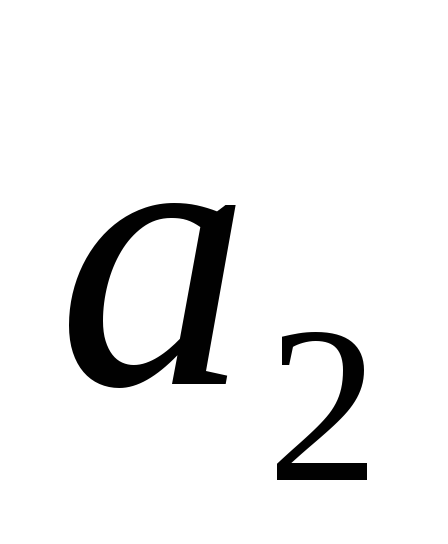 < 0 (неустойчивая линейная система); в
частности, один из корней будет равен
нулю при
< 0 (неустойчивая линейная система); в
частности, один из корней будет равен
нулю при
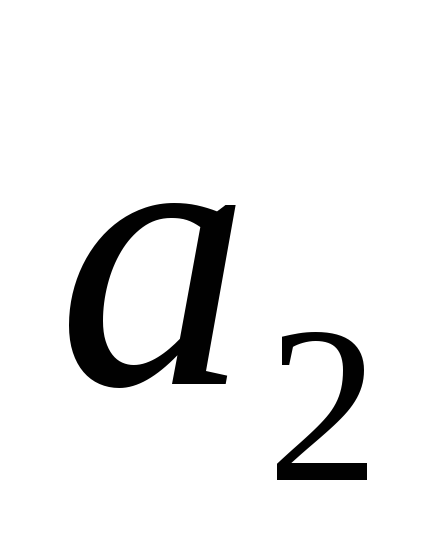 = 0 (граница устойчивости линейной
системы).
= 0 (граница устойчивости линейной
системы).
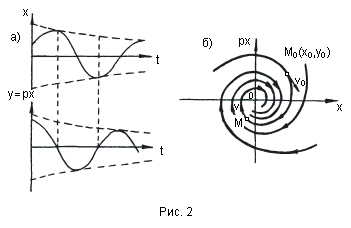
С л у ч а й 1. В первом случае получаются, как известно, незатухающие колебания (рис. 2, а)
![]() ,
,
![]()
![]() (1.5)
(1.5)
с
постоянной амплитудой А и начальной
фазой
![]() ,
которые зависят от начальных условий.
Для фазовой плоскости уравнения (1.5)
представляют собой параметрические
уравнения эллипса с полуосями А и
,
которые зависят от начальных условий.
Для фазовой плоскости уравнения (1.5)
представляют собой параметрические
уравнения эллипса с полуосями А и
![]() (рис.2,б). Уравнение эллипса
(рис.2,б). Уравнение эллипса
![]()
можно
получить непосредственным решением
дифференциального уравнения фазовых
траекторий (1.4) при
![]() =
0 и
=
0 и
![]() =
=![]() ,
причем А – произвольная постоянная
интегрирования.
,
причем А – произвольная постоянная
интегрирования.
Итак, периодическим колебаниям системы (рис. 2,б) соответствует движение изображающей точки по замкнутой кривой (рис.2,б).
С л у ч а й 2. В этом случае (комплексные корни с отрицательными вещественными частями), как известно, имеют место затухающие колебания (рис.3,а)
![]() ,
,
![]() ,
,
где
![]() ,
,
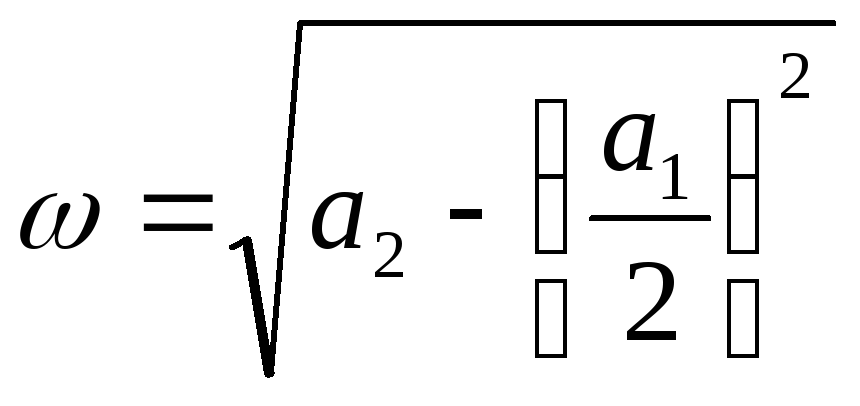 ,
,
![]() ,
,
![]() ,
,
а
произвольные постоянные А и
![]() определяются
из начальных условий:
определяются
из начальных условий:
![]() =
x
y
=
=
x
y
=
![]() =
=
![]() при
t=0.
при
t=0.
Значения
x и y не возвращаются за период колебания
к прежним, а становятся меньше. Это дает
на фазовой плоскости (x и y) кривую
(рис.3,б), которая за один оборот не
возвращается в прежнюю точку
![]() ,
а подходит ближе к началу координат.
,
а подходит ближе к началу координат.
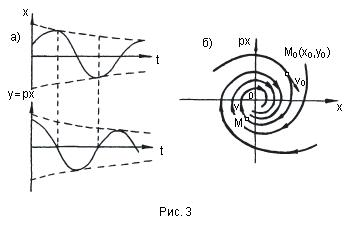
Итак, затухающим колебаниям системы (рис. 3,а) отвечают фазовые траектории в виде спиралей, по которым изображающая точка приближается к началу координат (рис. 3,б).
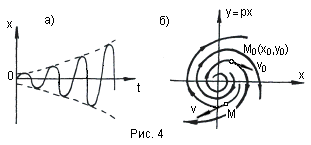
С л у ч а й 3. Этот случай (комплексные корни с положительными вещественными частями) соответствует расходящимся колебаниям (рис.4,а). Рассуждая аналогично предыдущему, получим всю совокупность возможных фазовых траекторий тоже в виде спиралей, но только изображающая точка будет двигаться по ним не к началу координат, а от него (рис.4,б).
С л у ч а й 4. Этот случай (вещественные отрицательные корни) соответствует апериодическому процессу
![]() ,
,
![]() ,
(1.6)
,
(1.6)
где
![]()
На рис.6,а показаны
два возможных варианта (кривые 1
и 2) протекания
такого процесса. Легко видеть, что на
фазовой плоскости (x,
y)
это изобразится кривыми 1
и 2 соответственно
(рис. 6,б), так как в первом варианте все
время x>0
и y<0,
а во втором варианте знаки x
и y
меняются по одному разу. Границы областей
1 и 2 представляют
собой прямые y
= -![]() x
и y
= -
x
и y
= -![]() x
получающиеся из уравнений (1,6),
соответственно при
x
получающиеся из уравнений (1,6),
соответственно при
![]() =
0 и при
=
0 и при
![]() =
0
(обращение одного из корней в нуль).
=
0
(обращение одного из корней в нуль).
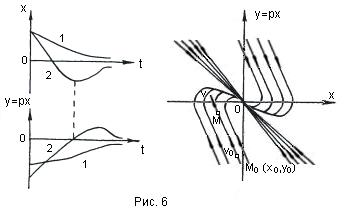
В отличие от прежнего здесь все фазовые траектории вливаются непосредственно в начало координат О фазовой плоскости. Однако изображающая точка М не попадает в начало координат в конечное время, а приближается асимптотически.
Итак, затухающим апериодическим процессам в системе отвечают фазовые траектории, вливающиеся в начало координат.
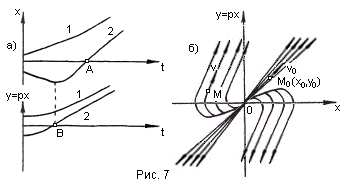
С л у
ч а й 5. Этот случай (вещественные
положительные корни) соответствует
также апериодическому процессу,
определяемому теми же уравнениями
(1.6), но при
![]() <0
и
<0
и
![]() <0.
Аналогично предыдущему получаем кривые
процесса и фазовые траектории, изображенные
на рис.7.
<0.
Аналогично предыдущему получаем кривые
процесса и фазовые траектории, изображенные
на рис.7.
С л у
ч а й 6. В этом случае (вещественные корни
разных знаков) также имеет место
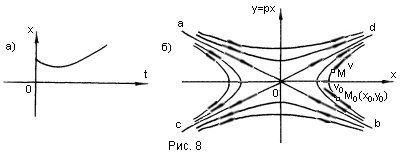
апериодический процесс (1.6) (рис.8,а), где
![]() и
и
![]() имеют
разные знаки, на картина фазовых
траекторий здесь иная. Так как
имеют
разные знаки, на картина фазовых
траекторий здесь иная. Так как
![]() <0,
то введем обозначение
<0,
то введем обозначение
![]() =
=
![]() ,
причем для простоты построений рассмотрим
случай
,
причем для простоты построений рассмотрим
случай
![]() =
= 0, что
соответствует согласно (1.2) уравнению
системы
=
= 0, что
соответствует согласно (1.2) уравнению
системы
![]() и согласно (1.4) – уравнению фазовых
траекторий
и согласно (1.4) – уравнению фазовых
траекторий
![]() (1.7)
(1.7)
Интегрирование
последних, аналогично случаю 1, дает
![]() ,
т.е. семейство гипербол, изображенное
на рис. 8 б.
,
т.е. семейство гипербол, изображенное
на рис. 8 б.
Направления движения изображающей точки М по фазовым траекториям, показанные на рис. 8,б, легко определяются в каждой четверти плоскости по знаку dy/dx (1.7).
Аналогичная
картина фазовых траекторий получится
в данном случае и при
![]() .
.
Итак, расходящимся апериодическим процессам в системе отвечают фазовые траектории типа рис.7, б или 8,б, причем изображающая точка, двигаясь по ним, в конечном итоге удаляется от начала координат.