
Оценка остатка ряда с положительными членами
|
Пусть дан ряд
Утверждение об оценке остатка ряда.Если для ряда с положительными членами
существует такое число Действительно,
условие
|
Для выполнения следующего упражнения, Вам, возможно, понадобится оператор цикла с неопределенным числом операций while … end. Его синтаксис:
while<логическое выражение>
<инструкции>
еnd
Этот оператор многократно выполняет инструкцию или группу инструкций, пока логическое выражение истинно. Логическое выражение имеет форму:
выражение <оператор отношения> выражение
оператор отношения: ==, <=, >=, <, >, ~
Упражнение 6.Пусть к ряду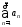 применимо утверждение об оценке ряда.
СоздайтеM-функцию, которая
оценивает число членов, достаточное
для вычисления суммы ряда с заданной
точностью
применимо утверждение об оценке ряда.
СоздайтеM-функцию, которая
оценивает число членов, достаточное
для вычисления суммы ряда с заданной
точностью ,
и вычисляет сумму ряда с заданной
точностью. В качестве входных параметровM-функции используйте
формулу общего члена последовательности
и точность
,
и вычисляет сумму ряда с заданной
точностью. В качестве входных параметровM-функции используйте
формулу общего члена последовательности
и точность .
Применить созданную М-функцию для
вычисления с точностью до 0,001 суммы
ряда:
.
Применить созданную М-функцию для
вычисления с точностью до 0,001 суммы
ряда:
а)
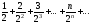 б)
б)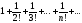
Указание. Для ряда
а) имеем: - при увеличении
- при увеличении монотонно уменьшается от
монотонно уменьшается от до
до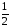 .
Для ряда б):
.
Для ряда б):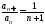 - убывает от
- убывает от до нуля. Наша М-функция может содержать
два цикла. В первом цикле, начиная с
до нуля. Наша М-функция может содержать
два цикла. В первом цикле, начиная с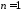 ,
вычисляем
,
вычисляем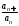 и
и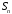 до тех пор пока выполняется неравенство
до тех пор пока выполняется неравенство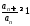 .
Во втором цикле продолжаем вычислять
.
Во втором цикле продолжаем вычислять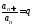 и
и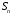 ,
а также
,
а также .
Второй цикл заканчивается при выполнении
условия
.
Второй цикл заканчивается при выполнении
условия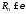 .
Выходными параметрами М-функции должны
быть
.
Выходными параметрами М-функции должны
быть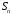 и
и .
.
Знакочередующиеся ряды
|
Назовем ряд
Признак Лейбница.Если 1) ряд сходится; 2) для любого
остатка
|
Упражнение 7.СоздатьM-функцию,
которая оценивает число членов
знакочередующихся рядов, достаточное
для вычисления суммы ряда с заданной
точностью ,
и вычисляет сумму ряда с заданной
точностью. В качестве входных параметровM-функции использовать
формулу общего члена последовательности
и точность
,
и вычисляет сумму ряда с заданной
точностью. В качестве входных параметровM-функции использовать
формулу общего члена последовательности
и точность .
.
Для следующих рядов доказать сходимость и применить созданную М-функцию для вычисления с точностью до 0,001 суммы ряда:
а)
 б)
б) .
.

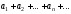 .
Назовем ряд
.
Назовем ряд ,
полученный из исходного отбрасыванием
первых
,
полученный из исходного отбрасыванием
первых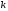 членов ряда,
членов ряда,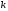 -м
остатком ряда. Если сходится ряд
-м
остатком ряда. Если сходится ряд ,
то сходится и его остаток, причем их
суммы связаны соотношением
,
то сходится и его остаток, причем их
суммы связаны соотношением (здесь
(здесь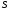 - сумма ряда,
- сумма ряда,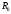 - сумма остатка).
- сумма остатка). ,
что при всех
,
что при всех ,
начиная с некоторого
,
начиная с некоторого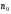 ,
выполняется неравенство
,
выполняется неравенство ,
то сумма
,
то сумма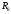
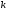 -го
остатка при
-го
остатка при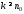 удовлетворяет неравенству
удовлетворяет неравенству .
.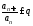 ,
выполняемое для всех номеров больших
,
выполняемое для всех номеров больших ,
означает, что члены ряда, начиная с
,
означает, что члены ряда, начиная с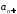 ,
стремятся к нулю не медленней членов
геометрической прогрессии с данным
,
стремятся к нулю не медленней членов
геометрической прогрессии с данным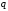 ,
а значит и остаток ряда будет не больше
суммы бесконечной геометрической
прогрессии, т.е.
,
а значит и остаток ряда будет не больше
суммы бесконечной геометрической
прогрессии, т.е.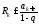 .
.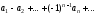 ,
где все
,
где все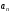 положительны,знакочередующимся.
положительны,знакочередующимся.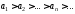 и
и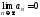 ,
то:
,
то: выполняется неравенство
выполняется неравенство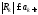 ,
причем знак
,
причем знак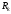 совпадает со знаком
совпадает со знаком .
.