
Необходимый признак сходимости.
В приложениях обычно применяются сходящиеся ряды. Поэтому важно знать признаки, по которым можно было бы судить, сходится данный ряд или нет.
Попробуйте установить связь между поведением общего члена ряда на бесконечности и сходимостью ряда, опираясь на результаты выполнения упр. 1.
Подтверждают или опровергают ряды, рассмотренные в упр. 1, следующие гипотезы:
а) Если ряд сходится, то последовательность
его членов стремится к нулю при
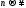 .
.
б) Если последовательность членов ряда
стремится к нулю при
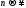 ,
то ряд сходится?
,
то ряд сходится?
Подтверждение Ваших предположений найдете на следующей странице.
|
Необходимый признак сходимости.Если ряд сходится, то его
Действительно, пусть ряд сходится,
т.е. последовательность его конечных
сумм
С учетом
равенства
|
Подчеркнем, что мы установили лишь необходимый признак сходимости, т.е. такой,при нарушении которого ряд не может сходиться. С помощью этого признака можно доказывать лишь расходимость ряда.
Упражнение 2.Расходимость каких из следующих рядов можно доказать, используя необходимый признак сходимости? Обязательно провести доказательство «вручную» и, при желании, используяMATLAB:
А )
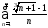 ;
б)
;
б)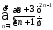 .
.
Упражнение 3. Приведите два примерарасходящихсячисловых рядов (отличные от рассмотренных в упр. 3), общий член которых стремится к нулю. ИспользуяM-функцию из упр. 1, проиллюстрируйте примеры графически.
Сделав упр. 3, Вы проиллюстрировали, что стремления общего члена ряда к нулю недостаточно для сходимости ряда.
Общие свойства рядов.
|
1) Если ряд
2) Если ряды
3) Если ряд
|
Практически в каждом учебнике по математическому анализу можно найти доказательства этих свойств (впрочем, Вы можете доказать их и самостоятельно, опираясь на свойства числовых рядов).
А что получится, если складывать расходящиеся ряды?
Упражнение 4.
а) Пусть ряд
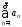 сходится,
сходится,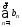 расходится. Что можно сказать о сходимости
ряда
расходится. Что можно сказать о сходимости
ряда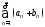 ?
Проиллюстрируйте Ваше предположение
на примере, используя М-файл из упр. 1.
?
Проиллюстрируйте Ваше предположение
на примере, используя М-файл из упр. 1.
б) Пусть ряды
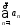 и
и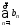 расходятся. Что можно сказать о сходимости
ряда
расходятся. Что можно сказать о сходимости
ряда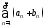 ?
Проиллюстрируйте Ваши предположения
на примерах, используя М-файл из упр. 1.
?
Проиллюстрируйте Ваши предположения
на примерах, используя М-файл из упр. 1.
Признаки сходимости рядов с положительными членами
Рассмотрим некоторые признаки сходимости числовых рядов.
|
Признак
сравнения.Пусть даны два ряда 1) если ряд (2) («больший») сходится, то и ряд (1) («меньший») сходится; 2) если ряд (1) («меньший») расходится, то и ряд (2) («больший») расходится. |
Например, рассмотрим ряд
 ,
полученный из ряда
,
полученный из ряда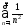 (упр. 1, п. 5) отбрасыванием первых двух
членов. Его можно сравнить с рядом
(упр. 1, п. 5) отбрасыванием первых двух
членов. Его можно сравнить с рядом ,
сходимость которого ранее доказана
(упр. 1, п.6). Так как
,
сходимость которого ранее доказана
(упр. 1, п.6). Так как и «больший» ряд сходится, то сходится
и «меньший» ряд
и «больший» ряд сходится, то сходится
и «меньший» ряд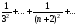 ,
а, значит, и ряд
,
а, значит, и ряд .
.
|
Предельный признак сравнения. Пусть даны
два ряда
1) если одни из рядов сходится, то сходится и другой; 2) если одни из рядов расходится, то расходится и другой. |
Докажем, что расходится (гармонический)
ряд (упр. 1 п. 4). Используем для сравнения ряд
(упр. 1 п. 4). Используем для сравнения ряд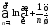 .
Заметим, что
.
Заметим, что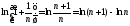 и найдем частичные суммы ряда
и найдем частичные суммы ряда :
: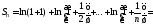
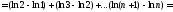
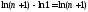 .
Отсюда следует, что
.
Отсюда следует, что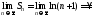 ,
т.е. ряд
,
т.е. ряд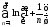 расходится. Но
расходится. Но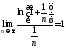 ,
значит, из расходимости ряда
,
значит, из расходимости ряда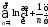 следует расходимость ряда
следует расходимость ряда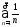 .
.
|
Признак
Даламбера.Если для ряда существует предел
|
Рассмотрим ряд
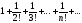 .
.
Имеем
 ,
следователь, ряд сходится.
,
следователь, ряд сходится.
|
Интегральный признак Коши. Пусть функция
|
Выясним, при каких
 сходится ряд
сходится ряд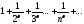 .
Положим
.
Положим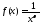 (
(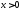 ).
Функция
).
Функция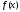 положительна, монотонно убывает. Поэтому
ряд
положительна, монотонно убывает. Поэтому
ряд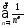 сходится тогда и только тогда, когда
сходится интеграл
сходится тогда и только тогда, когда
сходится интеграл .
Этот интеграл сходится при
.
Этот интеграл сходится при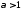 и расходится при
и расходится при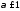 .
Значит, и ряд
.
Значит, и ряд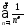 сходится при
сходится при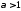 и расходится при
и расходится при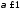 .
.
Упражнение 5.Опираясь на признаки сходимости, доказать:
а) ряд
 расходится; б) ряд
расходится; б) ряд сходится;
сходится;
в) ряд
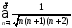 сходится; г) ряд
сходится; г) ряд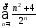 сходится;
сходится;
д) ряд
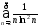 сходится; е)
сходится; е) расходится.
расходится.
(сделать дома и принести как часть отчета по лабораторной работе).

 -й
член стремится к нулю при
-й
член стремится к нулю при .
. имеет конечный предел при
имеет конечный предел при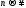 .
Тогда для этой последовательности
выполняется условие Коши:
.
Тогда для этой последовательности
выполняется условие Коши: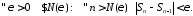
 ,
последнее выражение является
определением того, что последовательность
,
последнее выражение является
определением того, что последовательность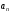 стремится к нулю при
стремится к нулю при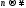 .
.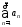 сходится, то сходится и любой ряд,
полученный из него отбрасыванием
конечного числа членов.
сходится, то сходится и любой ряд,
полученный из него отбрасыванием
конечного числа членов.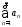 и
и сходятся, а их суммы соответственно
равны
сходятся, а их суммы соответственно
равны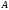 и
и ,
то сходится и ряд
,
то сходится и ряд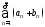 ,
причем его сумма равна
,
причем его сумма равна .
.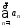 сходится и его сумма равна
сходится и его сумма равна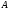 ,
то сходится и ряд
,
то сходится и ряд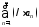 ,
причем его сумма равна
,
причем его сумма равна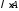 .
. (1) и
(1) и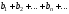 (2) , с положительными членами, причем
(2) , с положительными членами, причем .
Тогда
.
Тогда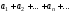 и
и с положительными членами,
с положительными членами,
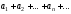 с положительными членами
с положительными членами ,
то ряд сходится в случае
,
то ряд сходится в случае и расходится в случае
и расходится в случае .
.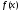 определена для
определена для ,
положительна, монотонно убывает и для
всех
,
положительна, монотонно убывает и для
всех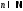 имеет место равенство
имеет место равенство .
Тогда для сходимости числового ряда
.
Тогда для сходимости числового ряда необходимо и достаточно, чтобы сходился
несобственный интеграл
необходимо и достаточно, чтобы сходился
несобственный интеграл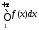 (иными словами ряд
(иными словами ряд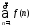 сходится или расходится одновременно
с
сходится или расходится одновременно
с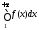 ).
).