
Лабораторная работа № 3 «Числовые ряды» (практикумы 3 и 4).
|
Числовой ряд. Частичные суммы ряда. Сходящиеся и расходящиеся ряды. Сумма ряда. Общие свойства рядов. Необходимый признак сходимости. Признаки сравнения рядов. Оценка остатка ряда. |
|
Структура цикла с неопределенным числом повторений WHILE … END. |
Числовой ряд. Сходящиеся и расходящиеся ряды. Сумма ряда.
|
Пусть задана бесконечная последовательность
чисел
Член ряда
|
Например,
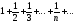 есть ряд с общим членом
есть ряд с общим членом ,
а
,
а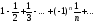 есть ряд с общим членом
есть ряд с общим членом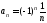 .
.
|
Числа
и т.д. называются
частичными суммамиряда. Обобщая:
|
В качестве примера рассмотрим ряд
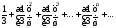 ..
Члены этого ряда
..
Члены этого ряда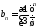 ,
,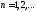 ,
образуют геометрическую прогрессию с
первым членом
,
образуют геометрическую прогрессию с
первым членом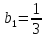 и знаменателем
и знаменателем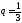 и, значит,
и, значит, -я
частичная сумма
-я
частичная сумма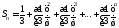 этого ряда является суммой первых
этого ряда является суммой первых членов геометрической прогрессии и
может быть найдена по формуле
членов геометрической прогрессии и
может быть найдена по формуле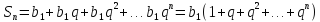 ,
,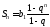 .
Таким образом,
.
Таким образом,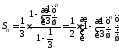 .
.
|
Если последовательность
Если же
|
Продолжим рассмотрение примера. Для
ряда
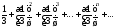 конечный предел частичных сумм существует:
конечный предел частичных сумм существует: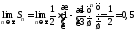 .
Следовательно, этот ряд сходится и его
сумма равна
.
Следовательно, этот ряд сходится и его
сумма равна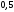 .
.
Все упражнения аккуратно проделать и сделать дома в тонких тетрадях, и принести как часть отчета по лабораторной работе
Упражнение 1. СоздатьM-функцию,
которая строит в одной системе координат
график последовательности членов ряда
и график последовательности частичных
сумм ряда. При построении этой пары
графиков использовать разные цвета и
маркеры. В качестве входных параметровM-функции использовать
формулу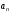 общего члена последовательности и число
общего члена последовательности и число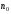 рассматриваемых членов. В качестве
выходных параметров вывести значения
рассматриваемых членов. В качестве
выходных параметров вывести значения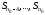 .
Применить созданную М-функцию для
исследования следующих рядов:
.
Применить созданную М-функцию для
исследования следующих рядов:
1)
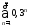 ;
2)
;
2)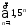 ;
3)
;
3)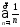 ;
4)
;
4)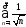 ;
5)
;
5)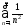 ;
6)
;
6)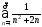 .
.
а) Опираясь на построенные графики, для каждого ряда выдвинуть гипотезу о сходимости или расходимости ряда. В случае предположения о сходимости ряда указать приблизительное значение суммы ряда.
б) Для 1, 2 и 6 рядов доказать, опираясь
на определение, выдвинутую гипотезу о
сходимости (расходимости) ряда, и в
случае сходимости ряда, найти точное
значение суммы (сделать дома и принести
как часть отчета по лабораторной работе;
указание для 6-го ряда: общий член ряда
разложить на сумму элементарных дробей
и получить выражение для
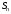 ).
).
Рекомендации к упр.1:
Как вариант, можно построить графики в
одном графическом окне, но в разных
графических областях, т.е. воспользоватьсяsubplot. В одной графической области
построить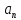 ,в
другой
,в
другой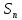 .
.
В любом случае
для наглядности получаемых результатов
рекомендую включить паузу после каждого
действия
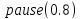 ,
,
А для
автоматизации создания хорошей системы
координат не писать
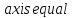 ,
но написать
,
но написать
axis([-1 N+1 -1 max(a_n)+1]),
line([-1 0; N+1 0],[0 -1;0 max(S)+1],'LineWidth',1,'Color','black')

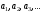 Рассмотрим выражение
Рассмотрим выражение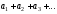 ,
представляющее собой «сумму бесконечного
множества слагаемых». Оно называетсячисловым рядом, а сами числа
,
представляющее собой «сумму бесконечного
множества слагаемых». Оно называетсячисловым рядом, а сами числа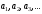 -членами ряда.
-членами ряда.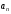 с произвольным номером
с произвольным номером называетсяобщим членом.
называетсяобщим членом.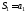 ,
,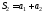 ,
,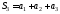
 -я
частичная сумма
-я
частичная сумма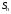 есть сумма первых
есть сумма первых членов ряда:
членов ряда: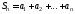 .
.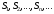 частичных сумм ряда имеет конечный
предел, т.е. существует число
частичных сумм ряда имеет конечный
предел, т.е. существует число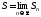 ,
то ряд называется сходящимся, а число
,
то ряд называется сходящимся, а число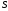 называется суммой ряда. В этом случае
также говорят, чторяд сходится к
сумме
называется суммой ряда. В этом случае
также говорят, чторяд сходится к
сумме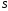 и пишут
и пишут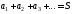 .
.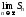 равен бесконечности или не существует,
то говорят, что рядрасходитсяили, что он не имеет суммы.
равен бесконечности или не существует,
то говорят, что рядрасходитсяили, что он не имеет суммы.