19.Уметь получать законы распределения отдельных компонент по таблице распределения двумерной дискретной св

Y X	–1	1	Pi
0	0,1	0,06	0,16
1	0,3	0,18	0,48
2	0,2	0,16	0,36
Pj	0,6	0,4	1

Найти одномерные законы распределения компонент X и Y.

Найти вероятность того, что – ?

– ?

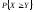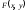Решение.

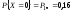
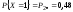
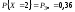
X	0	1	2
P	0,16	0,48	0,36

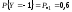
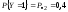
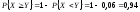
Y X	y  –1	–1 < y  1	y > 1
x  0	0	0	0
0 < x  1	0	0,1	0,16
1 < x  2	0	0,4	0,64
x > 2	0	0,6	1

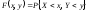
20.Определение двумерной плотности распределения и ее основные свойства.

Двумерной плотностью распределения 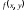называется такая функция, что вероятность 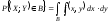, где .

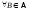Свойства.

I. .

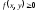II. 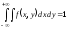(условие нормировки).

III. .

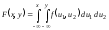IV. .

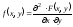21.Понятие независимости СВ, необходимые и достаточные условия независимость СВ.

Две СВ X и Y называются независимыми, если независимы все связанные с ними события

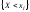
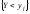
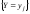
В терминах законов распределения, независимость СВ можно определить так: две СВ называются независимыми, если закон распределения каждой из них не зависит от того какое значение приняла другая.

Если компоненты X и Y двумерного вектора (X, Y) независимы, то функция распределения 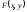выражается, через функции распределения отдельных компонент.

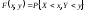
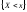и – независимы.

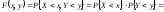
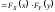
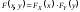
Это правило является необходимым и достаточным условием независимости для любого типа СВ.

22.Уметь вычислять основные числовые характеристики двумерных дискретных СВ: мат.ожидание и дисперсии компонент, ковариацию и коэффициент корреляции.

Пример.

Y X	0	2	5	Pi
1	0,1	0	0,2	0,3
2	0	0,3	0	0,3
4	0,1	0,3	0	0,4
Pj	0,2	0,6	0,2	

Найти: – ?

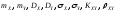Решение.

Очевидно, что компоненты X и Y зависимы.

,

,

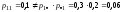
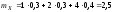
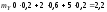
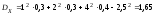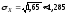
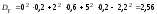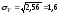
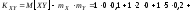
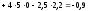
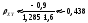
, значит между компонентами X и Y существует отрицательная линейная зависимость.

23.Знать определения: выборки, вариационного ряда, полигона, гистограммы, эмпирической функции распределения.

Совокупность чисел , полученных в результате n-кратного повторения опыта по измерению генеральной совокупности X, называется реализацией случайной выборки или просто выборкой объёма n.

Выборка  объёма n из генеральной совокупности X, упорядоченная в порядке неубывания элементов, т.е. , называется вариационным рядом:

.

Полигон частот - это ломанная, звенья которой соединяют середины горизонтальных отрезков, ограничивающих гистограмму сверху.

Гистограмма – график эмпирической плотности распределения генеральной совокупности непрерывного типа.

Для любого  обозначим через n(x) число значений выборки , удовлетворяющих неравенству . Эмпирической функцией распределения называется функция .

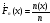24.Знать определения основных числовых характеристик выборки: выборочных среднего, дисперсии, моды и медианы.

.

.

.

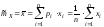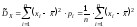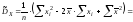
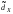– унимодального, т.е. одновершинного распределения называется элемент выборки, встречающийся с наибольшей частотой.

Выборочной медианой называется 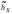, которое делит вариационный ряд на две части, содержащие равное число элементов.

Если n – нечетное число, т.е. n = 2l+1, то .

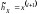Если n – четное число, т.е. n = 2l, то .

25.Знать основные требования, предъявляемые к точечным оценкам параметров генеральной совокупности, а также формулу для несмещенной оценки дисперсии.

Требования, предъявляемые к точечным оценкам:

1. Несмещенность, т.е. .

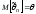Иногда оценка бывает смещенной, но асимптотически несмещенной, т.е. .

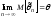2. Состоятельность, т.е. .

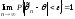3. Эффективность.

а) Если оценк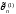и и 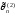– несмещенные, то 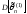и .

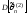Если 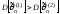, то оценка более эффективна, чем .

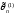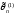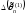б) Если оценки и – смещенные, тогда и .

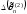Если 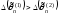, то оценка более эффективная, чем .

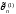Где – средний квадрат отклонения оценки.

Несмещенная оценка дисперсии:

.
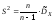
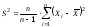