•◄ Дополнительно ►•

Пример 9–48: Заданы векторы: =(1,5,3), =(6,–4,–2), =(0,–5,7), =(–20,27,–35). Требуется подобрать числа так, чтобы образовалась замкнутая ломаная линия, составленная из векторов: , , и .

Решение:

Замечание: если рассеять туман из условия задачи, то имеется в виду что за счёт коэффициентов необходимо обеспечить: +++=0.

1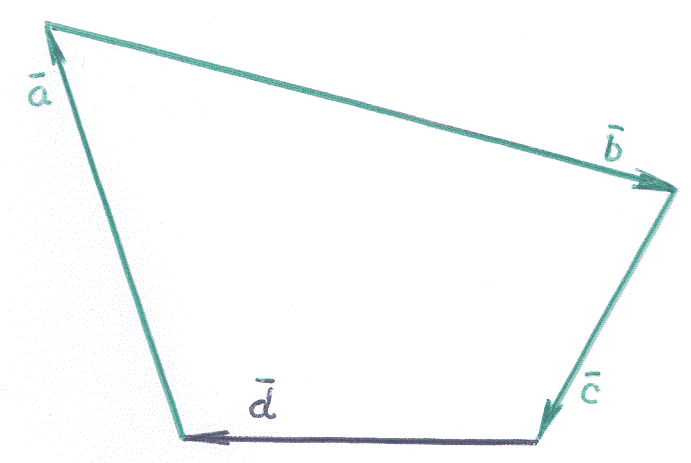). Рисунок отражает ситуацию, для которой: =1. Далее запускаем процесс:

→ , → , → .

2). Запишем равенство +++=0 в координатной форме:

3). Решая систему уравнений методом Гаусса, получаем: , , .

Ответ: числа: , , .

Пример 10–77: Зная, что =3, =1, =4 и имея равенство: ++=0 , вычислить сумму: ·+·+·.

Замечание: задачу можно отнести к этюду-шутке!

Решение:

1). Запишем сумму: . Применяя свойства ска­ляр­ного произведения, получим: .

2). Учтём: ==9, ==1, ==16. Тогда: ·+·+·=–13.

Ответ: значение суммы: ·+·+·=–13.

☻

Вопросы для самопроверки:

1. При помощи какого свойства векторов получают общее уравнение прямой?

2. Как записываются уравнения прямой линии в параметрической форме?

3. Что значит «уравнение прямой линии в отрезках»?

4. Как проводится «нормализация общего уравнения прямой линии»?

5. Что значит «угловой коэффициент» вектора, прямой?

6. Как получают уравнение прямой, проходящей через две заданные точки?

7. Что такое «отклонение» точки от заданной прямой, как его вычисляют?

8. Как определить, лежат ли заданные точки и в одной полуплоскости или в разных?

9. Как определить угол между заданными прямыми линиями?

10. Как записывают условия параллельности и перпендикулярности для двух прямых?

11. Как определить внутренний угол заданного треугольника?

Задачи для самоподготовки:

Пример C1–1: Найти длину и направляющие косинусы вектора =, если имеем =, =, =.

Ответ: длина вектора =; направляющие косинусы вектора: =, =, =.

Пример C1–2: При каких значениях величин и векторы = и = коллинеарны.

Ответ: значения: =–1, =–4.

Пример C1–3: Даны вершины треугольника : (3,–1,5), (4,2,–5), (–4,0,3). Найти длину медианы, проведённой из вершины .

Ответ: длина медианы:= 7.

Пример C1–4: Даны вершины треугольника : (1,–1,–3), (2,1,–2), (–5,2,–6). Найти длину биссектрисы его внутреннего угла при вершине .

Ответ: длина биссектрисы: =.

Пример C1–5: Треугольник задан координатами своих вершин: (3,–2,1), (3,1,5), (4,0,3). Вычислить расстояние от начала координат до точки пересечения медиан этого треугольника.

Ответ: расстояние: =.

Пример C1–6: Заданы векторы: =3, =4, угол между векторами и равен . Вычислить: а) скалярное произведение векторов =; б) ; в) .

Ответ: по пунктам: а) 9, б) –61, в) 13.

Пример C1–7: Заданы векторы: =(4,–2,–4), =(6,–3,2). Необходимо вычислить: а) ; б) ; в) направляющие косинусы вектора ; г) и , где – угол между векторами и .

Ответ: по пунктам: а) , б) , в) =, =, =, г) и =.

Пример C1–7: Найти длины сторон и величины углов треугольника с вершинами: (–1,–2,4), =(–4,–2,0), =(3,–2,1).

Ответ: стороны: =, =5, =5; углы: =, =.

< * * * * * >