
- •Московский государственный институт электронной техники (Технический Университет)
- •§2. Классическое и квантовое описание системы
- •§3. Принцип неопределенности
- •§4. Полный набор динамических переменных
- •§5. Постулаты квантовой механики
- •§6. Роль классической механики в квантовой механике
- •§7. Волновая функция и ее свойства
- •§8. Принцип суперпозиции состояний
- •§9. Понятие о теории представлений
- •§10. Операторы в квантовой механике
- •Транспонированный оператор
- •§11. Собственные функции и собственные значения эрмитовых операторов. Случай дискретного и непрерывного спектра
- •§12. Среднее значение измеряемой величины
- •§13. Вероятность результатов измерения
- •§14. Коммутативность операторов и одновременная измеримость физических величин
- •§15. Операторы координаты , импульса, момента импульса, энергии
- •§16. Решение задачи на собственные функции и собственные значения для оператора
- •§17. Решение задачи на собственные функции и собственные значения для оператора .
- •§ 18. Вычисление коммутаторов, содержащих операторы
- •§ 19 Волновое уравнение
- •§ 20 Производная оператора по времени
- •§ 21 Интегралы движения в кв. Механике
- •§22. Флуктуации физических величин
- •§ 23. Неравенство Гайзенберга
- •§ 24 Оператор Гамильтона различных систем
- •§ 25. Стационарное состояние различных систем
- •§ 26. Решение волнового уравнения в случае свободной материальной точки
- •§ 27. Решение волнового уравнения в случае бесконечно глубокой потенциальной ямы
- •§ 28. Метод (представление) Шредингера. Оператор эволюции и его свойства
- •§ 29. Метод (представление) Гайзенберга. Уравнение движения для оператора
- •§ 30. Уравнение эволюции среднего значения физической величины. Соотношение неопределенности: время – энергия
- •§ 31. Матричное представление операторов
- •§ 32. Энергетическое представление
- •§ 33. Уравнение Шредингера в матричной форме
- •§ 34*. Матричная формулировка задачи о линейном гармоническом осцилляторе
- •§ 35*. Расчет матричных элементов операторов
- •§ 36. Собственный механический момент (спин)
- •§ 37. Операторы ии их свойства
- •§ 38. Спиновая переменная волновой функции
- •§ 39. Матрицы Паули и их свойства
- •§ 40. Принцип тождественности
- •§ 41. Оператор перестановки и его свойства
- •§ 42. Симметричное и антисимметричное состояния
- •Решения задач по курсу "Квантовая теория"
- •Решения дополнительных задач по курсу "Квантовая теория"
- •Экзаменационные вопросы по курсу "Квантовая теория".
- •Экзаменационные задачи по курсу "Квантовая теория".
- •Дополнительные задачи по курсу “Квантовая теория”.
§ 36. Собственный механический момент (спин)
РассмотримNa. У него есть желтая линия . Возникает при переходе с уровня 3pна 3s.
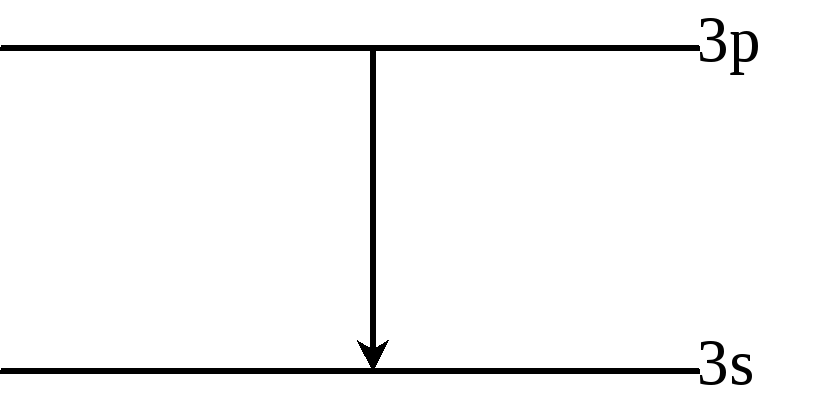
Первоначально ее длина была 5892
![]()
Было обнаружено, что эта линия расщепляется на две: дублет.
Возникла идея расщепления уровня 3pна два, тогда можно объяснить возникновение двух линий.
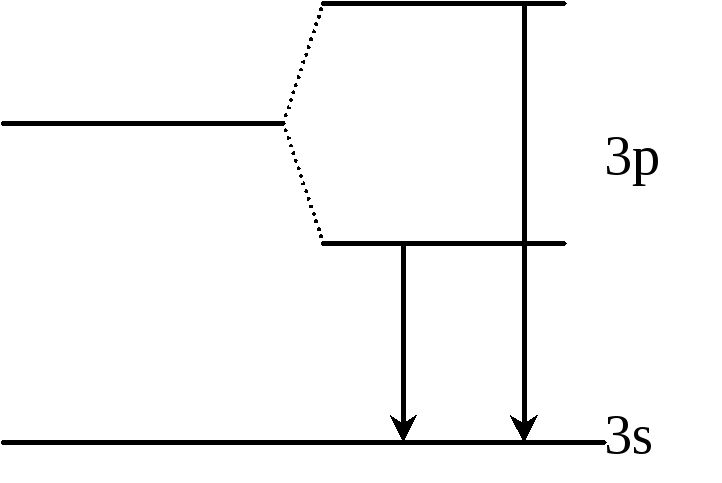
Их длины: 5896
![]() и 5890
и 5890![]() .
.
В 1925 г. Была предложена гипотеза спина, т. е. собственного механического момента.
У электрона спиновое число s=![]() .
.
Впоследствии Паули ввел спин в теорию.
Если имеем одну частицу, то она
характеризуется орбитальным квантовым
числом
![]() .
.
Составная частица (атом) состоит из
многих микрочастиц. Можно рассматривать
эту составную частицу вцелом и приписать
ей момент
![]() ,
который описывает орбитальное движение
частицы как целого.
,
который описывает орбитальное движение
частицы как целого.
Энергетический уровень этой составной
частицы в некоторых полях будет зависеть
от орбитальных моментов микрочастиц
![]() .
.
Эти моменты являются внутренним свойством этой составной частицы.
Можно рассматривать 2 момента:
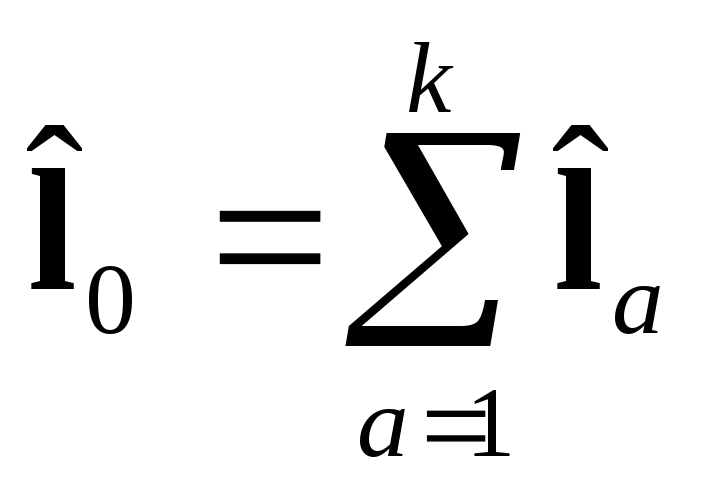 .
Этот момент описывает внутреннее
движение частицы (относительно центра
инерции)
.
Этот момент описывает внутреннее
движение частицы (относительно центра
инерции)Частица сама движется по некоторой траектории.
У частицы есть еще квантовое число
![]() ,
характеризующее собственный механический
момент.
,
характеризующее собственный механический
момент.
Вводят оператор собственного механического момента:
![]()
По аналогии
![]()
Спин – внутреннее свойство частицы. Его смысл – у частицы есть внутренний параметр, который реагирует на вращение координат независимо от места положения частицы.
§ 37. Операторы ии их свойства
Все проводится по аналогии с![]() и
и![]() .
.
![]() обладает коммутационными свойствами:
обладает коммутационными свойствами:
![]()
Так как
![]() и
и
![]() не коммутируют, то они одновременно не
измеримы.
не коммутируют, то они одновременно не
измеримы.
Но
![]() .
.
Собственные значения оператора:
![]() ,
,![]() .
.
Тогда здесь всего 2s+1 значение оператора.
Перейдем к классическому пределу:
![]()
Ввиду связи
![]() имеем
имеем![]() ,
,![]() .
.
Ясно, что так как
![]() - параметр частицы, то он не меняется ни
при каких условиях, тогда в классическом
пределе:
- параметр частицы, то он не меняется ни
при каких условиях, тогда в классическом
пределе:
![]() ,
,![]() .
.
В классической механике этим величинам аналога нет и они обращаются в нуль.
В случае спина мы не можем наложить
условие
![]() ,
т. к. спин – внутреннее свойство частицы.
Тогда
,
т. к. спин – внутреннее свойство частицы.
Тогда![]() не всегда целое число.
не всегда целое число.
Если
![]() - четное, то
- четное, то![]() -полуцелое.
-полуцелое.
Если
![]() - нечетное, то
- нечетное, то![]() -целое.
-целое.
Отсюда деление на 2 типа частиц:
Фермионы – спин полуцелый
Бозоны – спин целый.
§ 38. Спиновая переменная волновой функции
Рассмотрим одну частицу – система
с 3 степенями свободы. Задача решается
в![]() -
представлении.
-
представлении.
![]() ,
,
но есть еще внутренний параметр – спин, тогда
![]() .
.
Здесь
![]() - переменная
- переменная![]() (пространственная координата) и
(пространственная координата) и![]() (спиновая переменная, а именно проекция
спина на ось
(спиновая переменная, а именно проекция
спина на ось![]() ).
).
Здесь мы рассматриваем стационарную
задачу, поэтому
![]() отtне зависит.
отtне зависит.
Скалярное произведение теперь запишем в виде
![]()
Вероятность обнаружения частицы
![]() в объеме
в объеме![]() вблизи точки
вблизи точки![]() :
:
![]()
Если хотим найти реализацию конкретного
значения
![]() :
:
![]()
Рассмотрим действие операторов в пространстве четырех переменных
Было известно
![]() (43.1)
(43.1)
Обобщим (43.1) на случай четырех переменных:
![]() (43.2)
(43.2)
Рассмотрим случай когда
![]() действует только на спиновую переменную.
В этом случае ядро будет следующим
действует только на спиновую переменную.
В этом случае ядро будет следующим
![]()
и интеграл (43.2) переходит в интеграл:
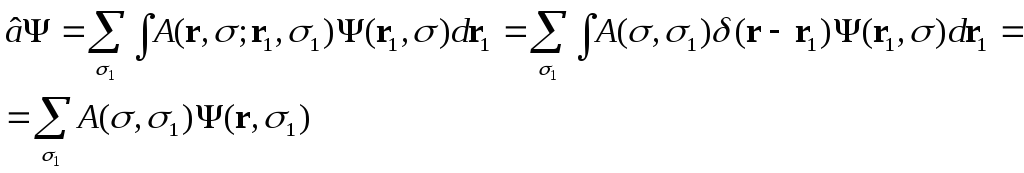
Тогда
![]()
Переменная
![]() здесь не играет большой роли. В дальнейшем
будем ее опускать, тогда
здесь не играет большой роли. В дальнейшем
будем ее опускать, тогда
![]()
Функция
![]() имеет 2s+1 переменную.
имеет 2s+1 переменную.
Ядро
![]() в дискретных переменных вырождается в
матрицу, т. е. это есть матрица размером
в дискретных переменных вырождается в
матрицу, т. е. это есть матрица размером
![]() .
.
