§ 28. Метод (представление) Шредингера. Оператор эволюции и его свойства
Существует два подхода к описанию квантово-механических систем. Согласно одному из них эволюция описывается с помощью временной зависимости волновой функции. А согласно другому – с помощью временной зависимости оператора, а волновая функция фиксирована.
В классической механике движение
системы описывается движением фазовой
точки по фазовой траектории. В классической
механике существует понятие канонического
преобразования переменных: мы можем не
говорить конкретно о динамическом
импульсе
и динамической координате
,
т. к. существует каноническое преобразование
от одних координат к другим
Движение материальной точки можно описывать с помощью канонического преобразования от координат в начальный момент времени к координатам в конечный момент времени. Т. е. эволюция классической системы может быть описана с помощью канонического преобразования.
Мы имеем уравнение Шредингера
т .
Оно позволяет найти волновую функцию, описывающую эволюцию системы.
.
Но существует и
,
где
- начальный момент времени.
Существует преобразование, которое описывает эволюцию системы:
.
(33.1)
Зная оператор
можем перейти из начального состояния
в конечное.
Подставим (33.1) в уравнение Шредингера
Отметим, что
- неявно зависит от динамических координат
Далее переносим все в одну часть и выносим волновую функцию за скобки
Более сложный случай, когда оператор
зависит от времени, т. е. внешнее поле
нестационарное. Уравнение (33.1) просто
решить не удается.
Будем рассматривать случай стационарного поля, когда
Для этого случая оператор
имеет вид:
Мы рассматриваем способ описания
Шредингера, в котором временная
зависимость заключена в
-функцию.
Эту зависимость можно перенести на
оператор эволюции
и свести нахождение
-функции
на нахождение оператора
.
В большинстве случаев операторы явно не зависят от времени.
.
Тогда возникает ситуация, когда
зависит от времени. Тогда вся информация
об эволюции заключена в
функции
или в операторе эволюции.
Свойства оператора эволюции:
Он удовлетворяет уравнению
,
при
,
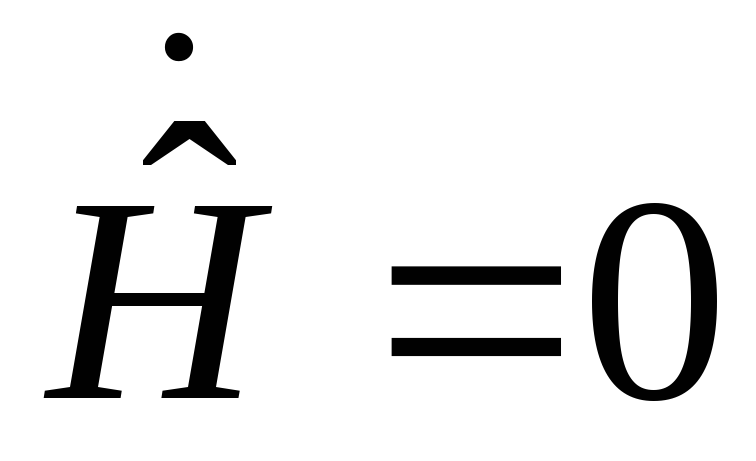- унитарный оператор.
Докажем это
Уравнение
обеспечивает сохранение нормы, т.е.
.
Норму можно взять в любой момент времени.
Подставим в условие нормировки уравнение
(1), причем положим
,
тогда
.
Таким образом
,
- унитарный оператор.
§ 29. Метод (представление) Гайзенберга. Уравнение движения для оператора
Существует подход Гайзенберга:
рассмотрим волновую функцию
как волновую функцию в некоторый момент
времени
,
т.е.
-функция
фиксированная во времен.
,
тогда
,
где
- функция в представлении Шредингера.
- функция в представлении Гайзенберга.
Но система меняется во времени. Тогда
изменение квантовой системы должно
быть связано с изменением оператора
.
Из унитарности следует
.
Напомним, что в теории представления было следующее. Преобразование функции
порождает следующее преобразование оператора
.
Как мы видим в представлении Гайзенберга
функция
явно от времени не зависит, но тогда от
времени зависит оператор
.
А в подходе Шредингера была явная зависимость волновой функции от времени, а оператор от времени явно не зависел.
Дифференцируем оператор
по времени
(34.1)
теперь запишем уравнение для оператора эволюции
Сопряженное уравнение
Тогда имеем
,
.
Подставляем эти уравнения в (34.1), получаем
={теперь видно, что в каждом слагаемом
есть
и
,
а их можно вынести за скобки}
={внутри квадратных скобок стоит оператор, над которым осуществляется преобразование, причем
,
}=
.
Получили уравнение движения для оператора
Представление Шредингера более физично и более распространено.
Представление Гайзенберга рассматривается только в некоторых системах.
При переходе из одного представления к другому результаты физических наблюдений не меняются. Эти представления унитарные инварианты.
Рассмотрим
.
Найдем
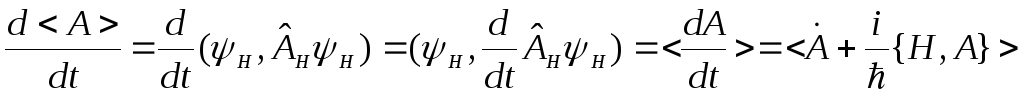
Производная от среднего есть средняя от производной.
Заметим, что под скобками <> можно писать как S, так иH, т.к. среднее инвариантно относительно преобразования.