2014

Теория вероятностей, вар 13, 2008 год.

№13. Коэффициенты использования рабочего времени у двух комбайнов соответственно равны 0,8 и 0,6. Считая, что остановки в работе каждого комбайна возникают случайно и независимо друг от друга, определить относительное время (вероятность): а) работы только одного комбайна; б) простоя обоих комбайнов.

Решение: Т.к. вероятность работы каждого комбайна в данный момент времени составляет р₁ = 0,8; р₂ = 0,6, то вероятность простоя комбайнов в этот же момент времени равна соответственно:

Учитывая, что простой и работа комбайна – случайные и независимые события, применим теоремы умножения и суммы вероятностей.

Вероятность работы только одного комбайна равна сумме вероятностей работы первого при простое второго и работы второго при простое первого:

Вероятность простоя обоих комбайнов определится произведением:

№33. Вероятность того, что пассажир опоздает к отправлению поезда, равна 0,01. Найти наиболее вероятное число опоздавших из 800 пассажиров и вероятность такого числа опоздавших.

Решение: Наивероятнейшее число появления события в независимых испытаниях, в каждом из которых вероятность появления этого события постоянна, определяется из двойного неравенства:

Из полученного неравенства, наиболее вероятно, что опоздает 8 пассажиров.

№53. На двух автоматических станках производятся одинаковые изделия, даны законы распределения числа бракованных изделий, производимых в течение смены на каждом из них для первого и для второго

Х 0 1 2 Y 0 2

р 0,1 0,6 0,3 р 0,5 0,5.

Составить закон распределения случайной величины Z = X + Y числа производимых в течение смены бракованных изделий обоими станками. Составить функцию распределения и построить её график. Проверить свойство математического ожидания суммы случайных величин.

Решение: Очевидно, число бракованных изделий есть сумма любой случайной величины Х с любой случайной величиной У.

Составим закон распределения числа бракованных изделий, как суммы любой случайной величины Х и любой случайной величины У, умножая при этом их вероятности:

Z = X + Y	0 + 0 = 0	0 + 2 = 2	1 + 0 = 1	1 + 2 = 3	2 + 0 = 2	2 + 2 = 4
Р	0,1·0,5 = 0,05	0,1·0,5 = 0,05	0,6·0,5 = 0,3	0,6·0,5 = 0,3	0,3·0,5 = 0,15	0,3·0,5 = 0,15

Объединив значения Z = 2, получим функцию распределения величины Z в табличном виде:

Z = X – У	0	1,0	2,0	3,0	4,0
Pz = Px∙Py	0,05	0,3	0,05 + 0,15 = 0,2	0,3	0,15

Составим функцию распределения:

По определению F(x) = P(X < x), поэтому:

1. При х 0; F(x) = P(X < 0) = 0;

2. При 0 < x 1; F(x) = P(X < 1) = P(X = 0) = 0,05;

3. При 0 < x 2; F(x) = P(X < 2) = 0,05 + 0,3 = 0,35;

4. При 2 < x 3; F(x) = P(X < 3) = 0,05 + 0,3 + 0,2 = 0,55;

5. При 3 < x 4; F(x) = P(X < 4) = 0,05 + 0,3 + 0,2 + 0,3 = 0,85;

6. При x >100; F(x) = P(X ≤ 4) = 0,05 + 0,3 + 0,2 + 0,3 + 0,15 = 1,000;

Т.о. функция распределения и график этой функции имеют вид:

Свойство математического ожидания – математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий.

Найдём математические ожидания величин Х и У и их сумму:

Найдём математические ожидания величины Z:

Т.о. сумма математических ожиданий случайных величин равна математическому ожиданию суммы этих величин.

№73. Случайная величина Х задана функцией распределения F(х). Найти:

1) вероятность попадания случайной величины Х в интервал (1/3; 2/3);

2) функцию плотности распределения вероятностей f(х);

3) математическое ожидание случайной величины Х;

4) построить графики F(х) и f(х).

Решение: 1. Т.к. заданный интервал (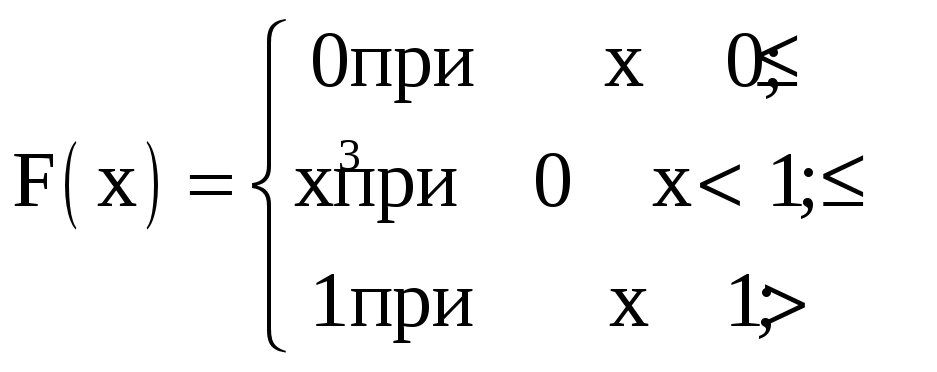1/3;2/3) входит в интервал функции

распределения 0<x<1 то, используя формулу: , получим:

2. Функция плотности вероятности есть первая производная от функции распределения:

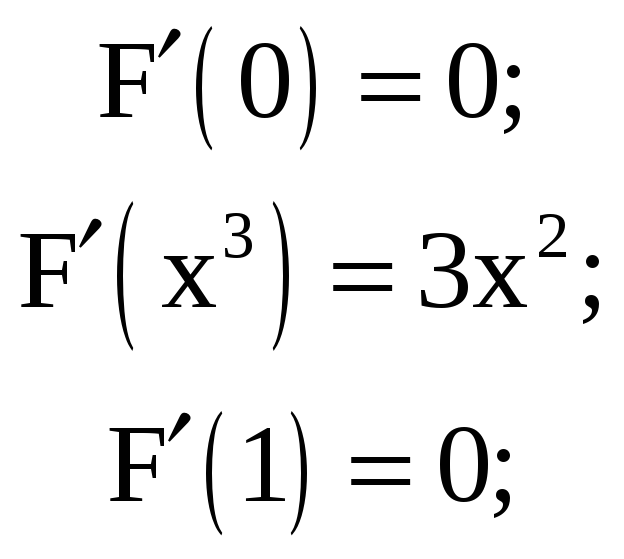Поэтому:

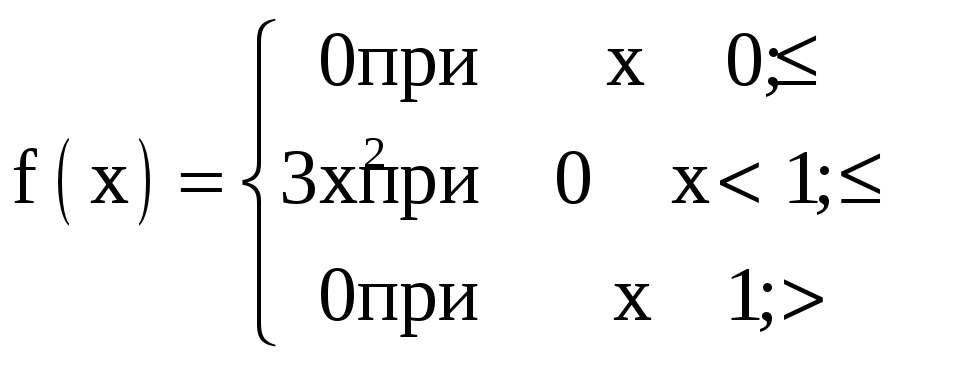
3. Математическое ожидание определится интегралом:

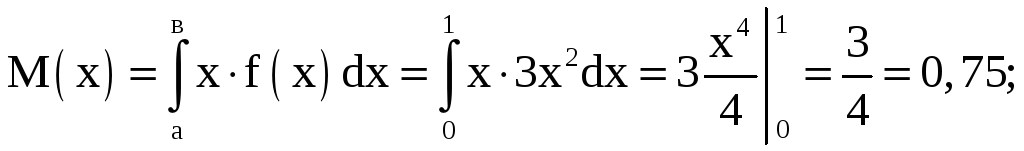
Графики F(x) и f(x) имеют вид:

№93. Текущая цена акции может быть смоделирована с помощью нормального закона распределения с математическим ожиданием "а" и средним квадратическим отклонением "σ". Требуется: а) записать функцию плотности вероятности случайной величины Х – цена акции и построить её график; б) найти вероятность того, что случайная величина Х примет значения, принадлежащие интервалу ( a, b ); в) найти вероятность того, что абсолютная величина çХ–ç окажется меньше e.

а = 26; σ = 0,7; α = 25,2; β = 26,8; ε = 0,5

Решение: а) Функция плотности вероятности для нормального распределения выражается формулой:

Г

рафик этой функции имеет максимум 0,57 при х = а = 26. Он симметричен относительно прямой f (x) = a = 26 и имеет точки перегиба, отстоящие на величину от точки а.

Т.е. при: х₁ = 26 – 0,7 = 25,3;

х₂ = 26 + 0,7 = 26,7;

Значение функции в точках перегиба соответственно равно:

f (x) = 0,57= 0,57= 0,356;

Вид графика f(x) изображён на рисунке.

б) Вероятность того, что случайная величина окажется в интервале = (25,2; 26,8), определится выражением:

где Ф(х) = 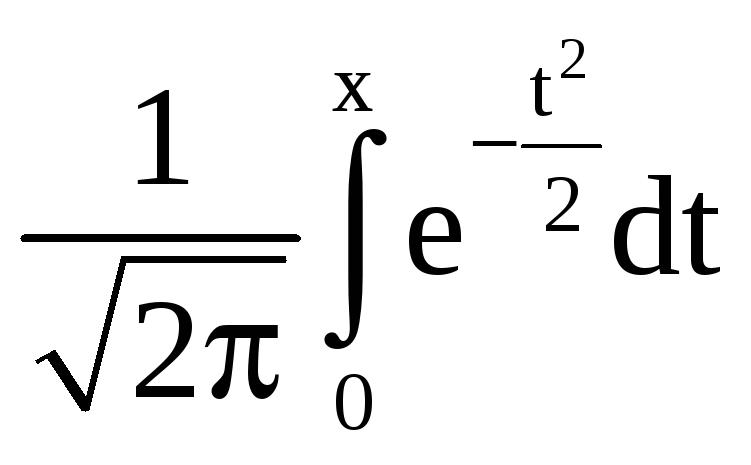– функция Лапласа.

Тогда:

в) Вероятность того, что абсолютная величина окажется меньше , определится формулой: