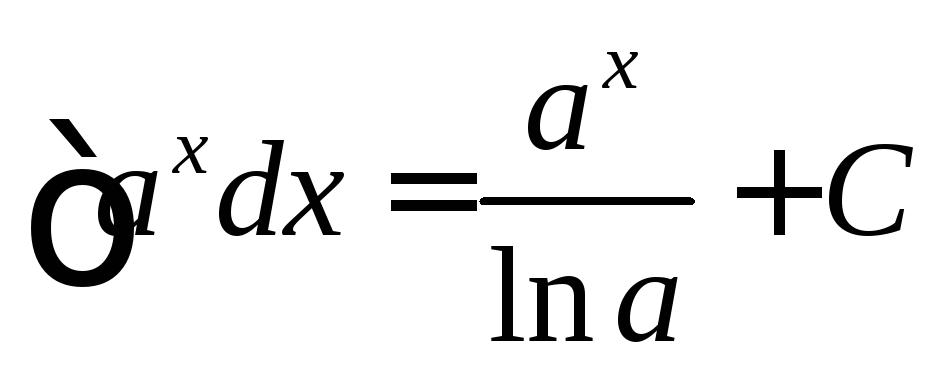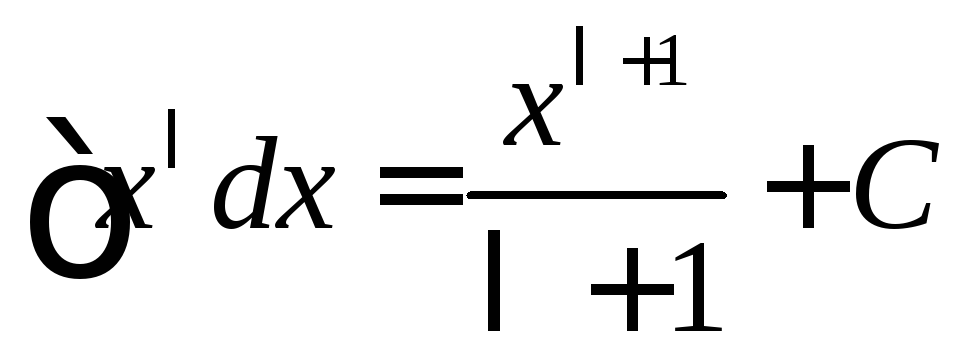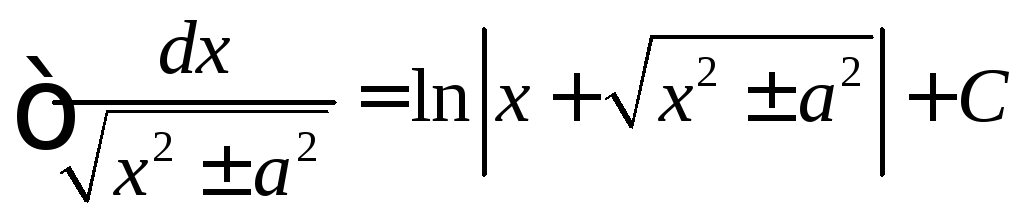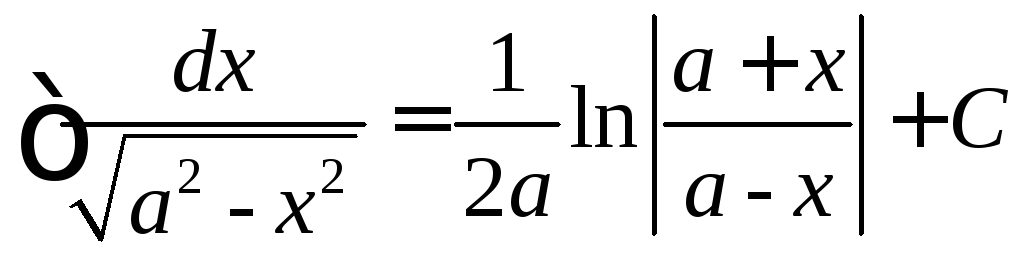Определенный интеграл функции одной переменной
Вычислить определенные интегралы.
|
№ |
Определенные интегралы |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
21 |
|
|
22 |
|
|
23 |
|
|
24 |
|
|
25 |
|
|
26 |
|
|
27 |
|
|
28 |
|
|
29 |
|
|
30 |
|
|
31 |
|
|
32 |
|
|
33 |
|
|
34 |
|
|
35 |
|
|
36 |
|
|
37 |
|
|
38 |
|
|
39 |
|
|
40 |
|
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.
Дифференциальное исчисление функции двух переменных
Задание
1.
Для функции двух переменных
,
пользуясь правилами дифференцирования,
найти производные:
.
|
№ |
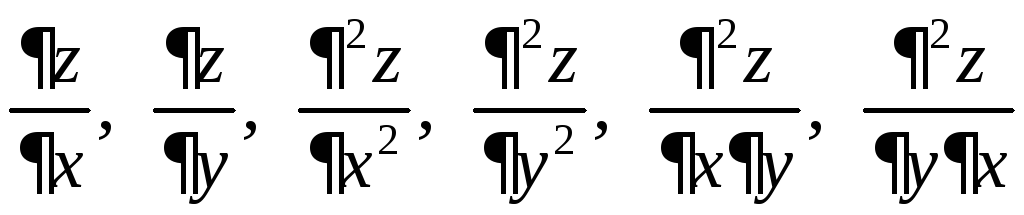Функция
|
№ |
Функция
|
|
1 |
|
2 |
|
|
3 |
|
4 |
|
|
5 |
|
6 |
|
|
7 |
|
8 |
|
|
9 |
|
10 |
|
|
11 |
|
12 |
|
|
13 |
|
14 |
|
|
15 |
|
16 |
|
|
17 |
|
18 |
|
|
19 |
|
20 |
|
|
21 |
|
22 |
|
|
23 |
|
24 |
|
|
25 |
|
26 |
|
|
27 |
|
28 |
|
|
29 |
|
30 |
|
|
31 |
|
32 |
|
|
33 |
|
34 |
|
|
35 |
|
36 |
|
|
37 |
|
38 |
|
|
39 |
|
40 |
|
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.
Задание
2.Найти
точки экстремума функции
.Характеризовать
их тип.
|
№ |
Исследуемая
функция
|
№ |
Исследуемая
функция
|
|
1 |
|
2 |
|
|
3 |
|
4 |
|
|
5 |
|
6 |
|
|
7 |
|
8 |
|
|
9 |
|
10 |
|
|
11 |
|
12 |
|
|
13 |
|
14 |
|
|
15 |
|
16 |
|
|
17 |
|
18 |
|
|
19 |
|
20 |
|
|
21 |
|
22 |
|
|
23 |
|
24 |
|
|
25 |
|
26 |
|
|
27 |
|
28 |
|
|
29 |
|
30 |
|
|
31 |
|
32 |
|
|
33 |
|
34 |
|
|
35 |
|
36 |
|
;
;
;
;
;
;
;
;
;
;
;
,
(
);
;
;
;
;
;
;
;
;
;
;
;
;
;
;
,
;
;
;
;
,
;
;
;
;
;
;МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ.
Неопределенный интеграл
Определение и основные свойства неопределенного интеграла
Функция
называется первообразной функцией для
или интегралом для
,если
производная от этой функции равна
т.е.
.
Выражение
,
где
— произвольная постоянная, представляет
собой общий вид функции, которая имеет
производную
или дифференциал
.
Это выражение называется неопределенным
интегралом и обозначается символом
в
котором неявным образом уже заключена
произвольная постоянная. Произведение
называется подынтегральным выражением,
а функция
— подынтегральной функцией.
Из определения неопределенного интеграла непосредственно вытекают следующие свойства:
1.
2.
3.
Свойство линейности
Таблица простейших интегралов
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приемы интегрирования
Замена переменных в неопределенном интеграле
Если
,
то тогда
.
(4.1)
Пусть требуется вычислить интеграл
Выбирая
в качестве новой переменной функцию
,
такую что подынтегральное выражение
представляется в виде
Цель
данного приема состоит к переходу более
удобной для интегрирования функции
.
Пример.
.
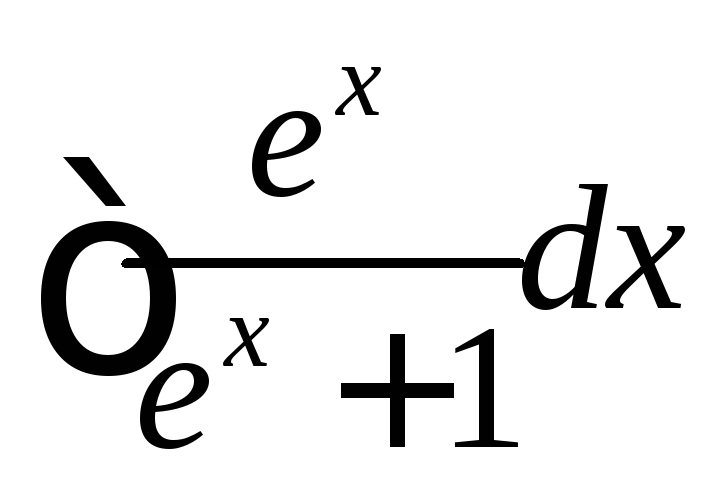Вводя
,
получаем
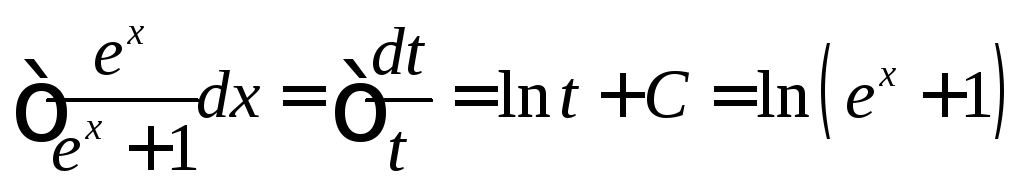
Интегрирование по частям
Этот
прием представляет сведение данного
интеграла
к интегралу
с помощью формулы
(4.2)
Этот
прием ведет к цели, если
находится легче, чем
.
Это правило хотя и имеет более ограниченную область применения по сравнению с заменой переменной, существует целый класс функций, который интегрируется именно с помощью этого метода. Сюда можно отнести:
где
есть любое целое положительное число.
Применение
формулы (4.2) предусматривает последовательное
понижение степени
до нулевой.
Интегрирование простых дробей
К простым дробям относятся
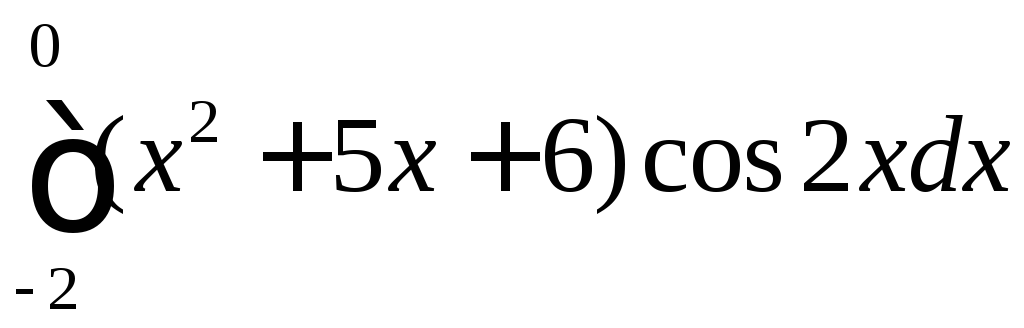
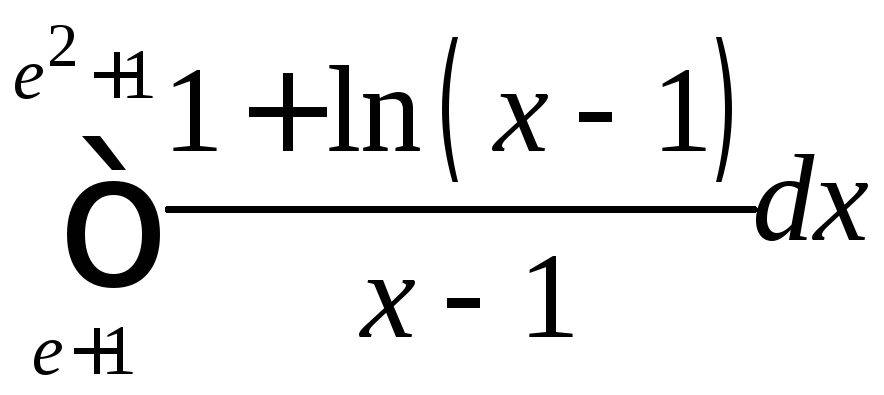
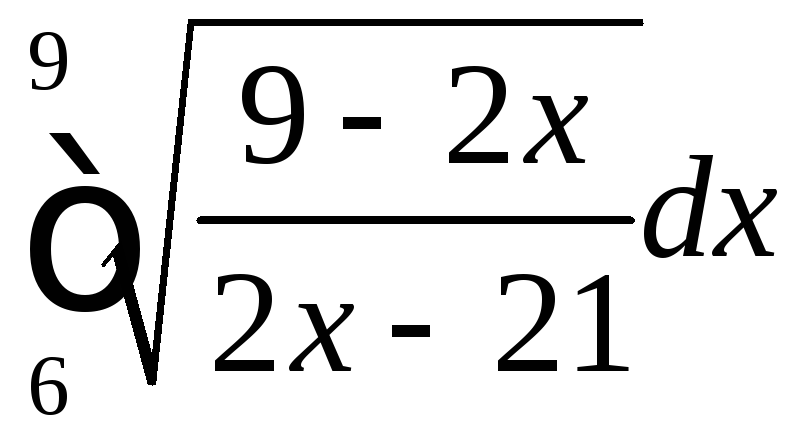
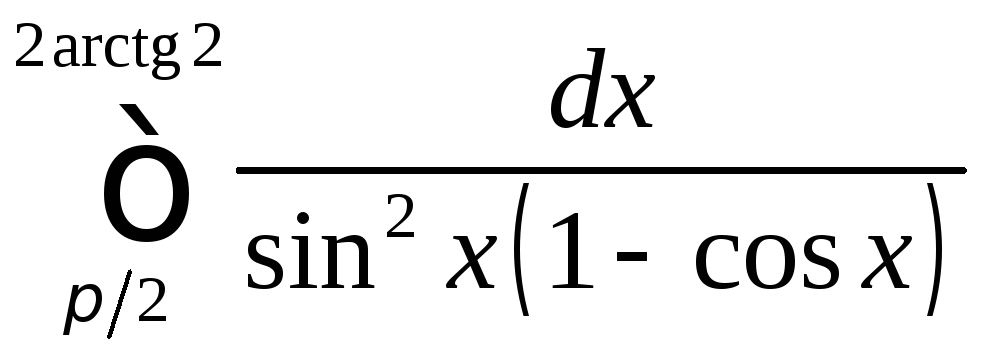
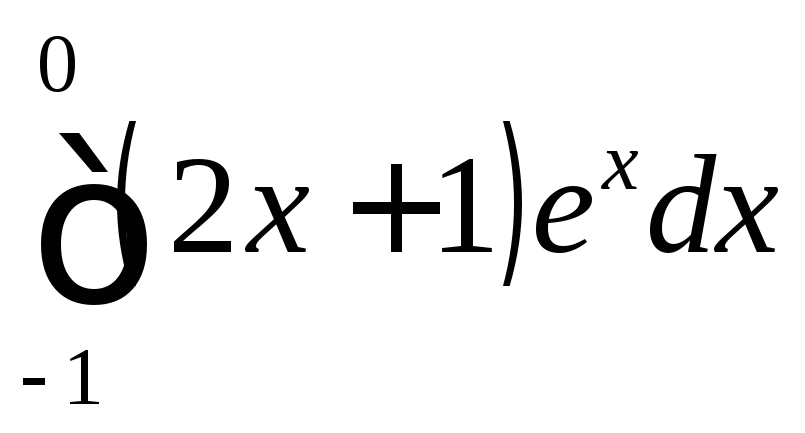
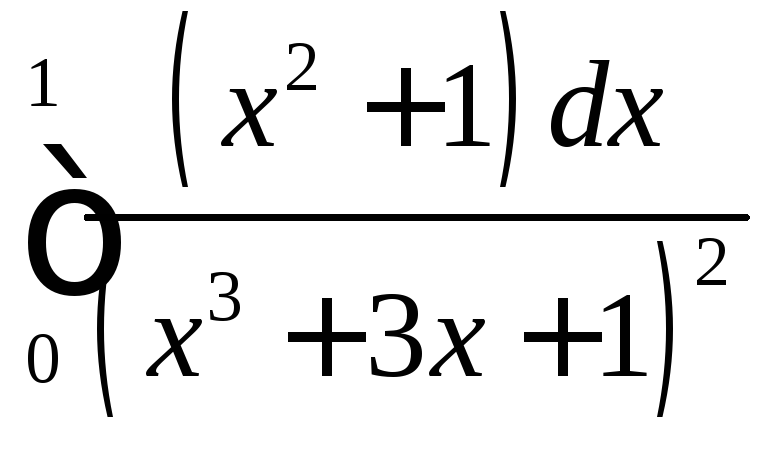
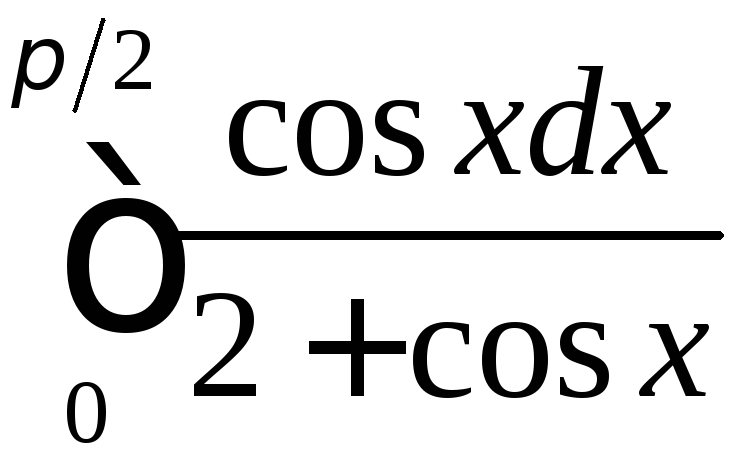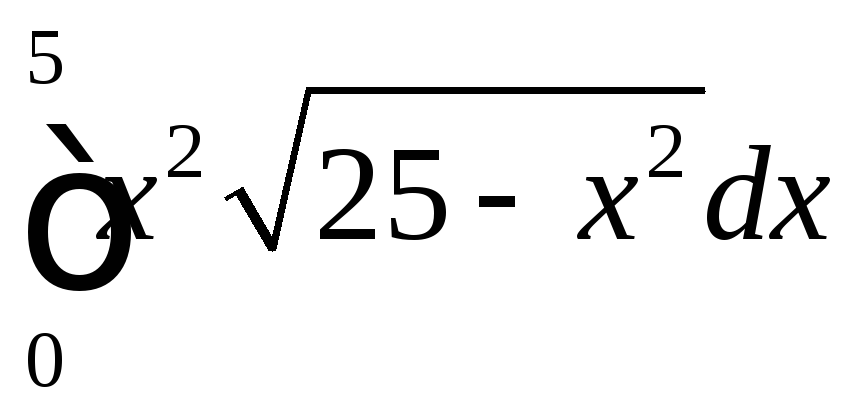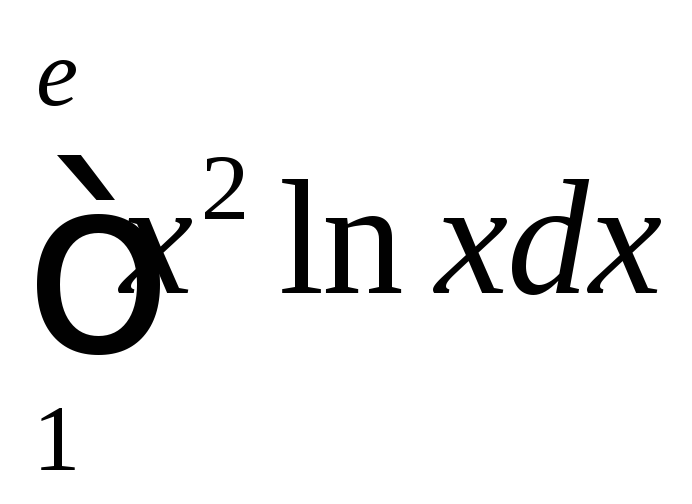
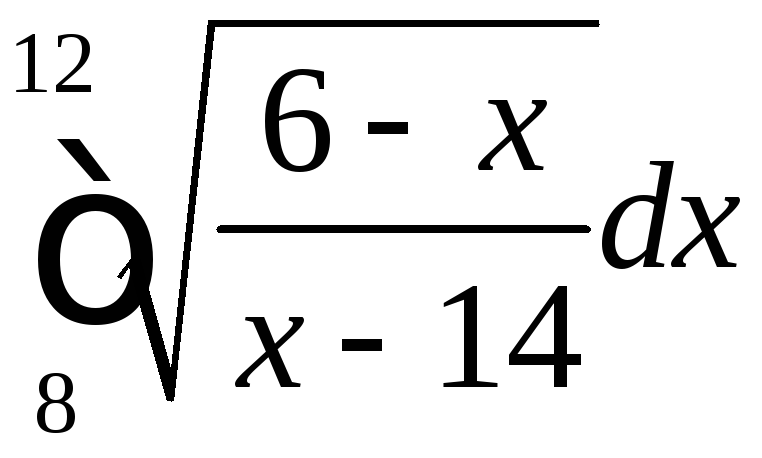
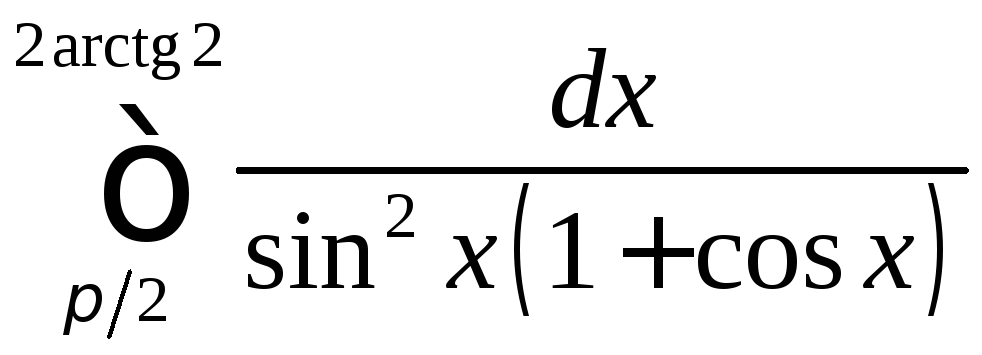
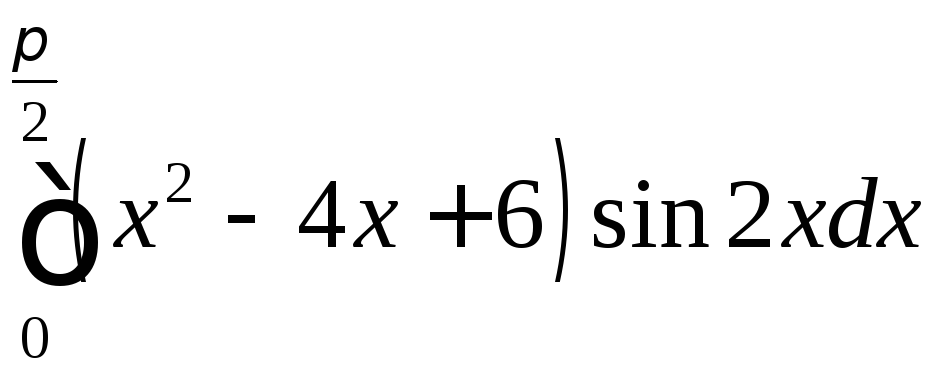
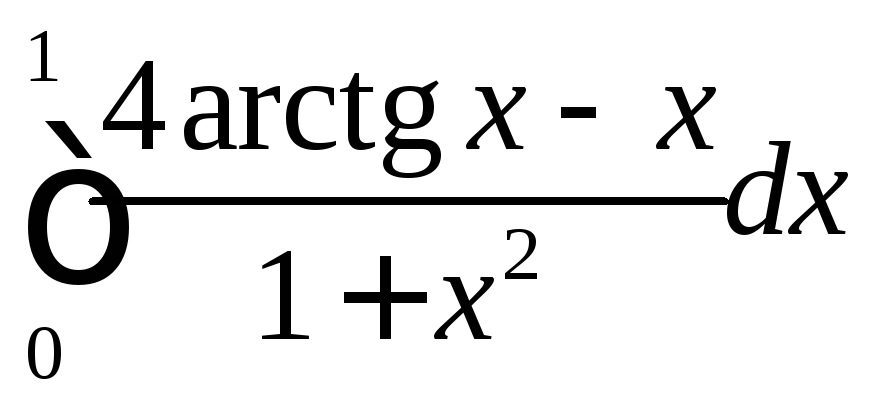
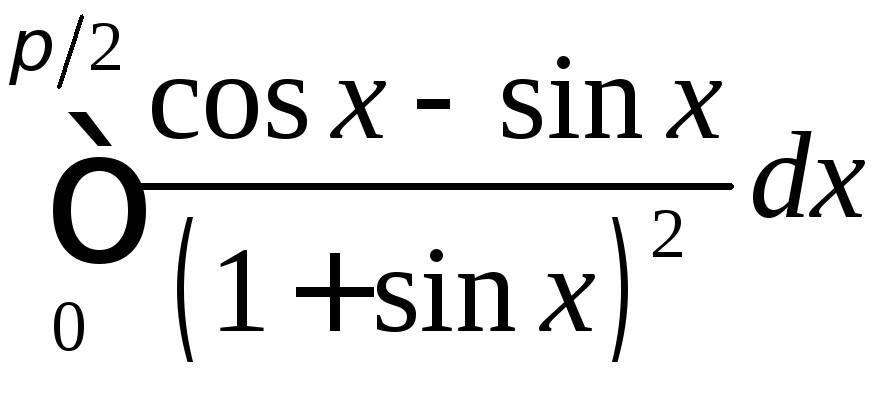
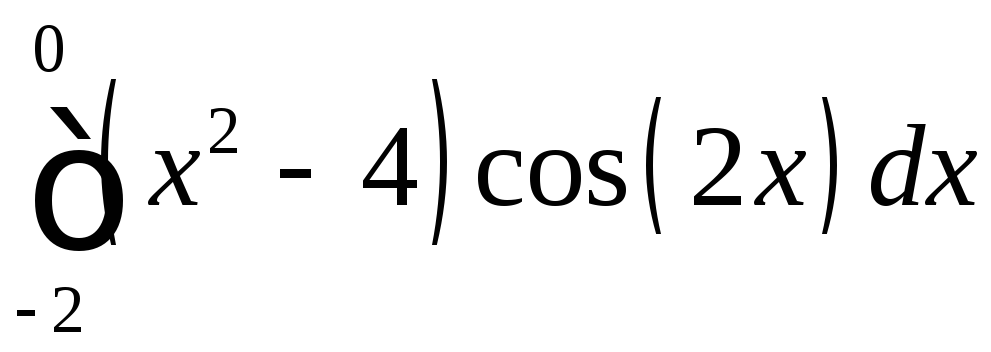
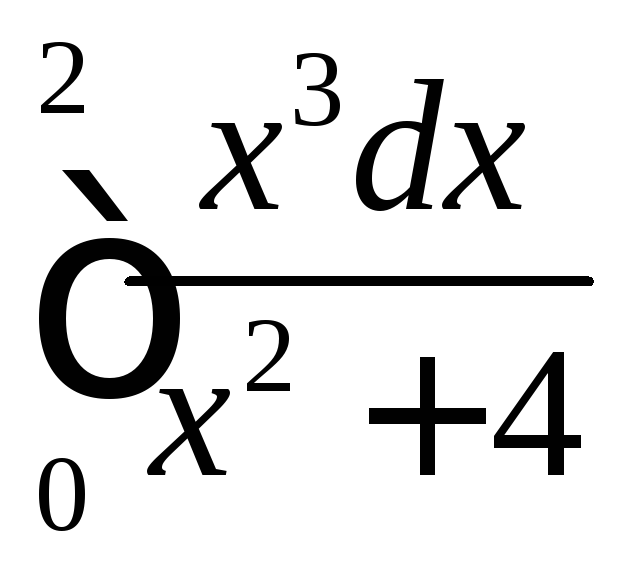
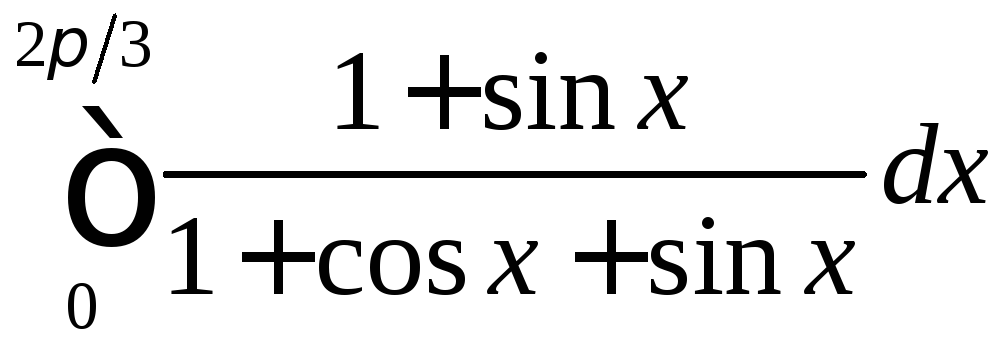
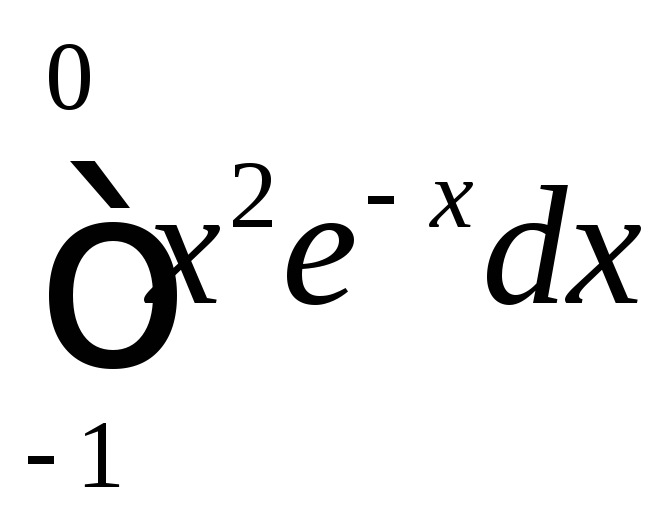
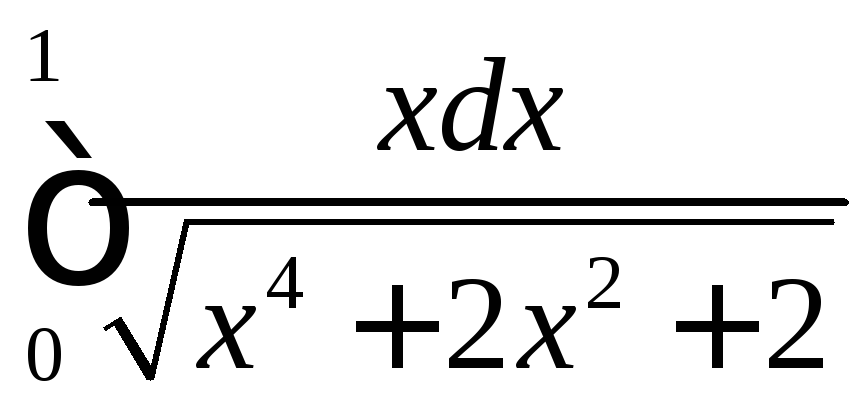
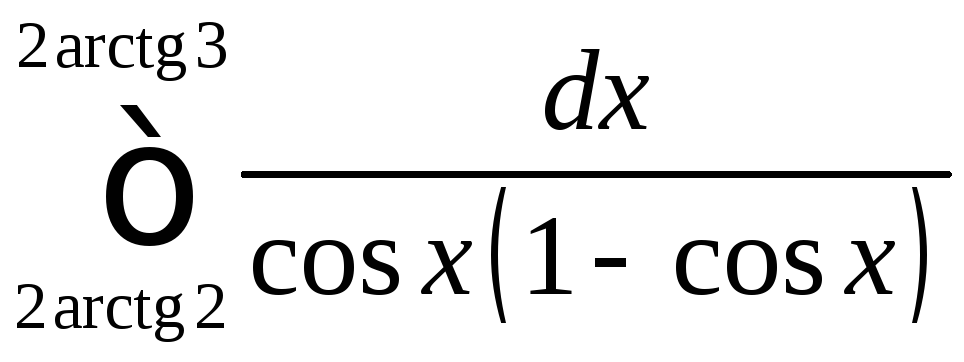
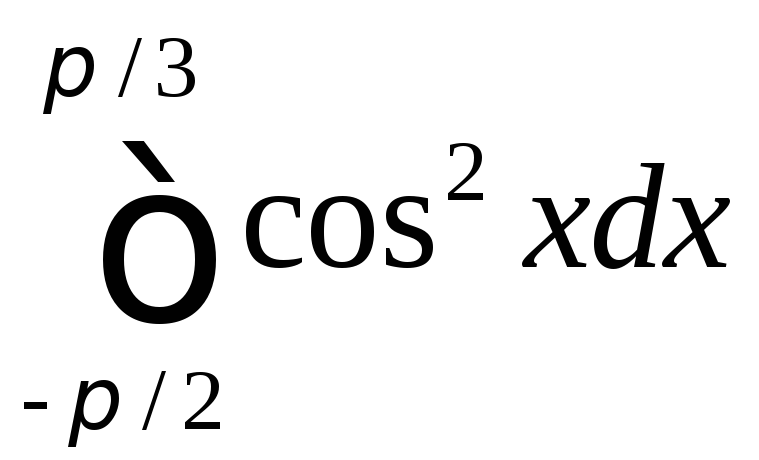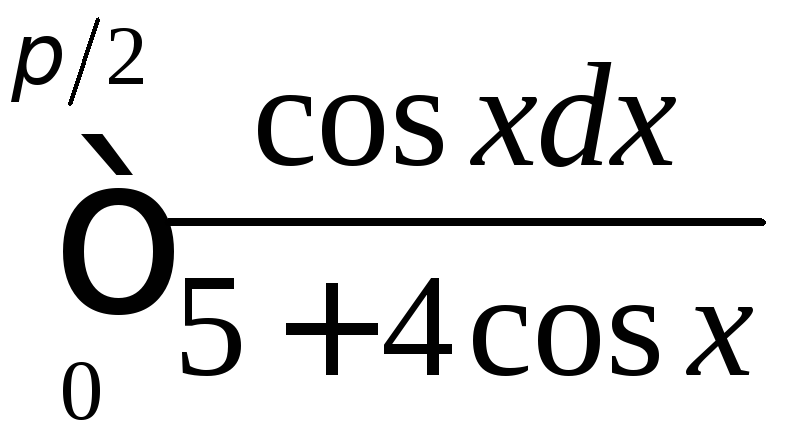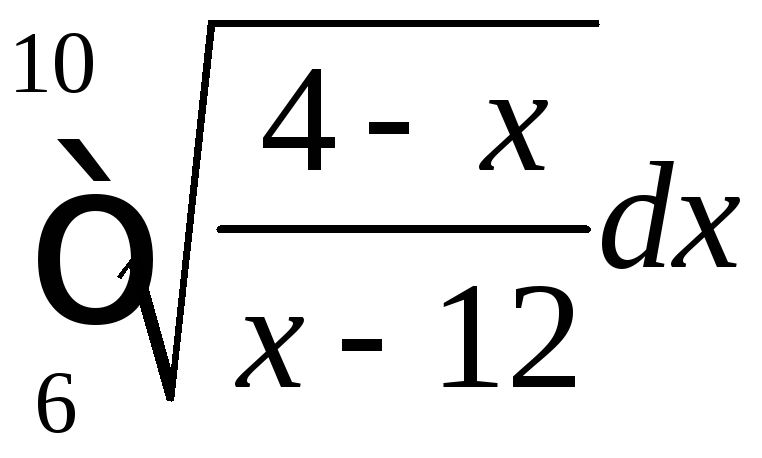
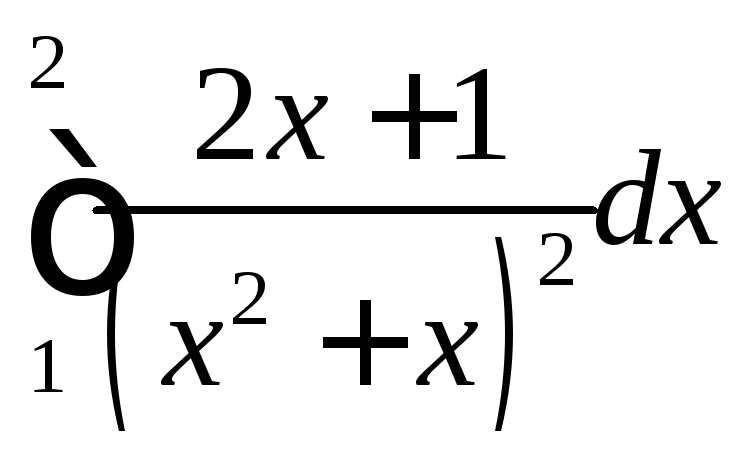
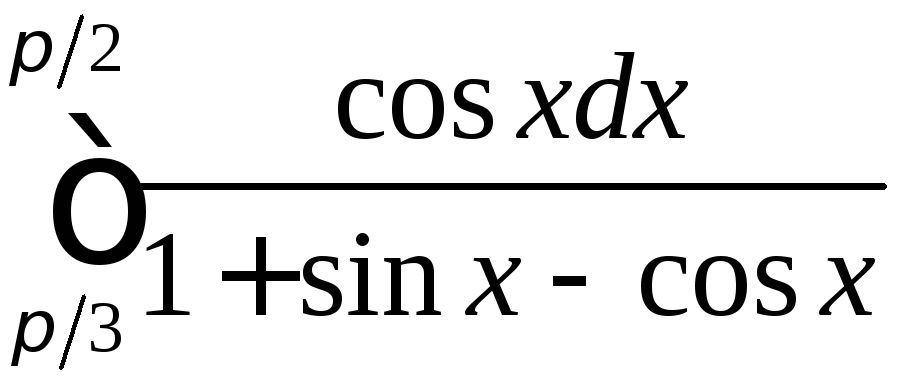
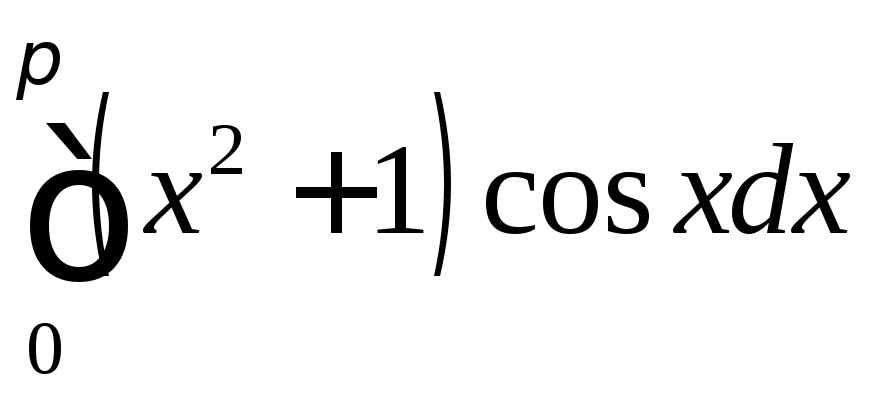
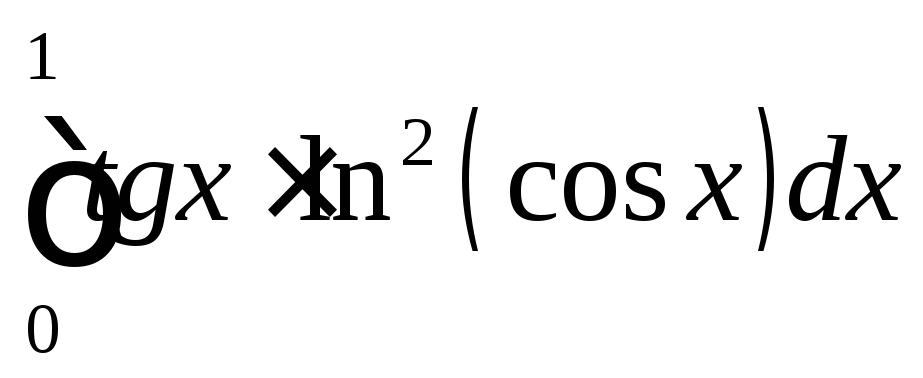
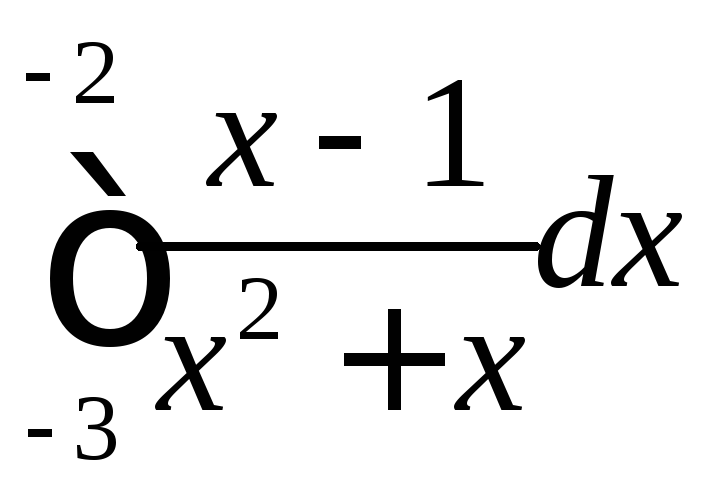
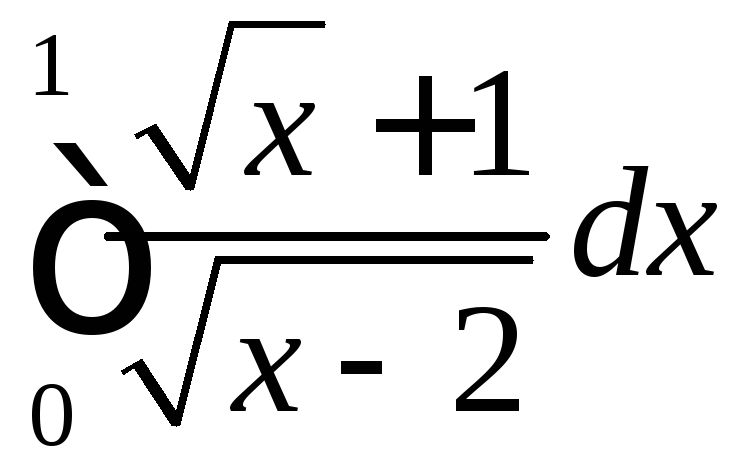
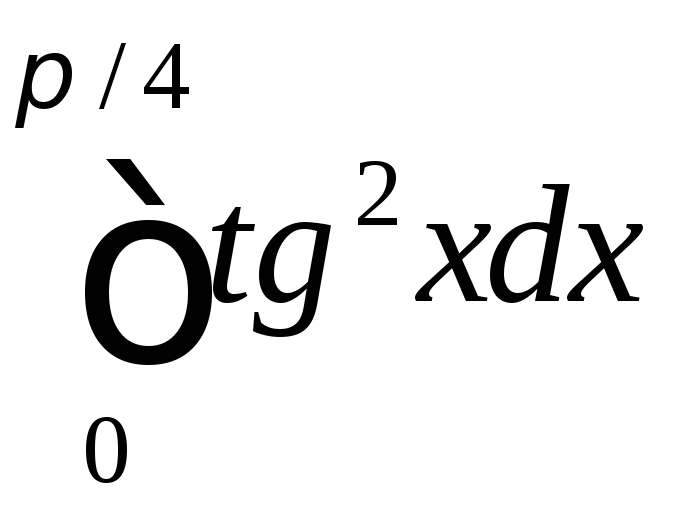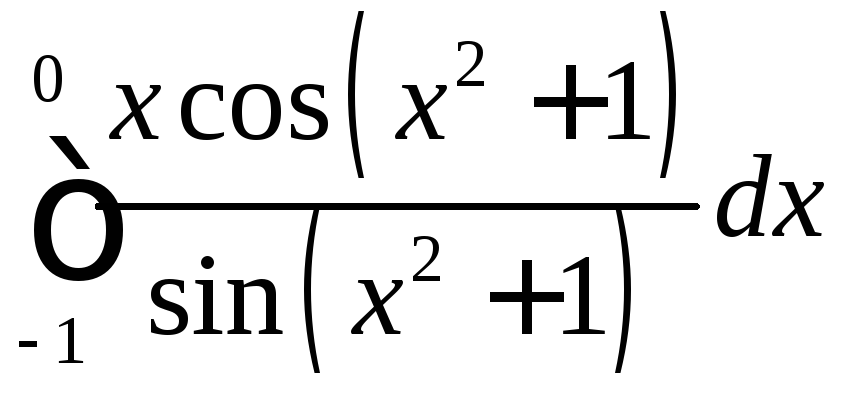
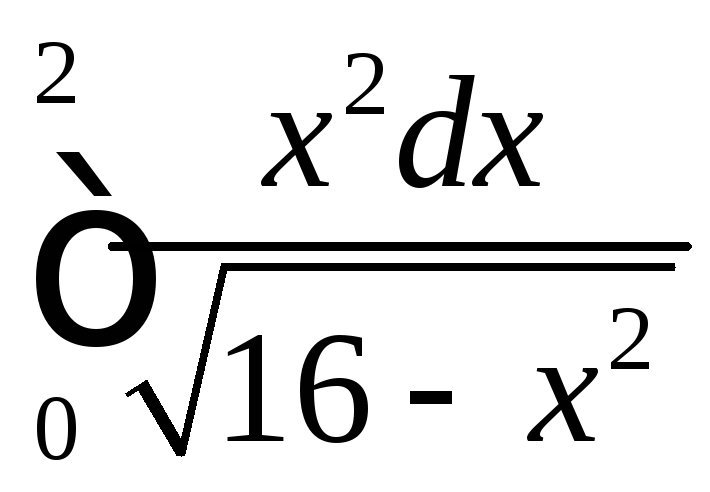
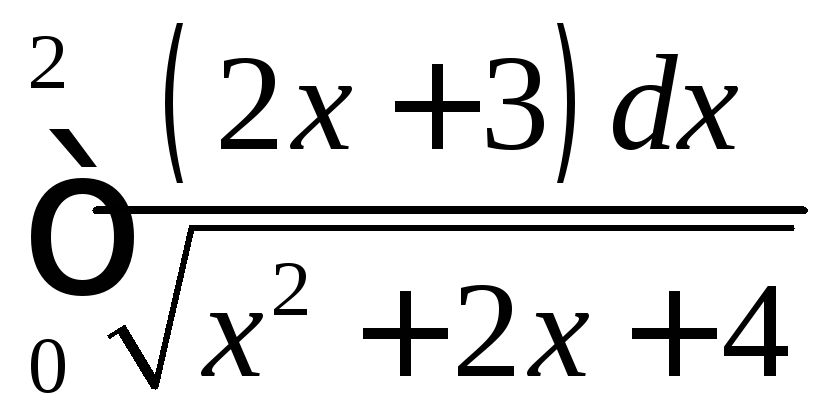
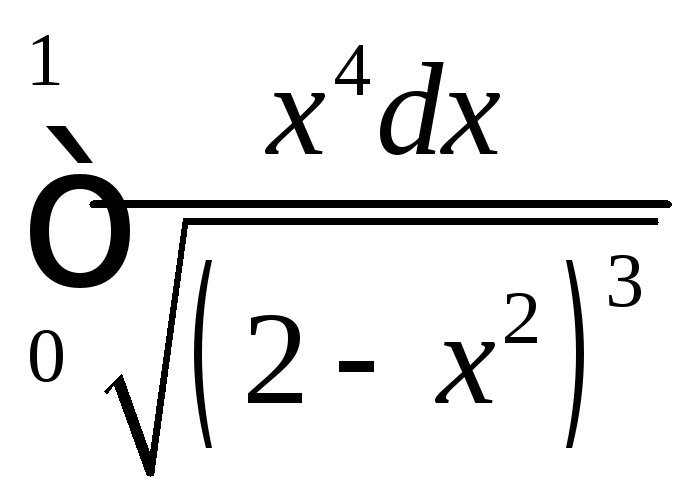
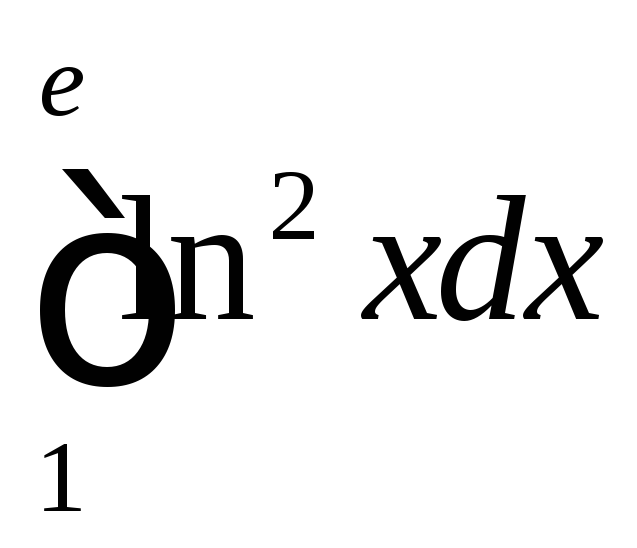
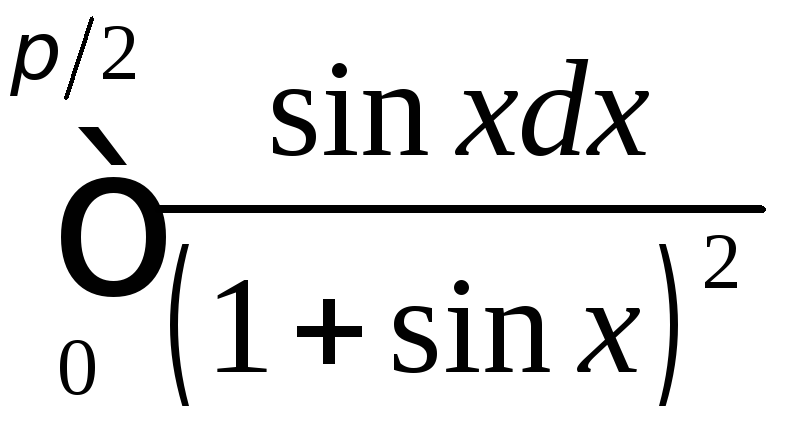
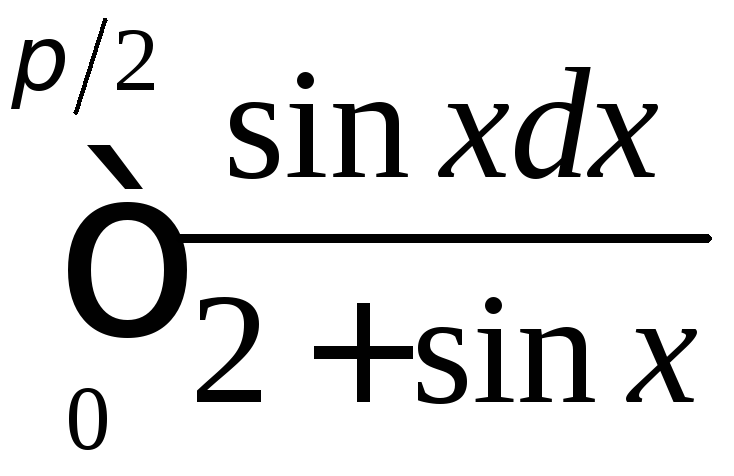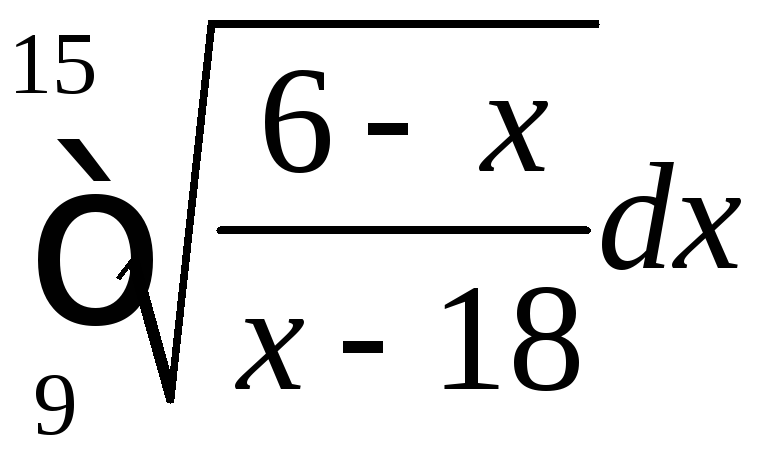
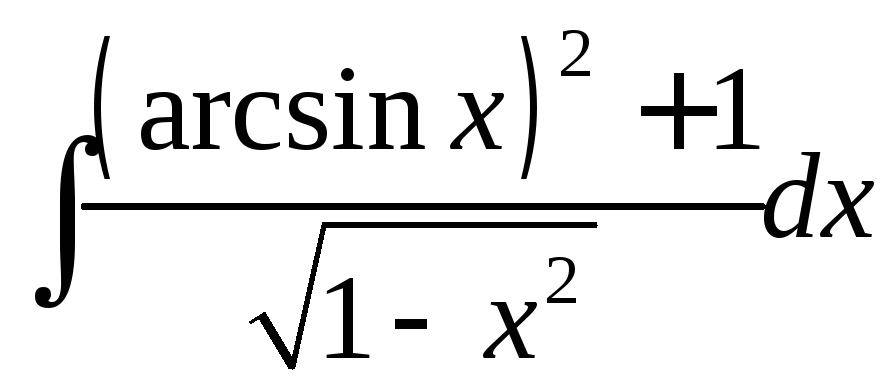
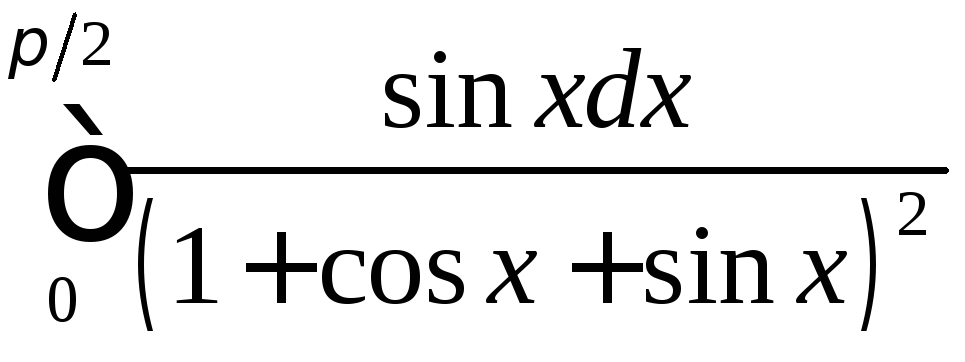
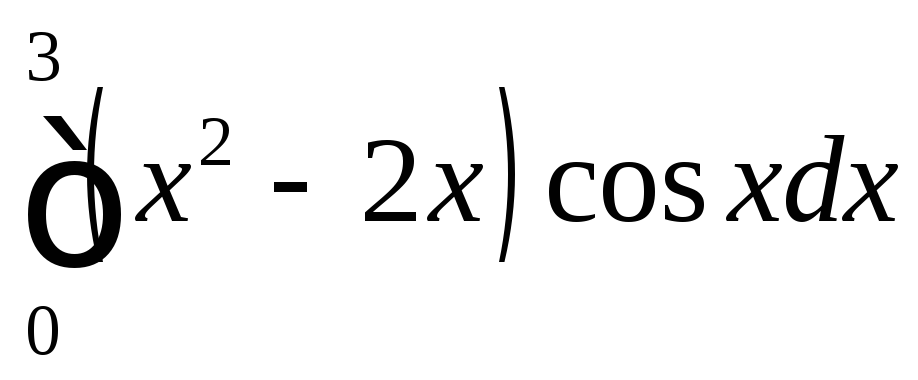
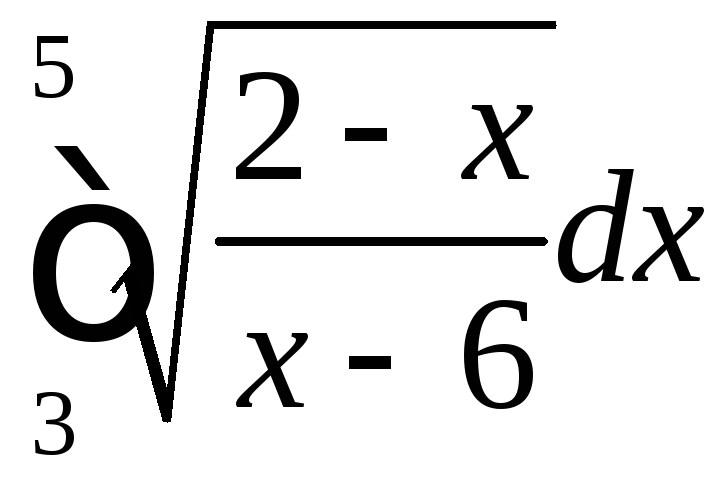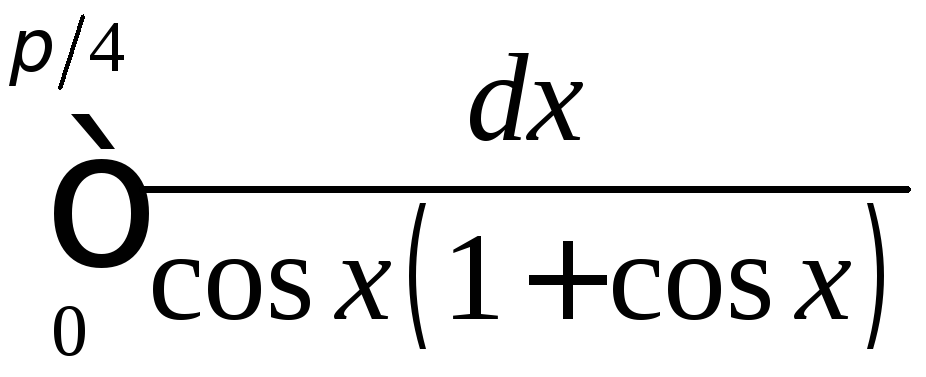
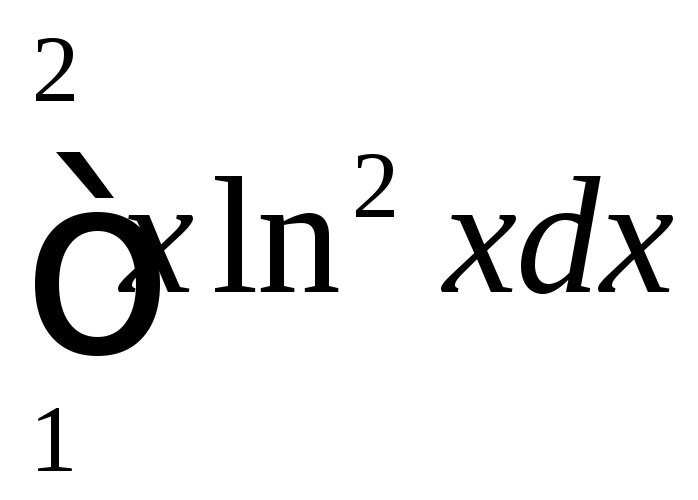
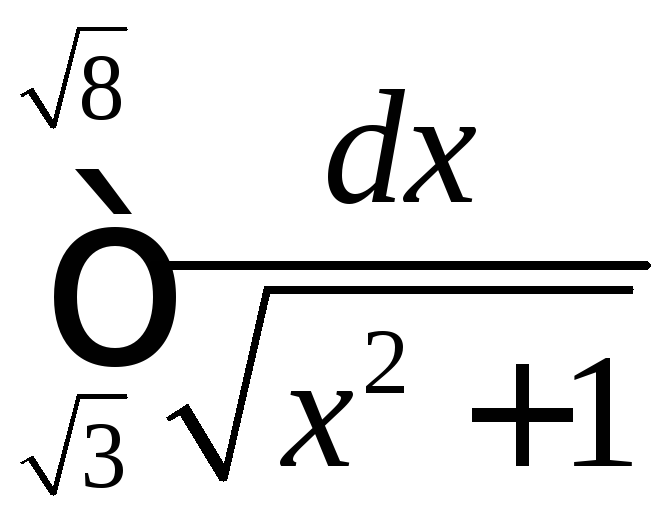
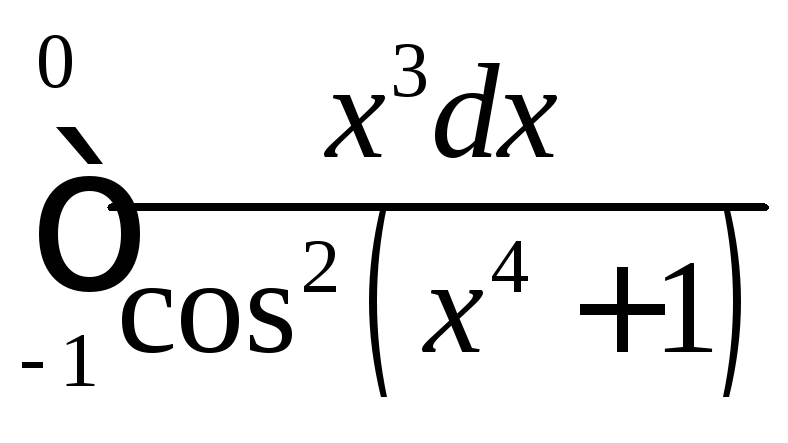
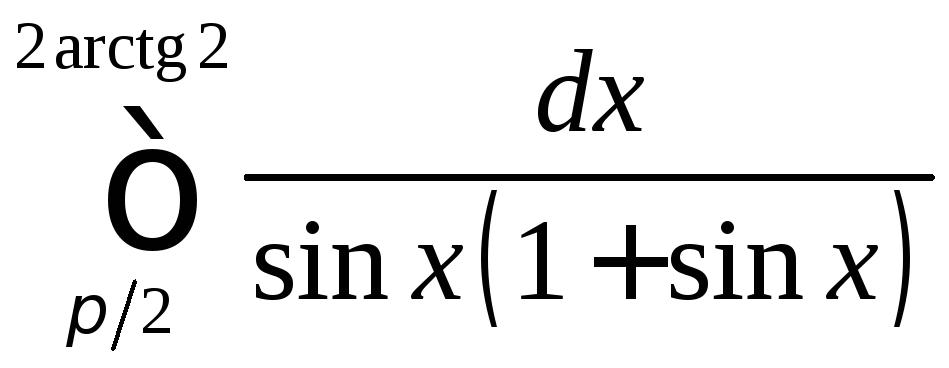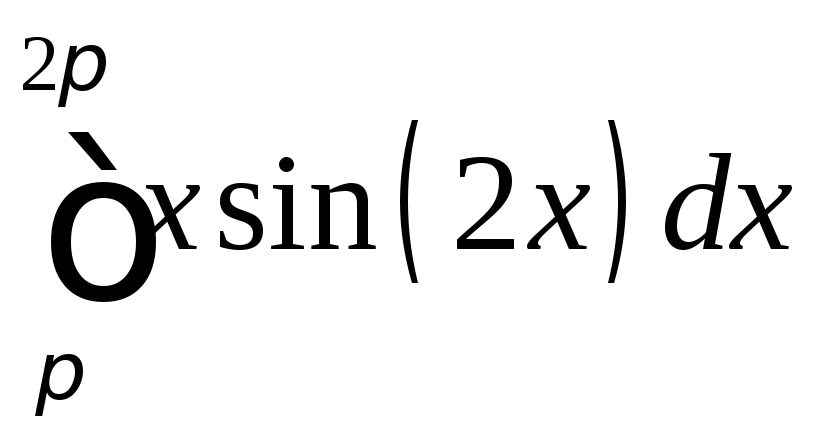
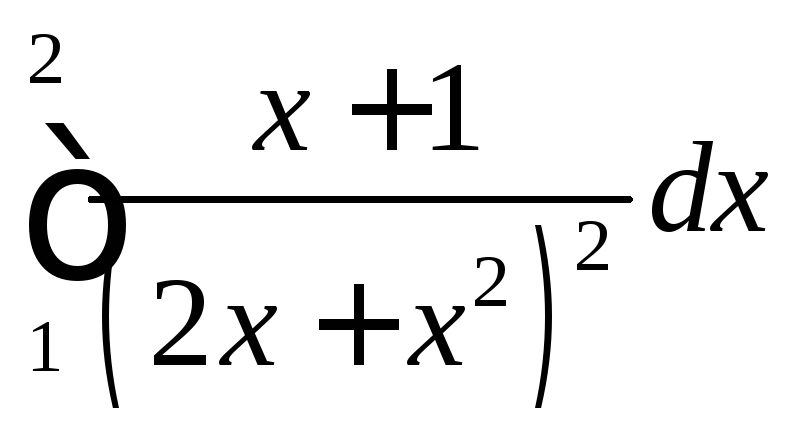
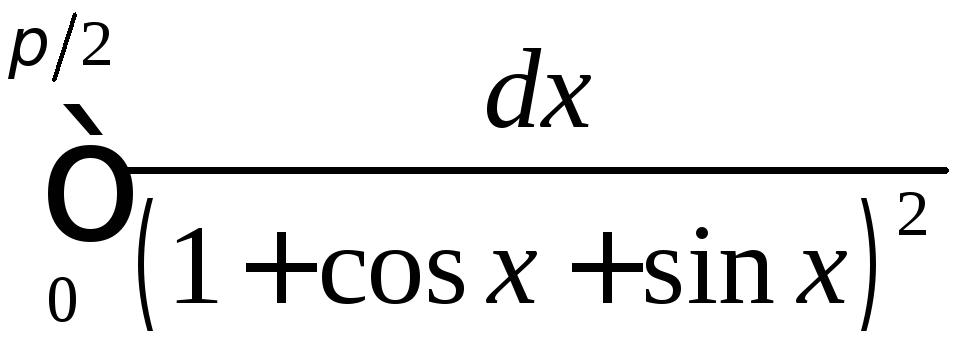
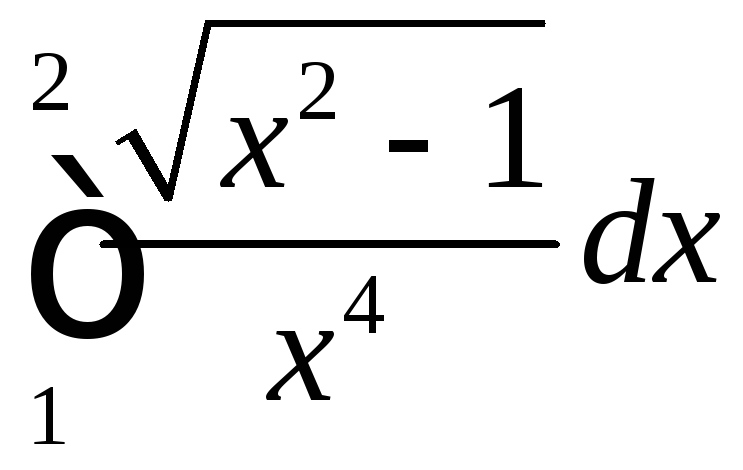
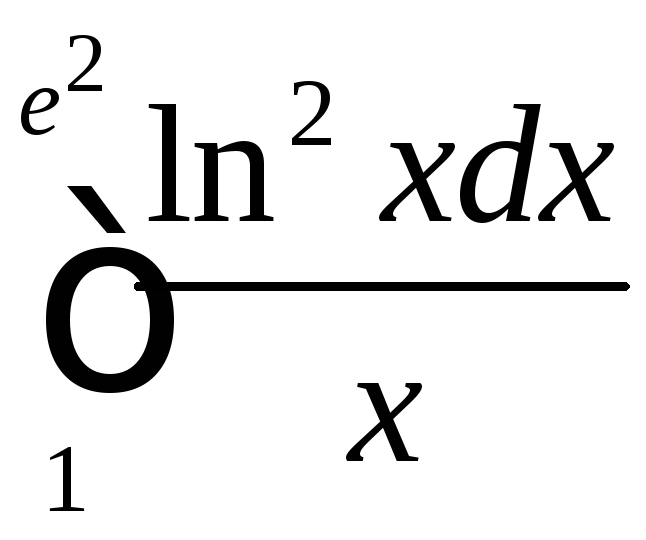
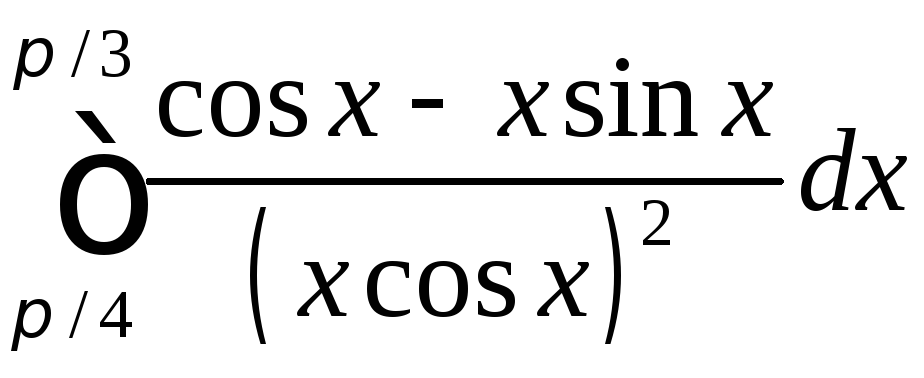
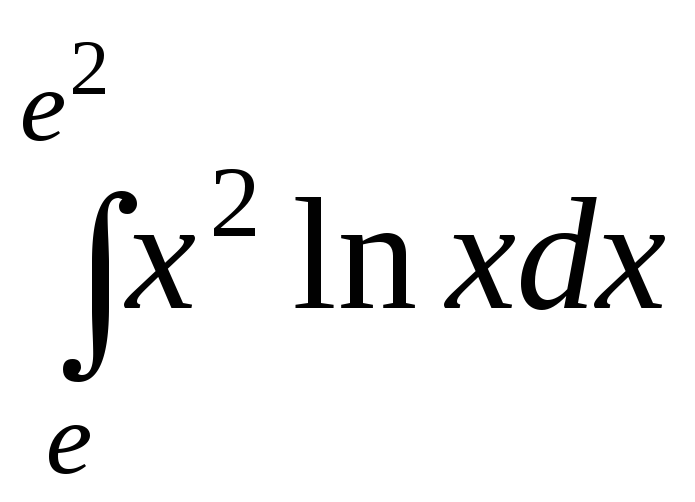
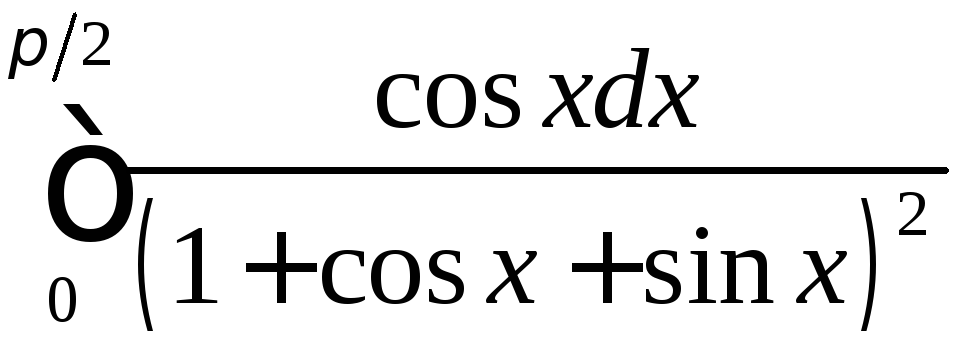
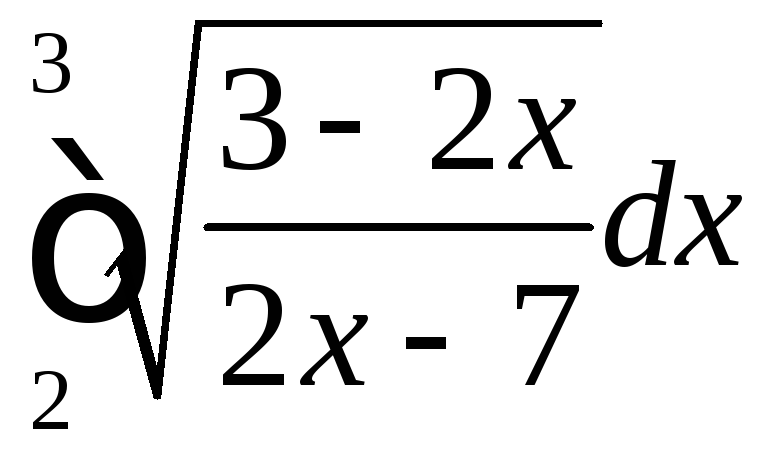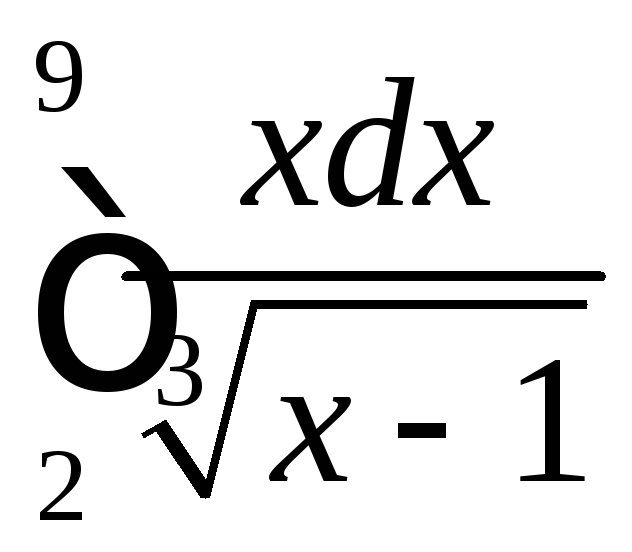
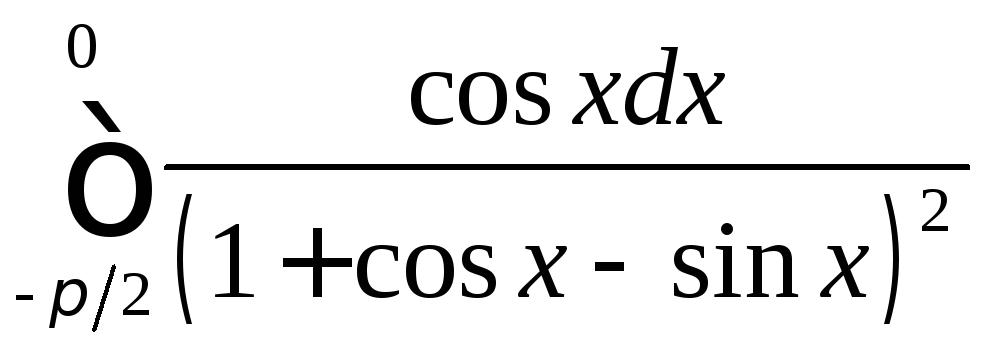
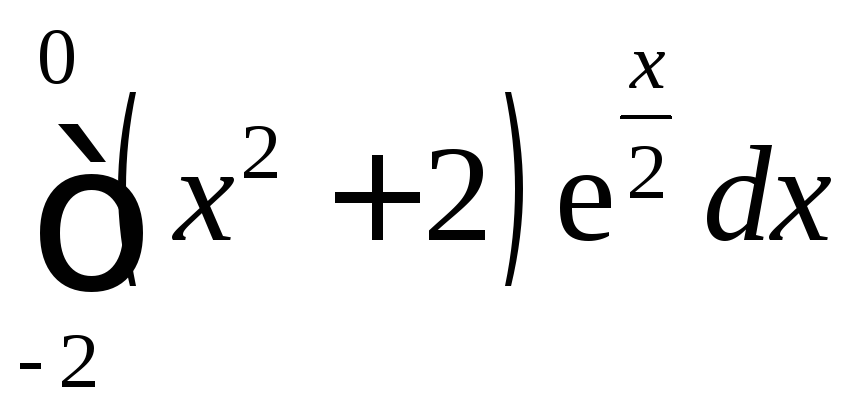
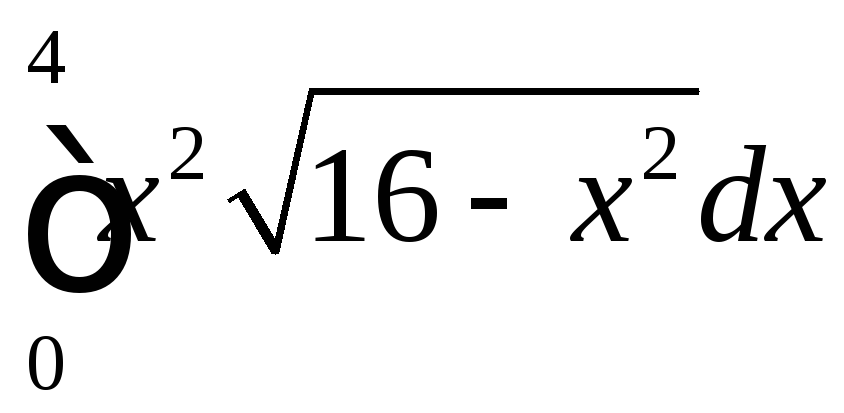
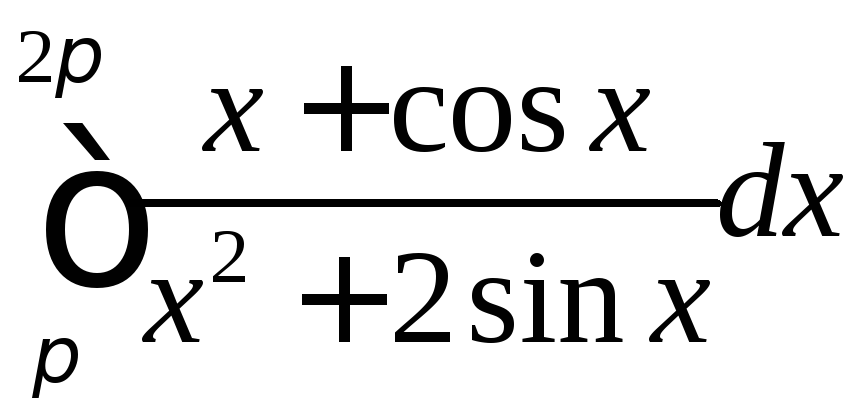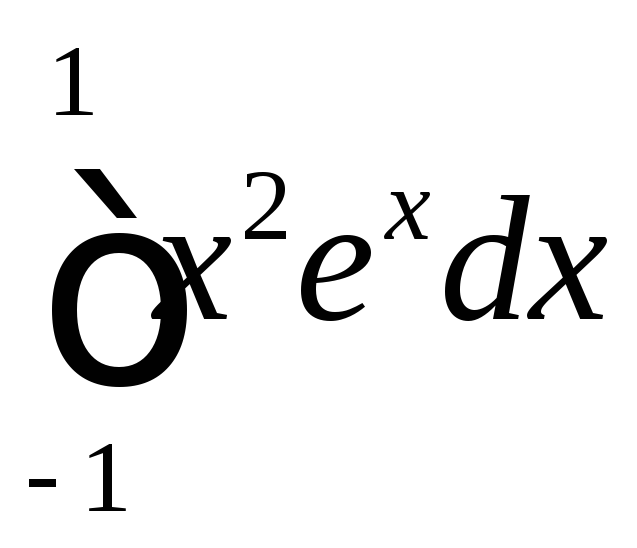
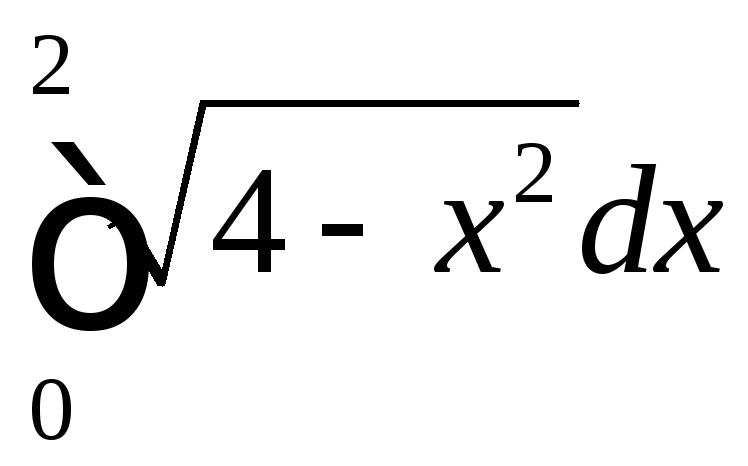
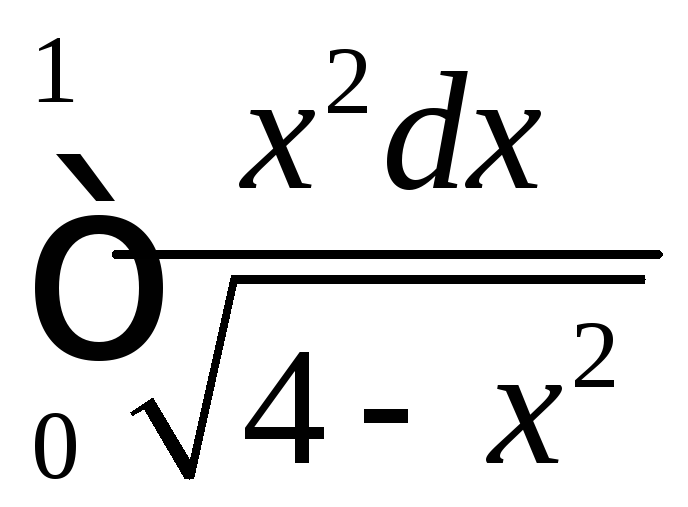
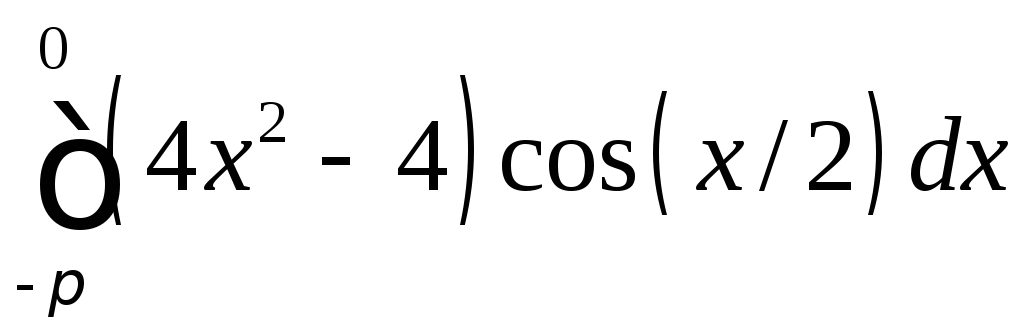
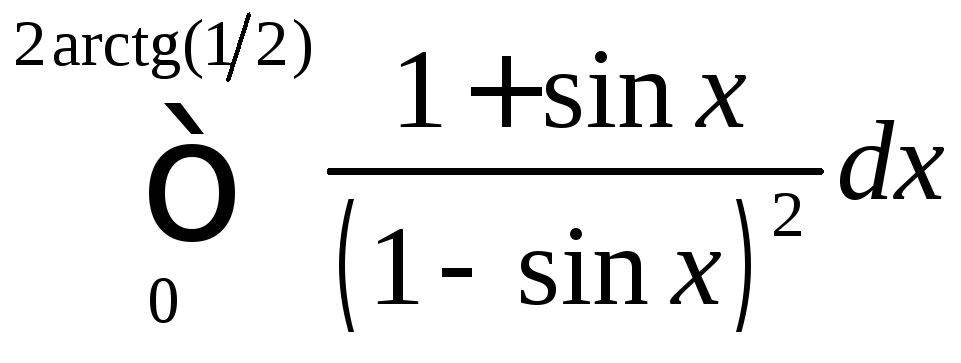
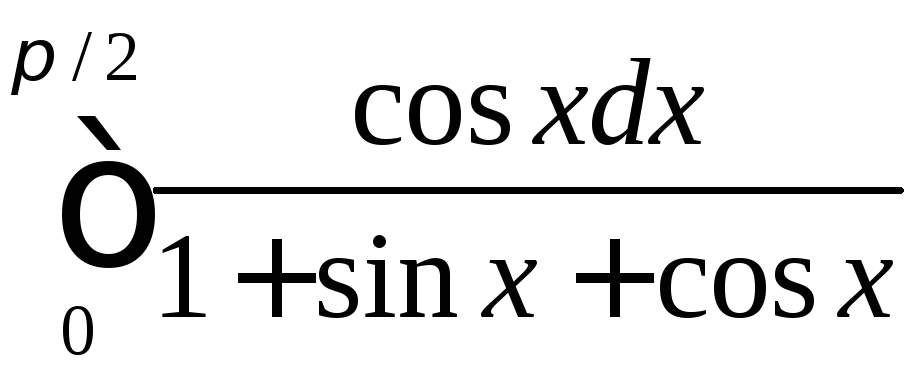
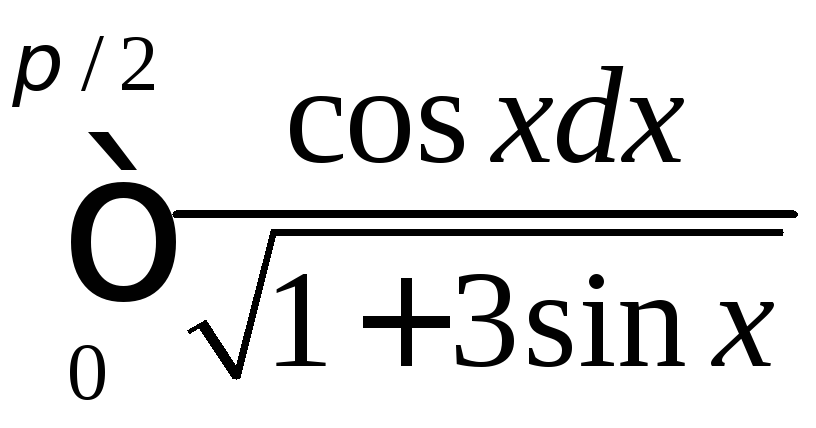
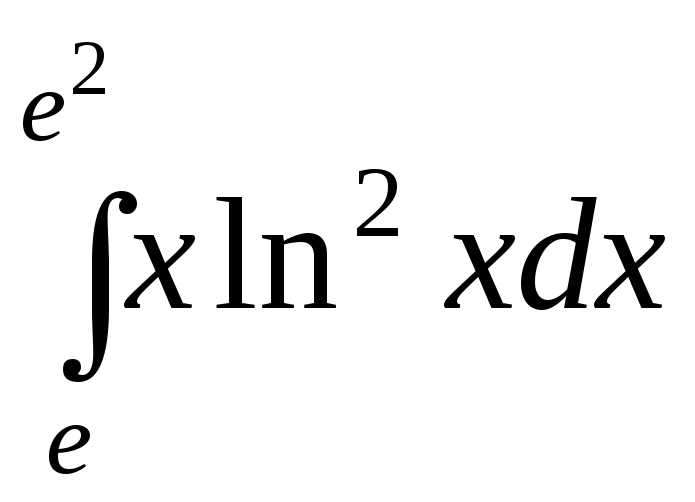
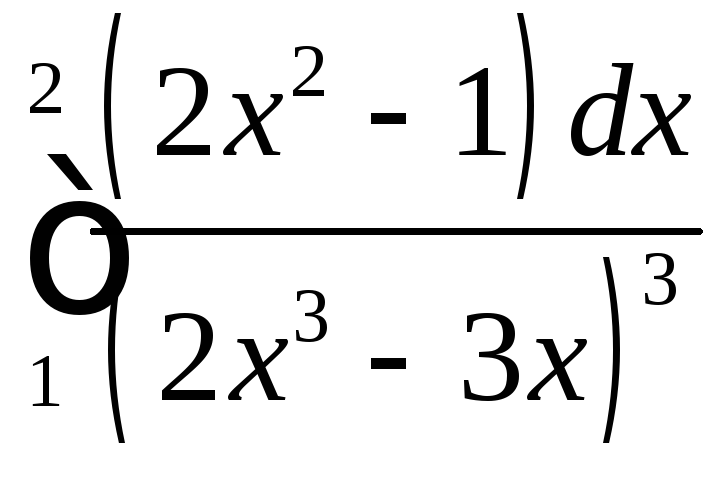
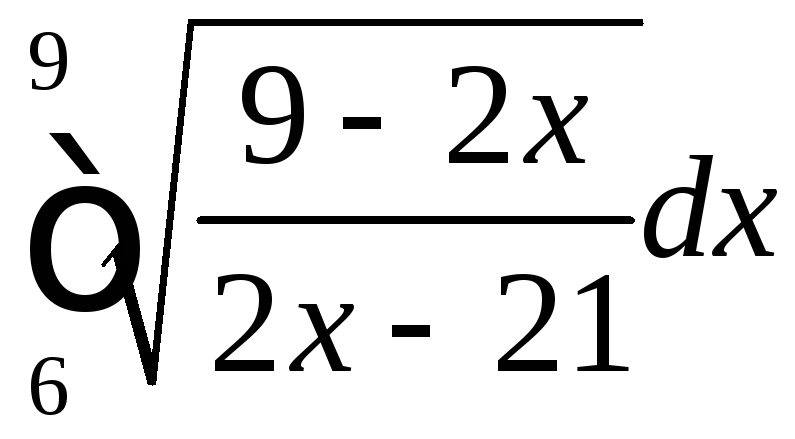
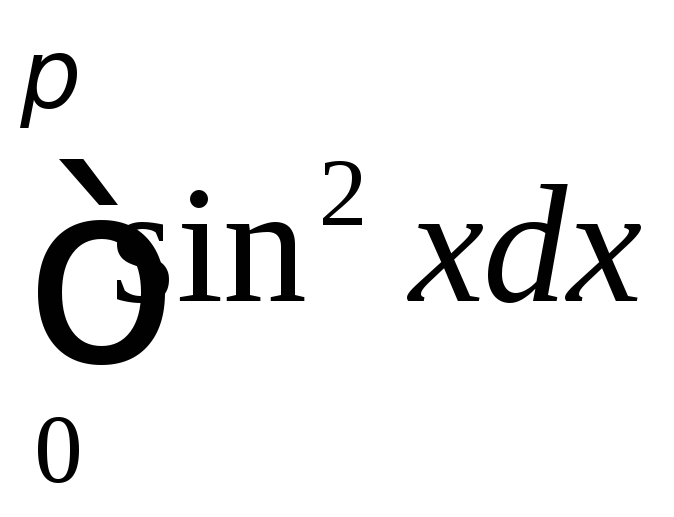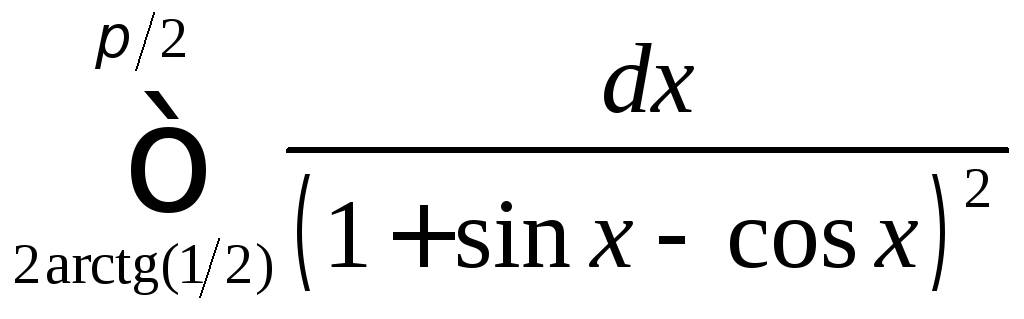
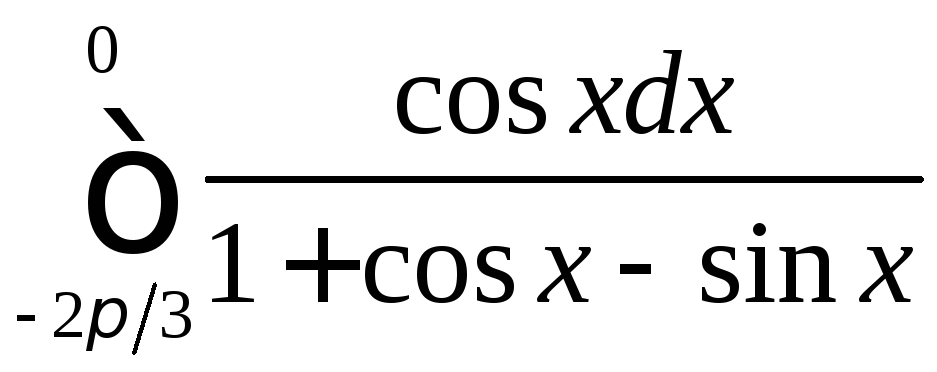
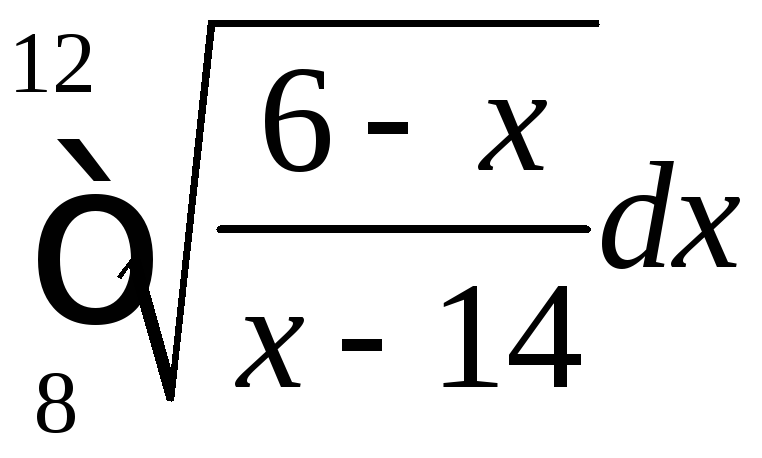
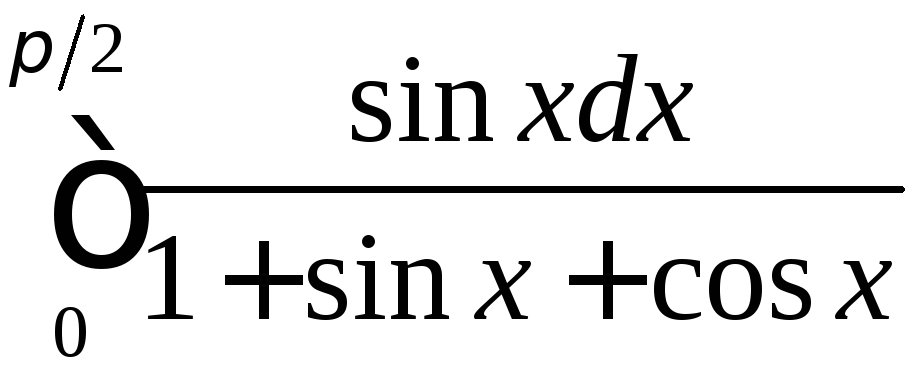
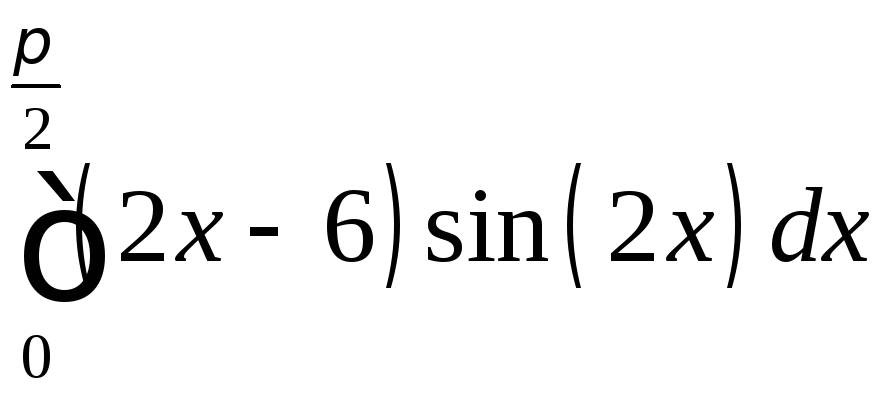
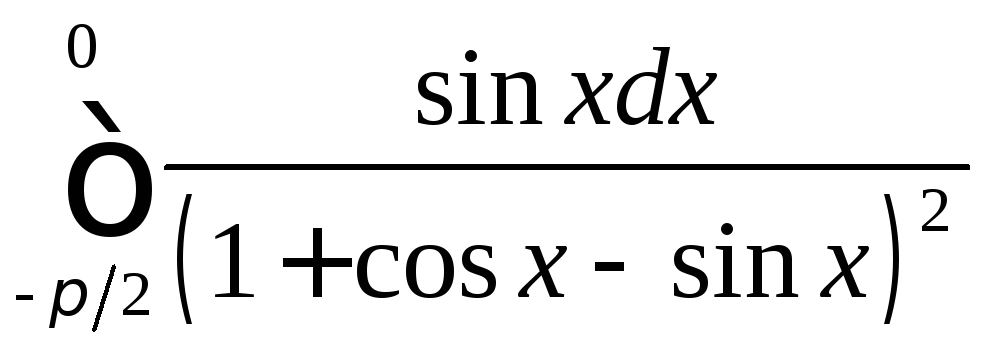
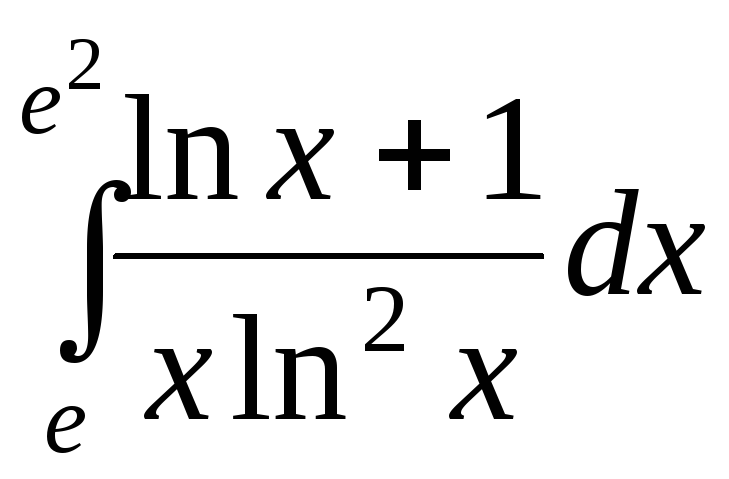
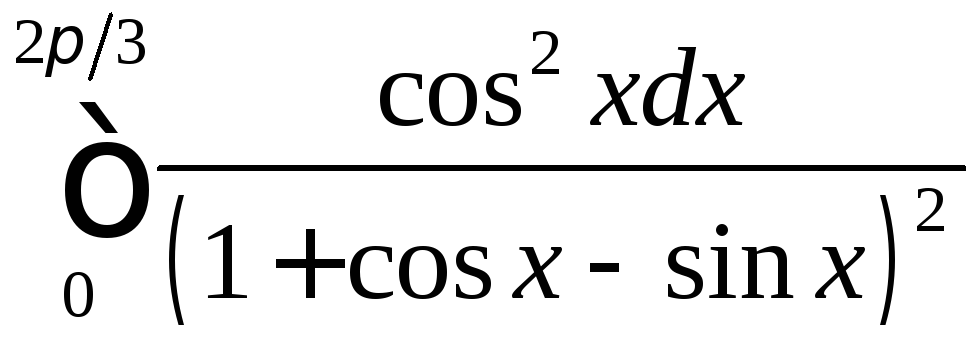
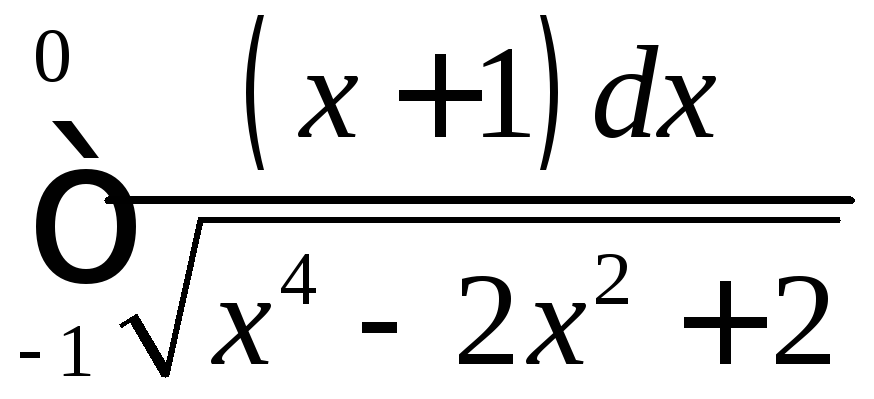
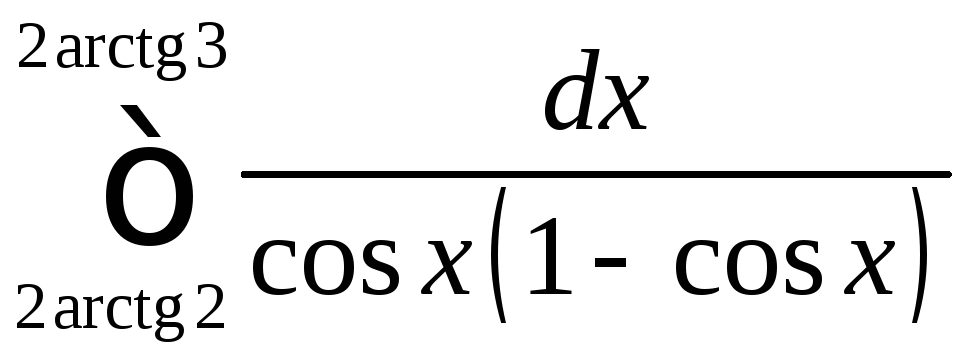
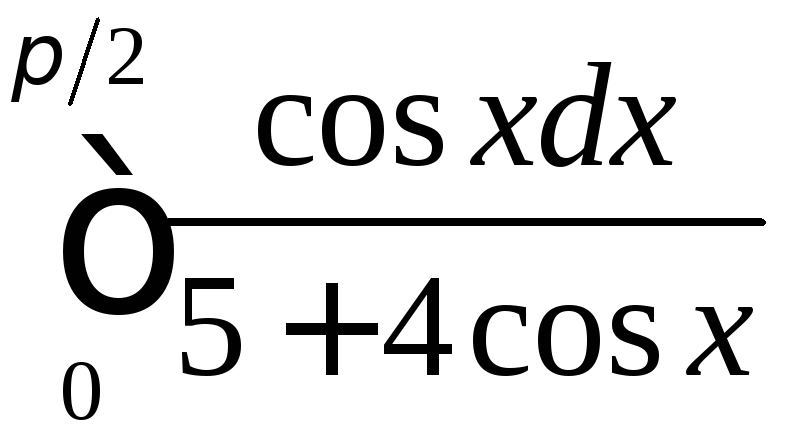
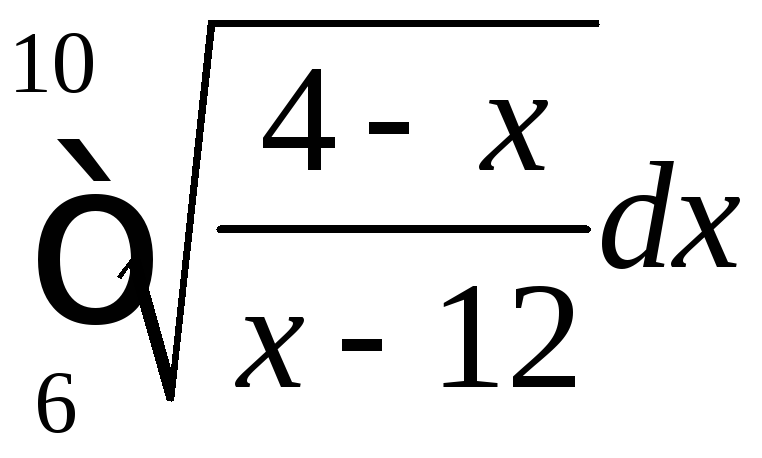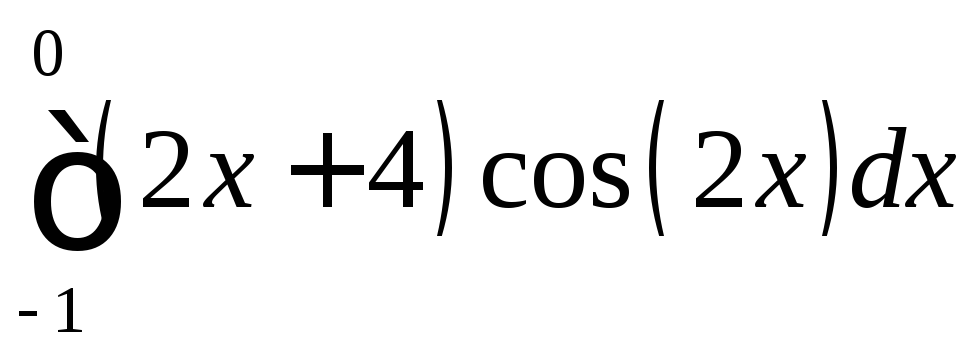
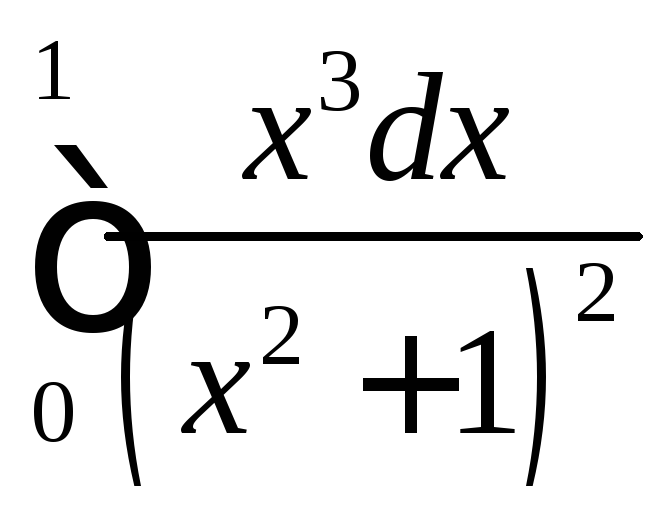
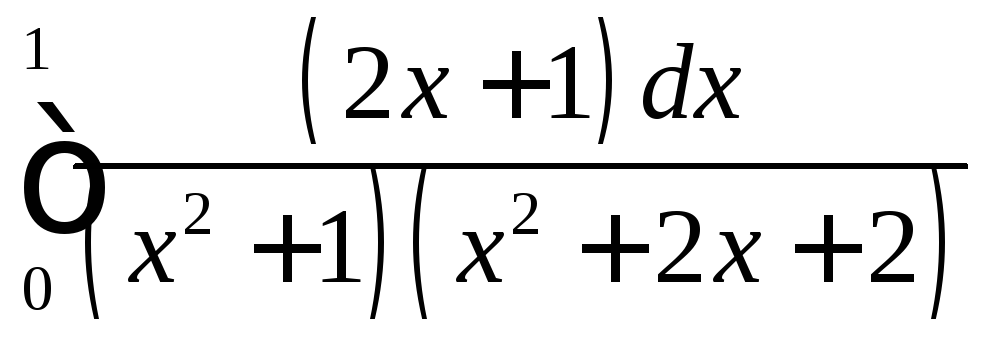
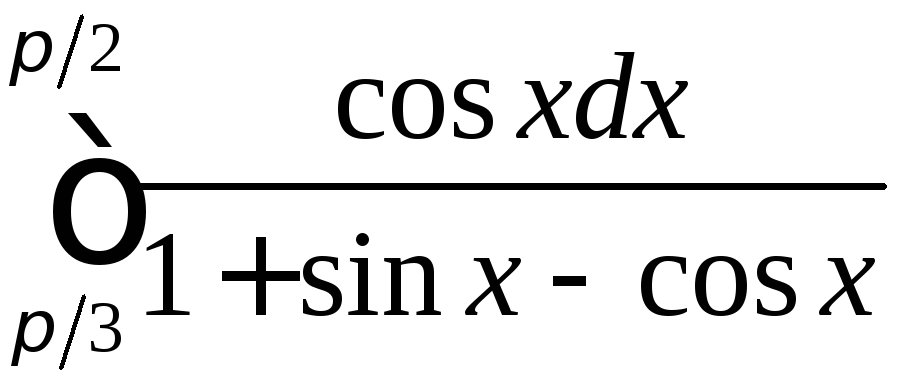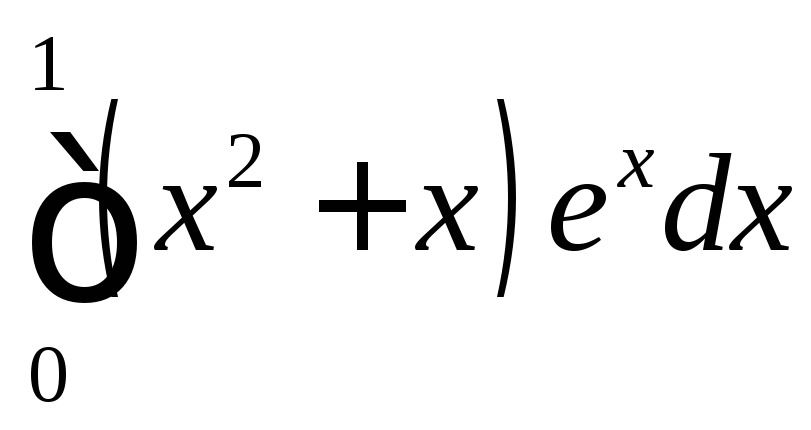
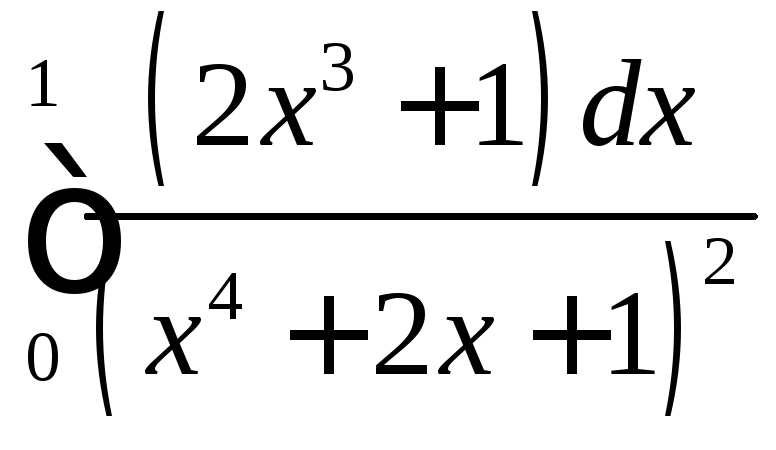
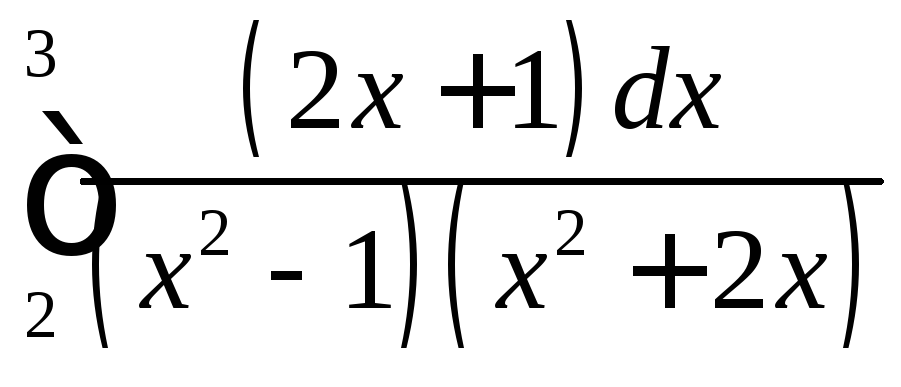
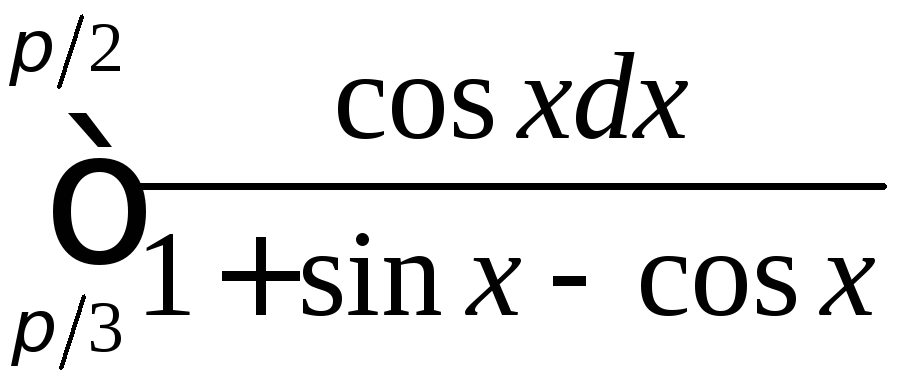
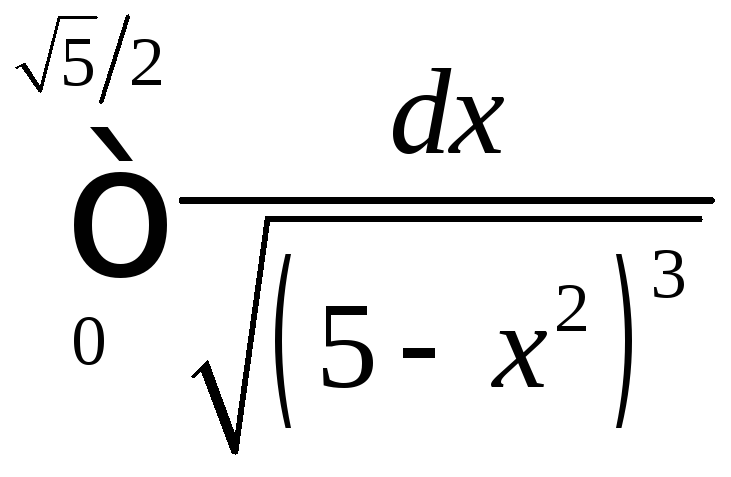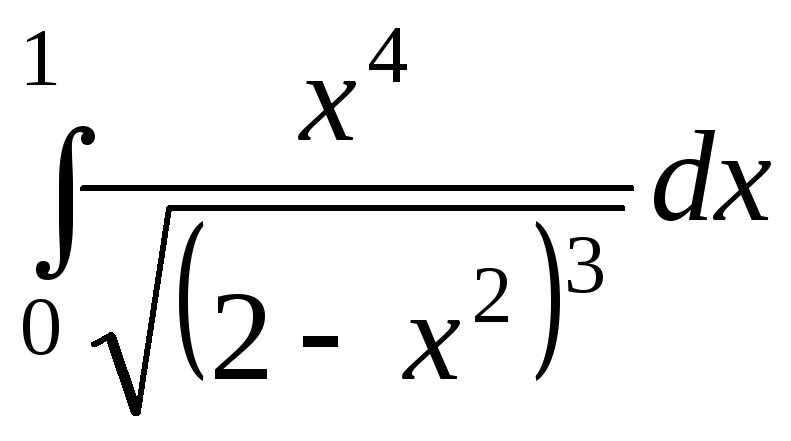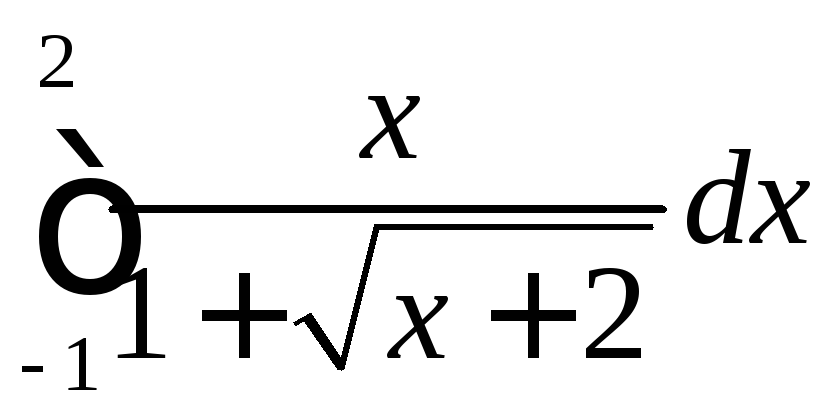
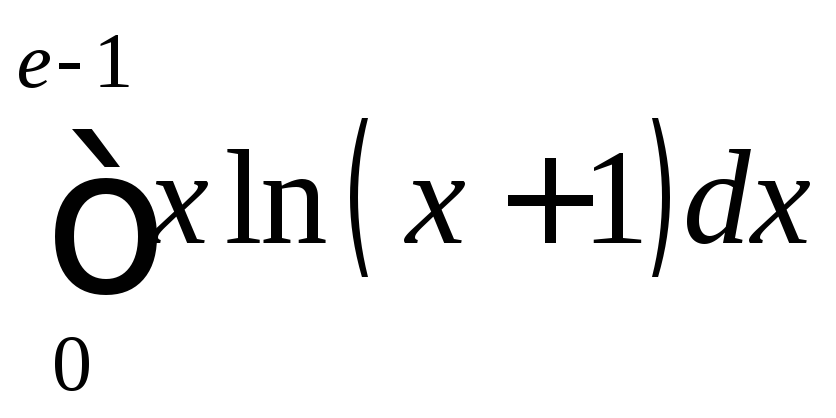
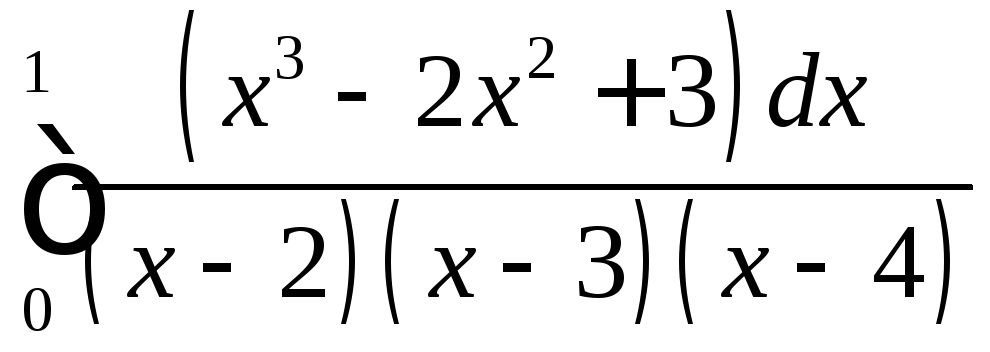
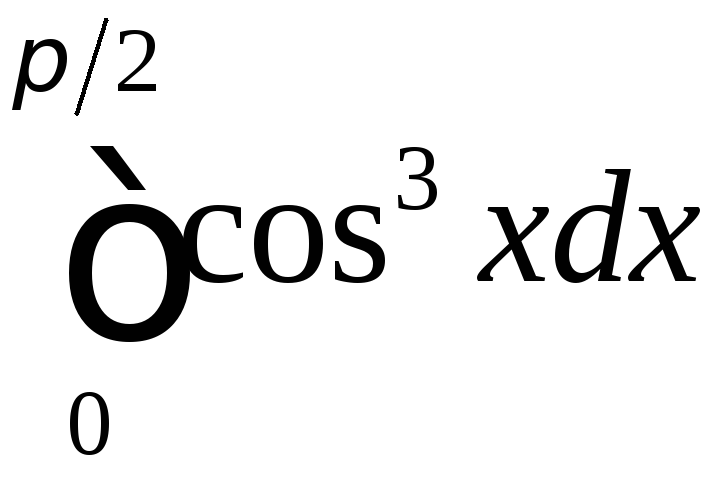
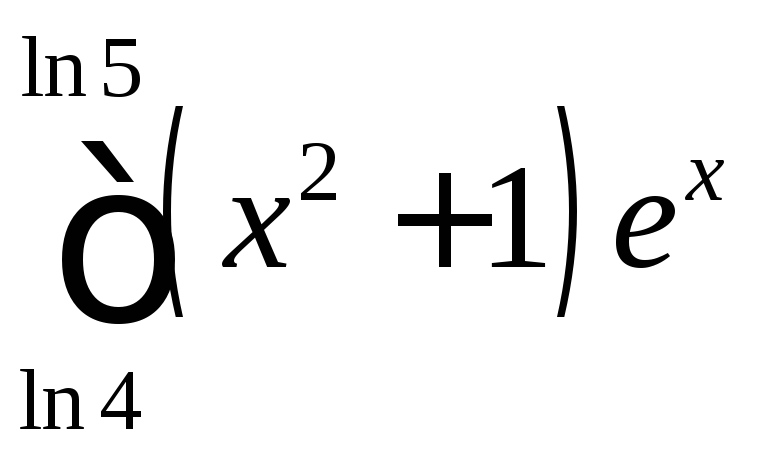
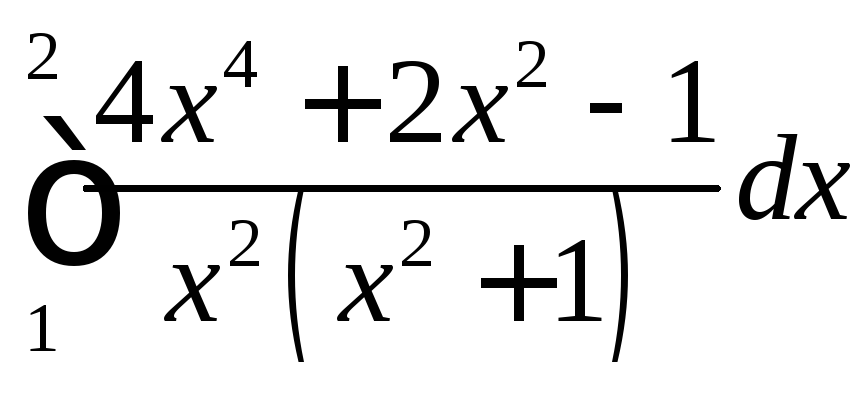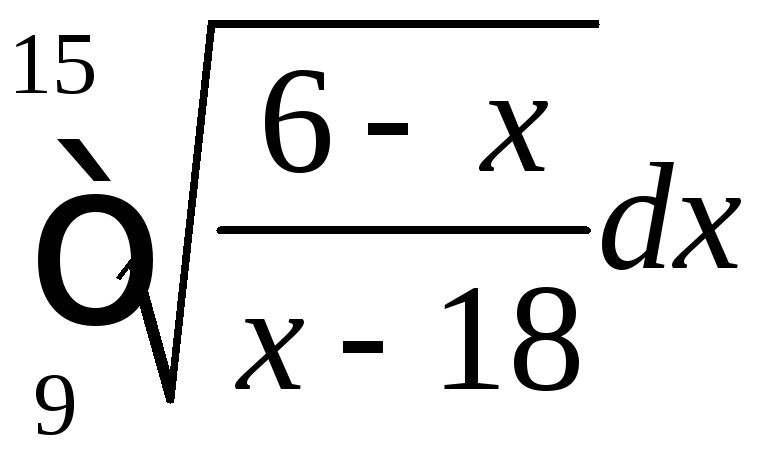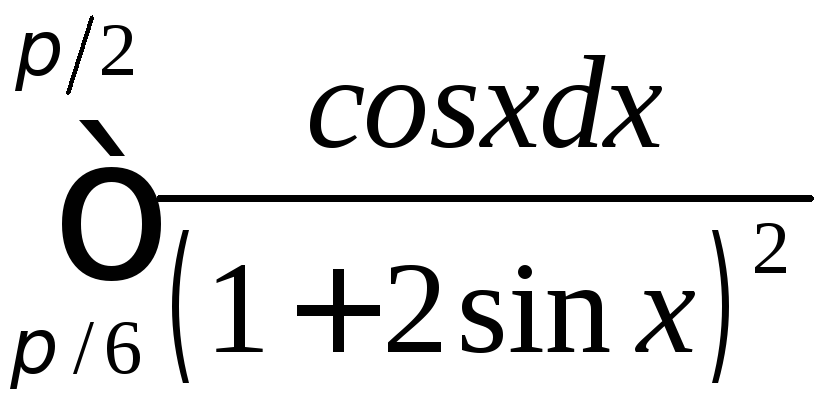
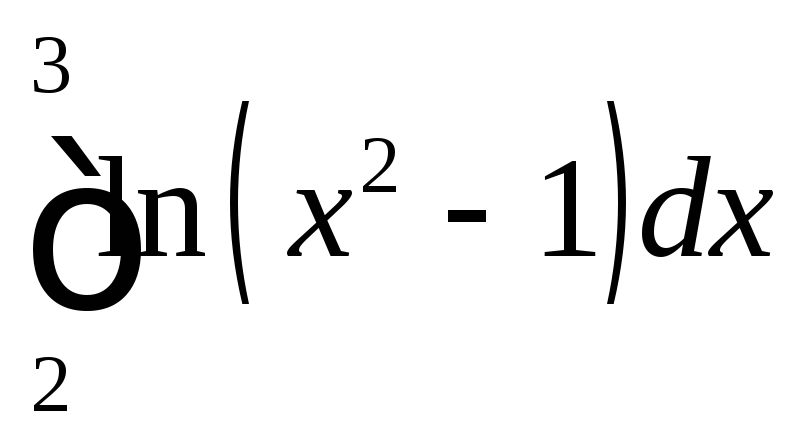
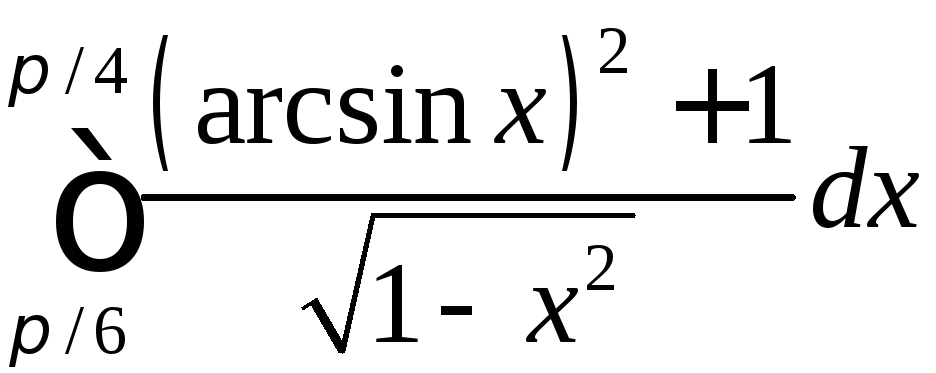
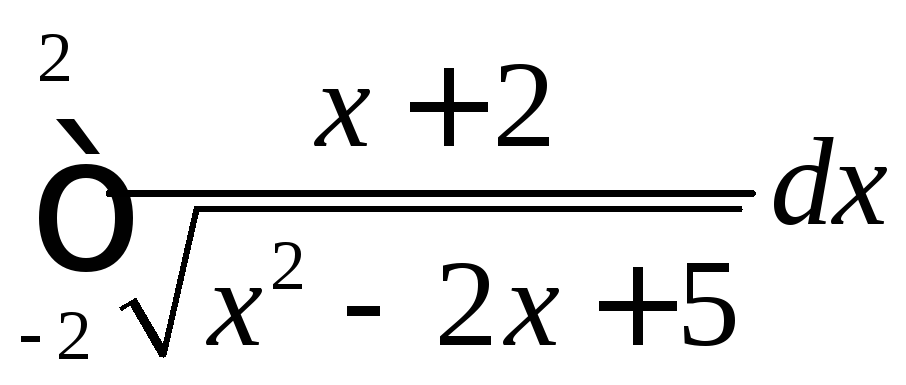
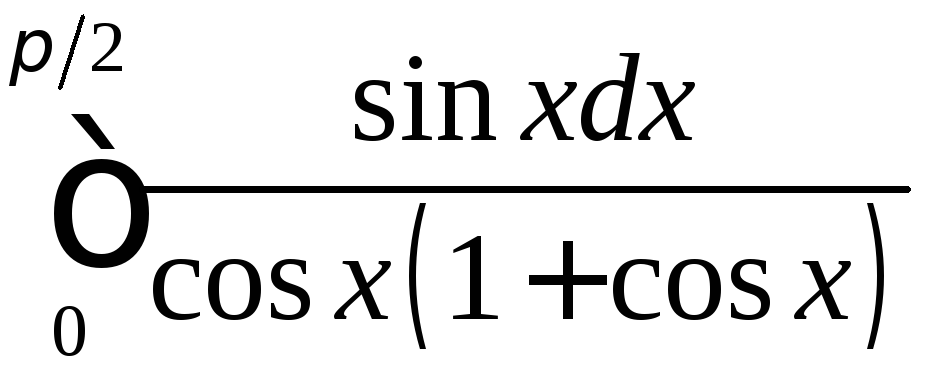
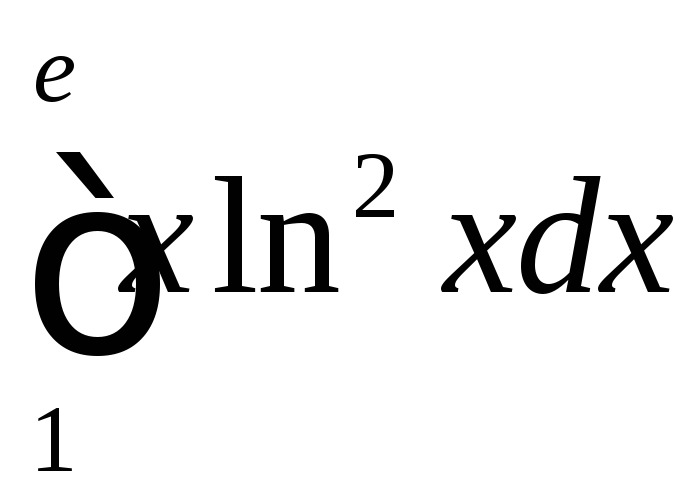
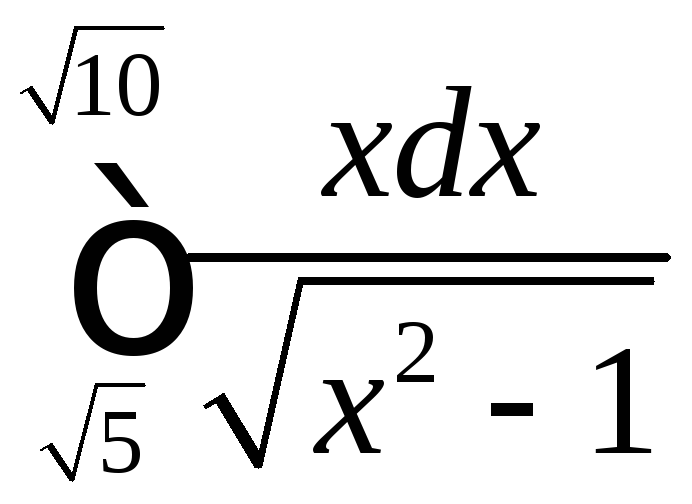
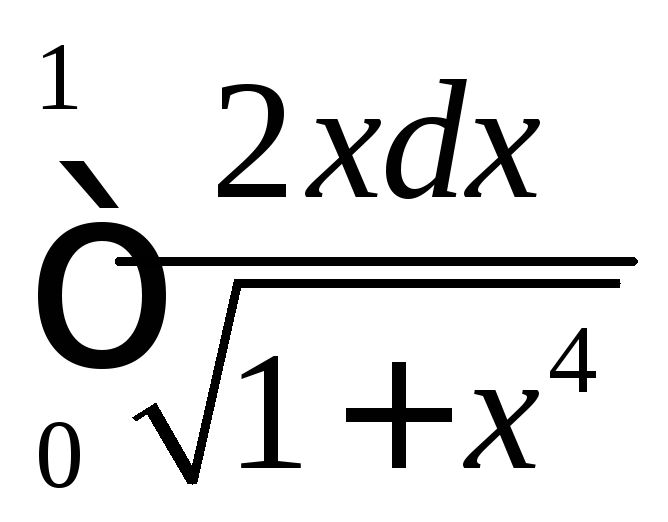
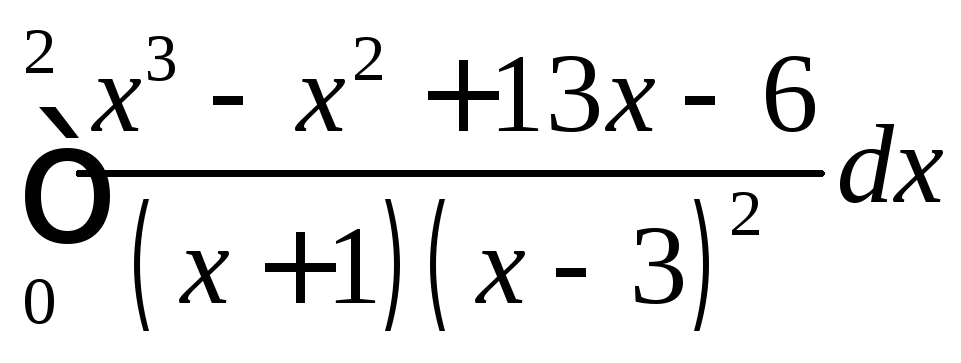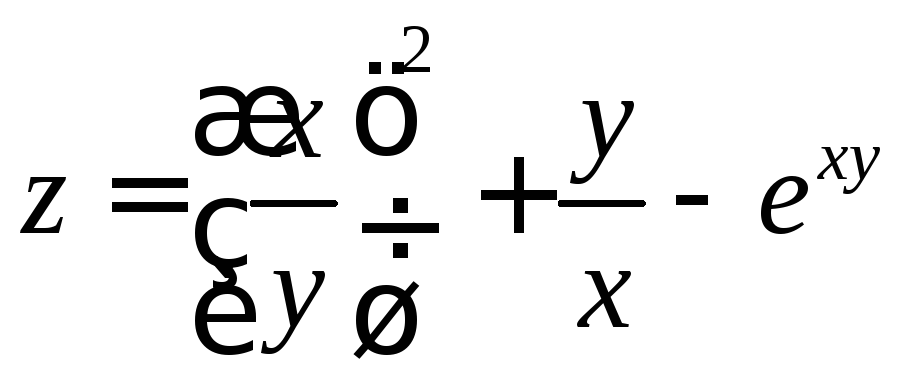
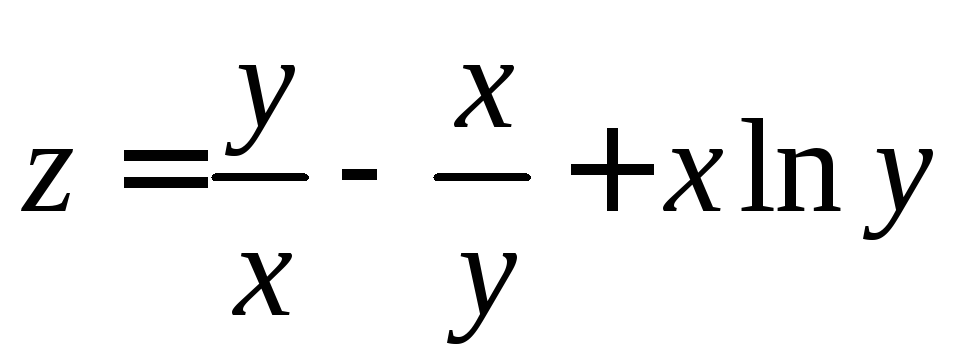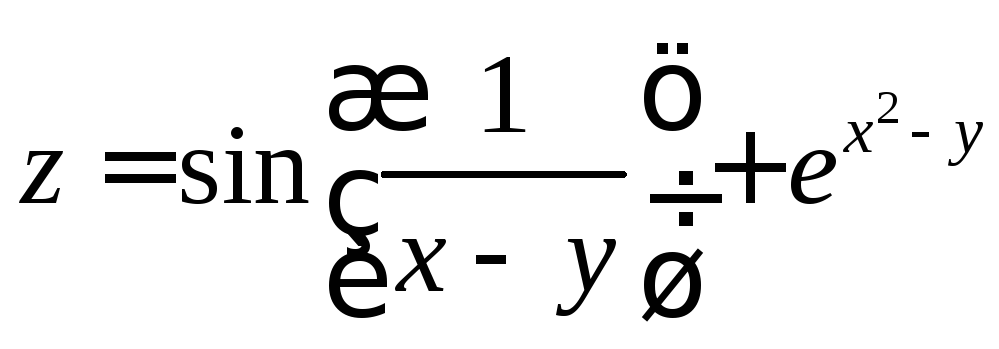
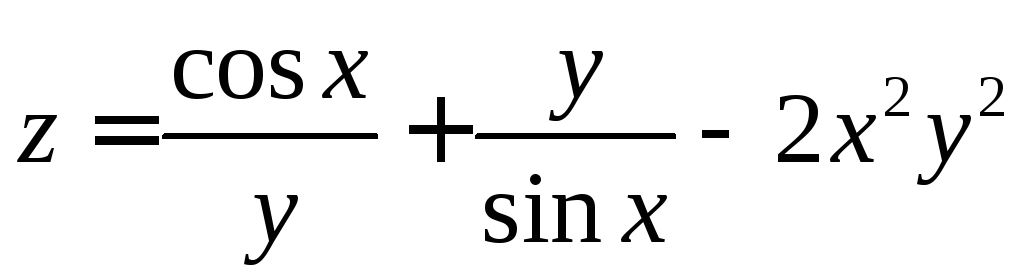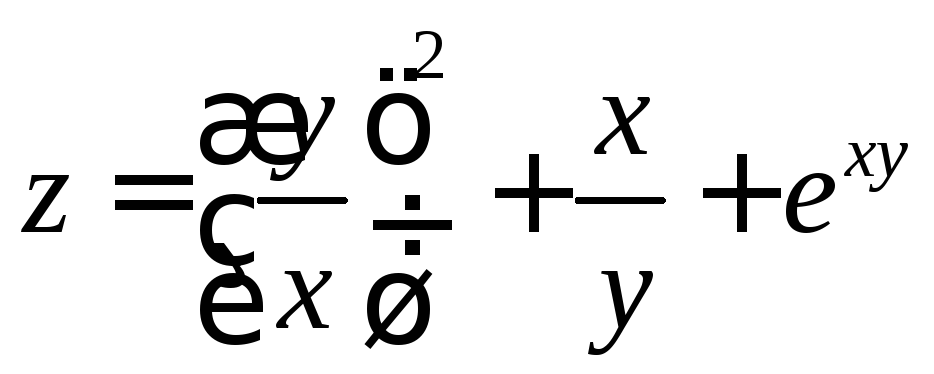
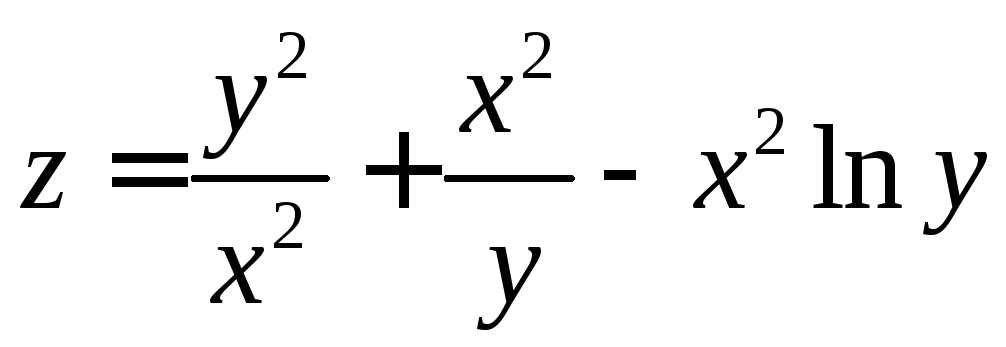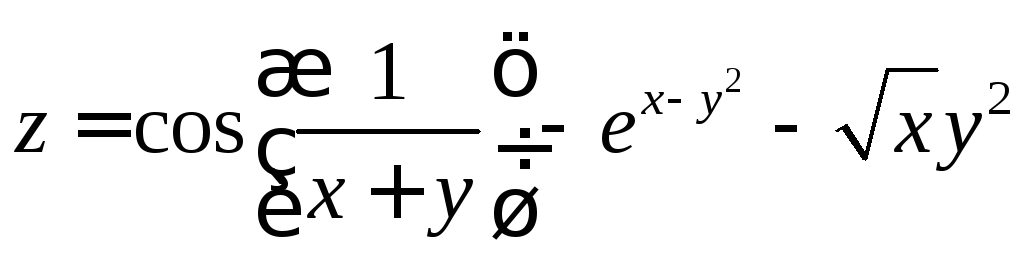