11

Глава 2. Детерминированные радиотехнические сигналы

2.1. Математические модели детерминированных радиотехнических сигналов

Детерминированные сигналы задаются аналитически и их параметры можно определить в любой момент времени.

К детерминированным сигналам относятся:

- Гармоническое колебание (рис 2.1) (колебание, изменяющееся по закону косинуса или синуса), описывается следующими выражениями:

(2.1)

где А₀, f₀, ₀, ₀ – постоянные величины, которые могут исполнять роль информационных параметров сигнала: А₀ – амплитуда, наибольшее отклонение какой-либо величины от положения равновесия или состояния покоя; f₀ – циклическая частота (имеет размерность в Гц); - угловая частота (имеет размерность рад/с); ₀ – начальная фаза или начальный угол отклонения. Период одного колебания .

Путем воздействия на тот или иной параметр несущего колебания (2.1) можно получить требуемый вид модуляции (манипуляции), т.е. воздействуя на амплитуду – мы получаем амплитудную модуляцию (АМ), на частоту – частотную (ЧМ), на фазу – соответственно фазовую (ФМ).

Если амплитуда и фаза сигнала изменяются существенно медленнее, чем несущая частота , то полоса спектра такого сигнала много меньше и сигнал называется узкополосным.

Если амплитуда и фаза меняются с частотой соизмеримой или большей, чем , то это широкополосный сигнал.

- Прямоугольные видеоимпульсы (рис.2.2,а)

(2.2)

- Прямоугольные радиоимпульсы (рис.2.2,б)

(2.3)

Рис.2.2

- Треугольные видео (или радио) импульсы (соответственно рис.2.2,а и рис.2.3,б)

Рис.2.3

- Последовательность отсчетов, тестовые сигналы и т.д.

2.2. Спектры детерминированных радиотехнических сигналов

Для детерминированных сигналов справедливы прямое и обратное преобразования Фурье

;	(2.4)
,	(2.5)

где - сигнал, а - его спектр. (Здесь - это не несущая частота, а гармонический ряд спектра сигнала).

Видеоимпульс. Ширина спектра видеоимпульса длительностью τ равна (рис 2.4,а), а база сигнала .

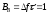Рис.2.4

Радиоимпульс. Ширина спектра радиоимпульса длительностью τ равна 2f (рис 2.4,б), а база такого сигнала .

Так как ширина спектра радиоимпульса в 2 раза больше, чем у видеоимпульса и база 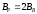, то амплитуды спектральных составляющих радиоимпульса в 2 раза меньше.

2.3. Корреляционный анализ детерминированных сигналов

Важной характеристикой детерминированных сигналов с ограниченной энергией является корреляционная функция (КФ)

,

(2.7)

где _τ - временной сдвиг копии сигнала .

Корреляция – математическая операция, схожа со свёрткой, позволяет получить из двух сигналов третий. Бывает: автокорреляция (автокорреляционная функция - характеризует степень связи между сигналом и его сдвинутой на длительность τ копией), взаимная корреляция (взаимнокорреляционная функция, кросскорреляционная функция - характеризует степень связи между 2-мя разными сигналами).

Корреляция - это техника обнаружения заранее известных сигналов на фоне шумов, ещё называют оптимальной фильтрацией.

Корреляционная функция для прямоугольного видеоимпульса. Сдвигая видеоимпульс 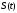(рис. 2.4,а) влево и вправо, и, вычисляя интеграл произведения исходного импульса на сдвинутый, получаем корреляционную функцию в пределах (рис 2.5,а). Энергия такого сигнала равна .

Свойства корреляционной функции:

1) При , , т.е. значение КФ равно полной энергии сигнала.

2) КФ – четная функция, т.е. .

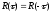3) , т.е. КФ имеет максимум при .

4) .

5) Функция R(τ) не несёт никакой информации о начальных фазах гармонических составляющих сигнала.

Корреляционная функция для радиоимпульса. Энергия радиоимпульса равна и в 2 раза меньше, чем энергия видеоимпульса. Корреляционная функция радиосигнала (рис.2.5,б) не зависит от начальной фазы радиоимпульса.

Рис.2.5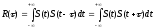