Аналитическая геометрия

_{Прямую линию на плоскости можно задать следующими уравнениями:}

_1.

_{Уравнение прямой, проходящей через точку (х0;у0 ) перпендикулярно вектору нормали .}

_2.

_{Каноническое уравнение прямой, т.е. уравнение прямой, проходящей через точку М0(х0;у0) параллельно направляющему вектору .}

_3.

_{Уравнение прямой, проходящей через две точки М1(х1;у1); М2(х2;у2).}

_4.

_{Уравнение прямой с угловым коэффициентом k, проходящим через точку М0(х0;у0).}

_{Пусть прямые заданы общими уравнениями:}

_{А1х+В1у+С1=0; А2х+В2у+С2=0}

_1.

_{Прямые имеют единственную точку пересечения. Для нахождения координат точки пересечения необходимо решить систему:}

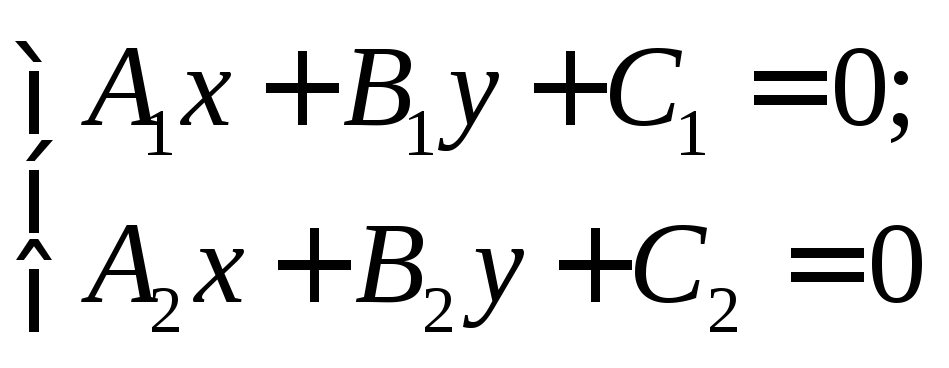
_{2. - прямые параллельны.}

_{3. - прямые совпадают.}

_{4.- прямые перпендикулярны.}

_{Уравнением поверхности в заданной системе координат называется уравнение с тремя переменными F(x,y,z)=0, которому удовлетворяют координаты точек, лежащих на ней.}

_{Пусть даны три точки в пространстве, не лежащие на одной прямой: М1(х1,у1,z1), M2(x2,y2,z2), M3(x3,y3,z3).}

_{Рассмотрим векторы:}

_{Тогда уравнение плоскости, проходящей через три точки ,будет иметь вид:}

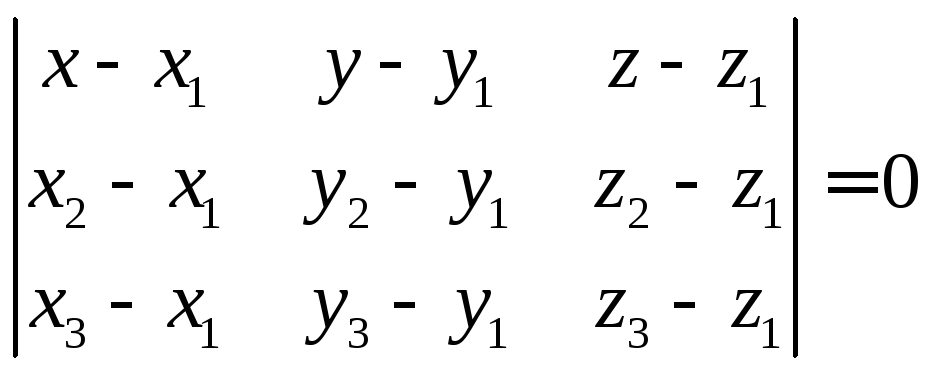
Уравнение плоскости, проходящей через точку с координатами (x₀;y₀;z₀) перпендикулярно вектору имеет вид:

Общее уравнение плоскости имеет вид

Пусть даны две плоскости

_{А1х+В1у+С1z+D1=0;}

_{А2х+В2у+С2z+D2=0}

_{Для того, чтобы плоскости были параллельны, необходимо и достаточно, чтобы их нормальные вектора были коллинеарны, т.е.}

_{Для того, чтобы плоскости были перпендикулярны, необходимо и достаточно, чтобы выполнялось условие:}

Если плоскости пересекаются, то угол между ними определяется соотношением:

Уравнения прямой в пространстве:

1.Каноническое уравнение прямой

2.Уравнение прямой, проходящей через две точки

Угол между прямой и плоскостью.

Пусть плоскость задана уравнением , вектор нормали которой, и задана прямая с направляющим вектором:

_Тогда

_{Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали и направляющий вектор были коллинеарны, т.е.}

_{Расстояние от точки до плоскости.}

Пусть плоскость задана уравнением и дана точкаМ₀(x₀;у₀;z₀),от которой нужно найти расстояние до плоскости. Тогда необходимо воспользоваться формулой:

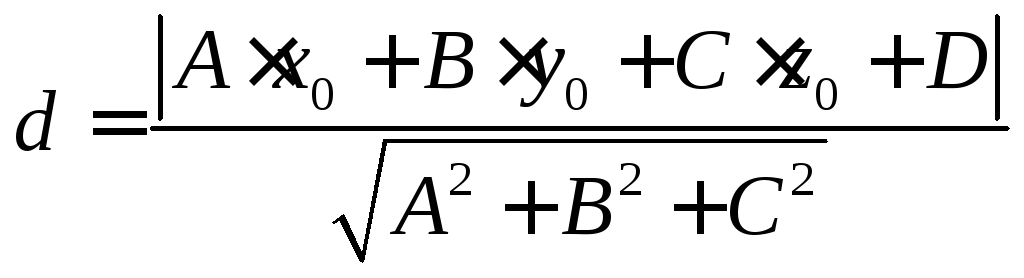
Примеры решения задач.

Задание 1. Проверить, лежат ли точки А(0;-2), В(10;-3), С(-9;10) на одной прямой.

Решение: проверим векторы на коллинеарность.

. Так как координаты не пропорциональны, то векторы не коллинеарны. Значит точки А, В, С не лежат на одной прямой.

Задание 2. Составить уравнение прямой АВ, если А(0;-2), В(10;-3).

Решение: прямая АВ задается точками А и В. Уравнение прямой имеет вид

_;

_{подставим координаты данных точек и упростим}

_{Задание 3.Составить уравнение высоты СК треугольника АВС, если А(0;-2), В(10;-3),С(-9;10).}

Решение: высота СК задается точкой С и нормальным вектором . Уравнение имеет вид :

тогда

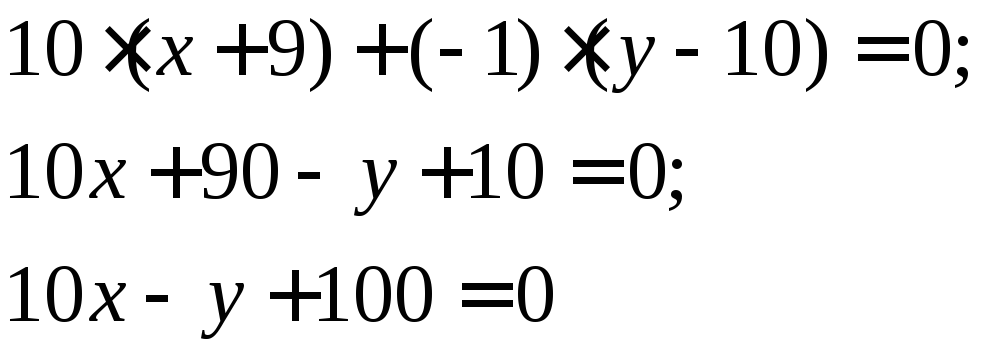
_{Задание 4.Составить уравнение медианы АД треугольника АВС, если А(0;-2), В(10;-3),С(-9;10).}

Решение: медиана АД задается точками А и Д. Д(0,5;3,5) – середина ВС.

_{Задание 5.Найти угол между медианой АД и стороной АС, если А(0;-2), В(10;-3),С(-9;10).}

_{Решение:}

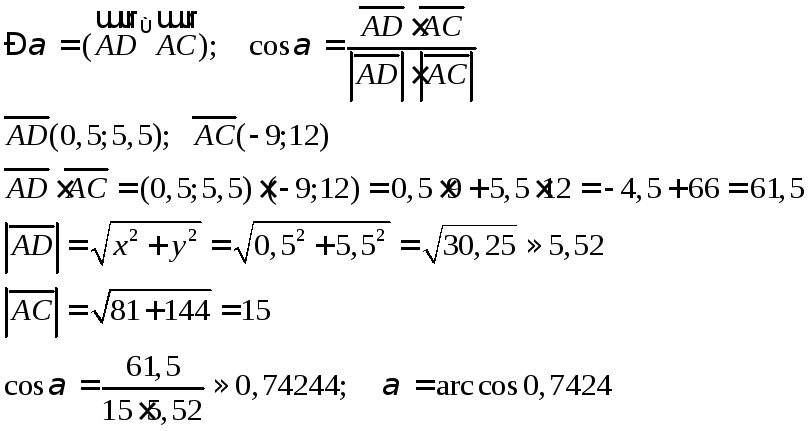
_{Задание 6.Найти площадь треугольника АВС, если А(0;-2), В(10;-3), С(-9;10).}

_{Решение:}

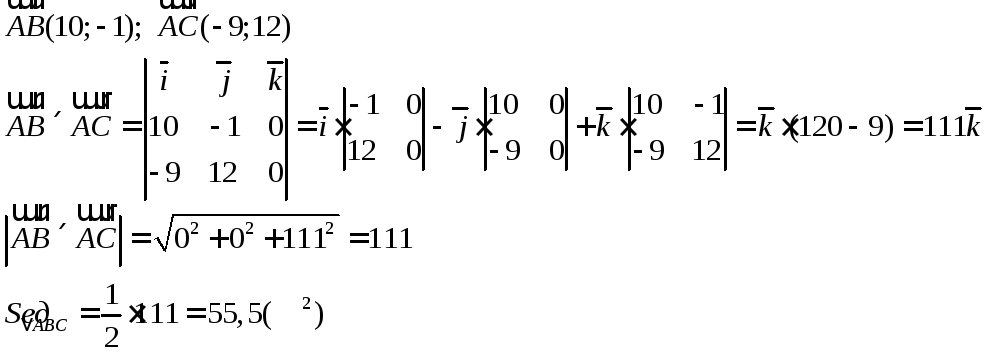
_{Задание 7. Проверить, лежат ли точки А(1;0;0), В(3;2;2), С(-1;0;1), Д(3;-5}¹_{/3;5) в одной плоскости.}

_{Решение:}

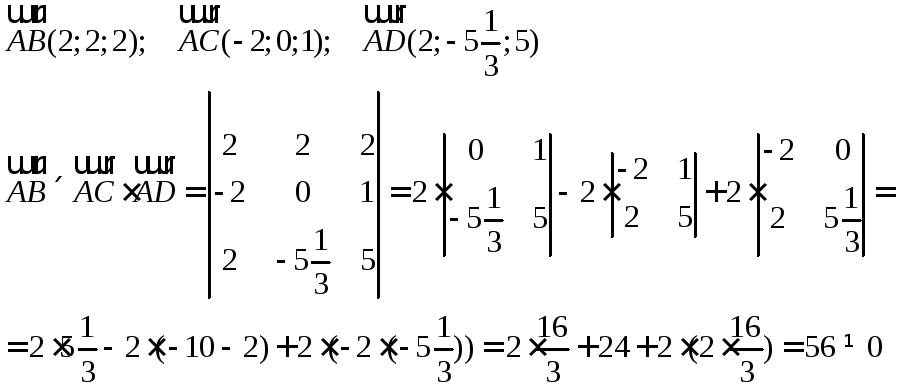
Задание 8. Составить уравнение прямой АВ, если А(1;0;0), В(3;2;2)

_{Решение:}

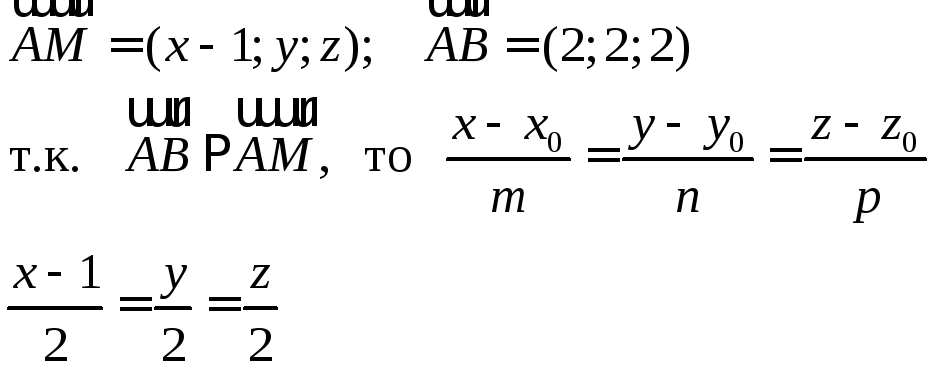
Задание 9. Составить уравнение плоскости АВС, если А(1;0;0), В(3;2;2), С(-1;0;1).

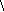
_{Решение:}

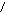
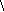
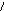
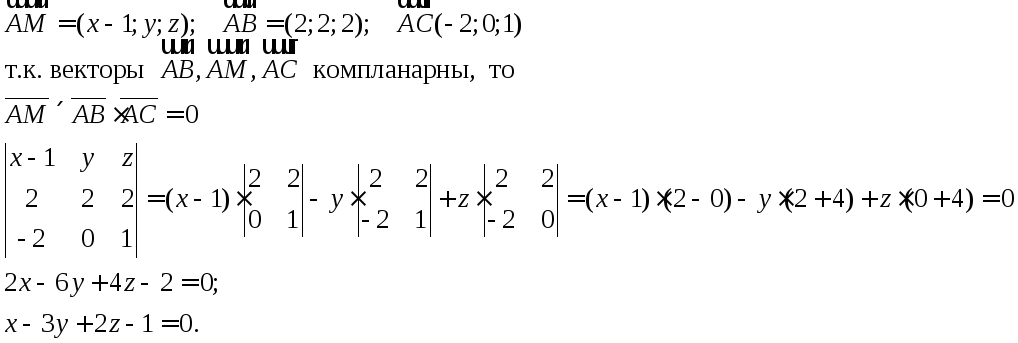
_{Задание 10.Найти площадь треугольника АВС, если А(1;0;0), В(3;2;2), С(-1;0;1).}

_{Решение:}

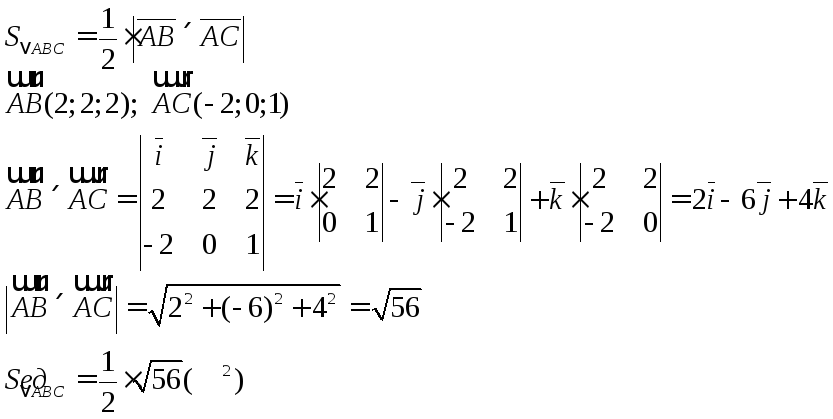
_{Задание 11. Составить уравнение высоты Н пирамиды АВСД, опущенной из вершины Д на основание АВС. Найти ее длину, если А(1;0;0), В(3;2;2), С(-1;0;1), Д(3;-5}¹_/3;5)

_{Решение:}

Уравнение плоскости АВС: Нормальный вектор плоскости АВС имеет координаты.

Уравнение высоты , где(x₀;y₀;z₀) – координаты т.Д, (l;m;n) – координаты нормального вектора.

Значит - уравнение ысоты.

Длина высоты вычисляется по формуле:

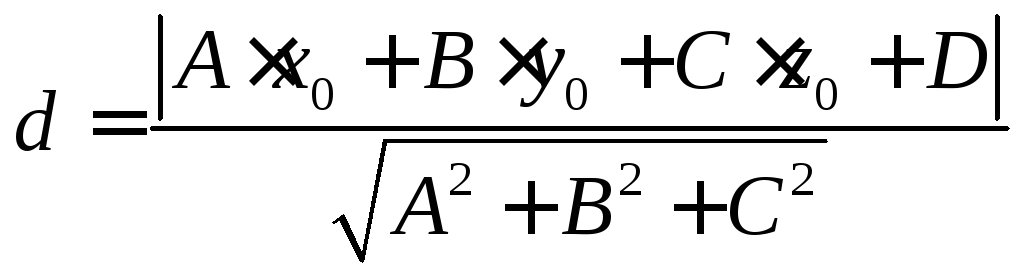
Тогда

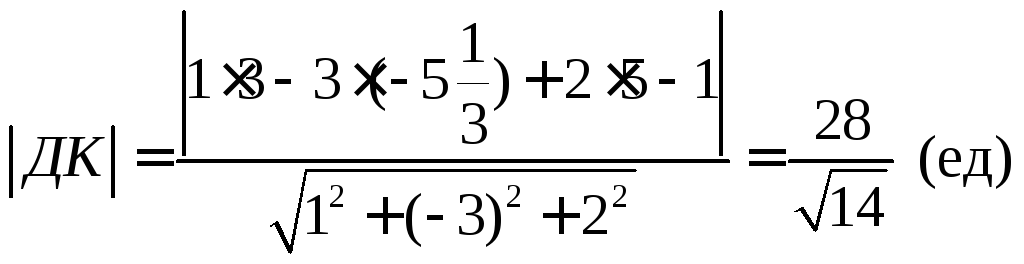
_{Задание 12. Найти координаты точки К – основания высоты (данные из задания 11).}

_{Решение:}

_{Решим систему}

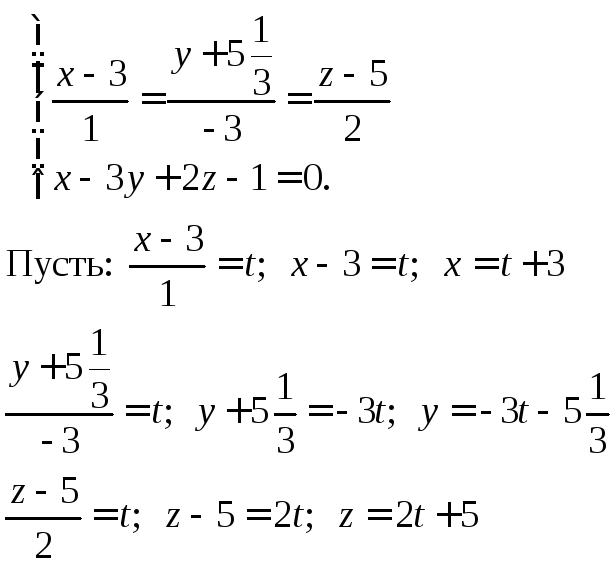
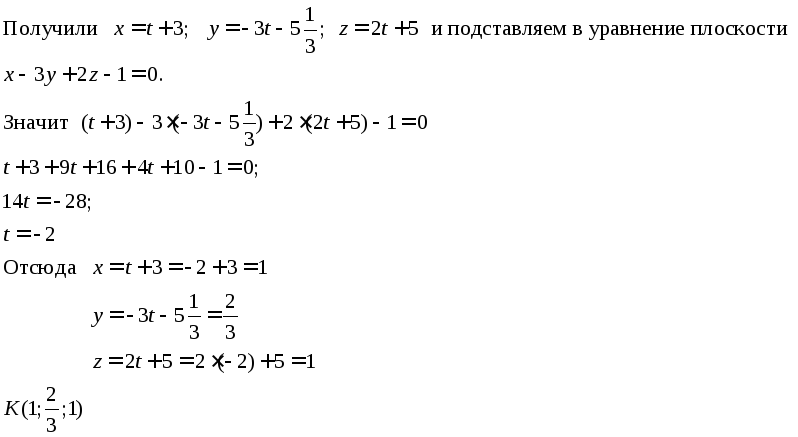
_{Задание 13. Найти угол между ребром ДА и основанием АВС, если А(1;0;0), В(3;2;2), С(-1;0;1), Д(3;-5}¹_/3;5).

_{Решение: воспользуемся формулой}

_{Задание 14. Найти угол между гранями АВС и АДС, если А(1;0;0), В(3;2;2), С(-1;0;1), Д(3;-5}¹_/3;5).

_{Решение: найдем уравнение плоскости АДС:}