Расчётно-графическая работа №1.

Задача 1. Найдите матрицу по известным матрицамА и В и проверьте равенство .

Задача 2. Найдите произведение матриц С и D .

Задача 3. Решите матричное уравнение и сделайте проверку решения.

Задача 4. Решите систему линейных уравнений по формуле Крамера и методом обратной матрицы.

Задача 5. Решите методом Гаусса систему линейных уравнений и сделайте проверку решения.

Векторная алгебра. Аналитическая геометрия.

1.Вектор. Виды векторов. Характеристики вектора.

2.Действия над векторами.

3.Координаты вектора. Действия над векторами в координатной форме.

4.Скалярное произведение векторов.

5.Векторное произведение векторов.

6.Смешанное произведение векторов.

7.Способы задания прямой на плоскости.

8.Уравнение плоскости и прямой на плоскости.

9.Уравнения прямой в пространстве.

10.Угол между прямой и плоскостью.

11.Расстояние от точки до плоскости.

Теоретический курс.

Вектор - упорядоченная пара точекА и В, где А называется началом вектора, а В – концом, т.е. вектор - это направленный отрезок, поскольку порядок на множестве концов создает определенное направление.

Расстояние между началом и концом вектора называется его длиной и обозначается .

Длина вектора вычисляется по формулам:

, где А(х₁;у₁) ; В(х₂;у₂)

или

, где а(х;у)

Векторы называются коллинеарными, если их линии действия параллельны.

Координатами вектора называются числа

х=х₂-х₁ и у=у₂-у₁ , если А(х₁;у₁) ; В(х₂;у₂)

Два вектора называются равными, если они коллинеарны, одинаково направлены и равны по длине.

Три вектора, расположенные в пространстве, называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

У коллинеарных векторов координаты пропорциональны.

Чтобы найти координаты середины отрезка (вектора), необходимо соответственные координаты сложить и разделить на два.

Например:

A(x₁;y₁) C(x;y) B(x₂;y₂)

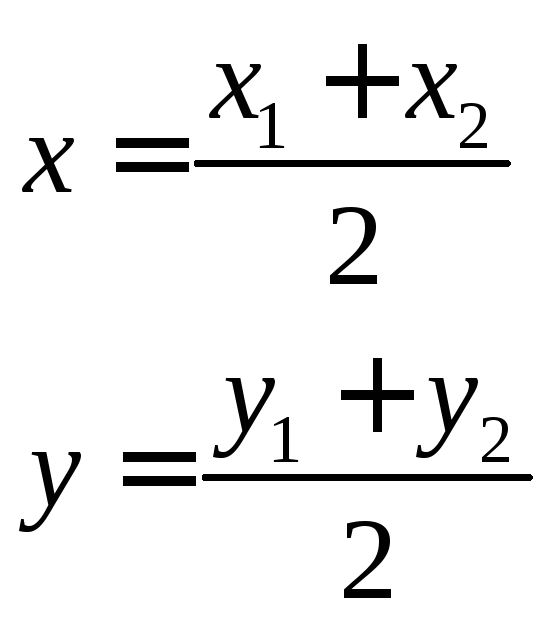
Суммой векторов иназывается вектор, соединяющий начало векторас концом векторапри условии, что начало векторасовпадает с концом вектора. Данное правило называется правилом треугольника.

Чтобы найти координаты суммы векторов, необходимо соответствующие координаты сложить :

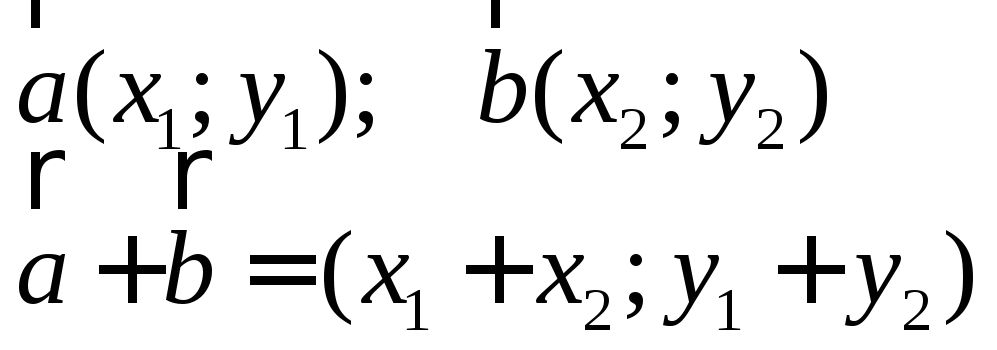
Произведением вектора на число n называется вектор, коллинеарный вектору и имеющий длину, равную, направление которого совпадает с направлением вектора, еслиn>0, и противоположно направлению вектора , еслиn<0.

Чтобы найти координаты вектора , умноженного на число, необходимо соответственные координаты умножить на это число:

Скалярным произведением векторов называется число, равное произведению длин этих векторов на косинус угла между ними:

Угол между векторами ивычисляется по формуле:

где

Скалярное произведение векторов, заданных своими координатами, равно сумме произведений соответственных координат

Векторным произведением вектора _{на вектор называется вектор, обозначаемый символом , для которого выполняются условия:}

1.Длина вектора _{равна площади параллелограмма, построенного на этих векторах, т.е.}

2.Вектор _{перпендикулярен плоскости векторов}

_{3. Упорядоченная тройка векторов - правая}

_{Пусть - векторы, заданные своими координатами в правом прямоугольном базисе , тогда разложение векторного произведения в том же базисе имеет вид:}

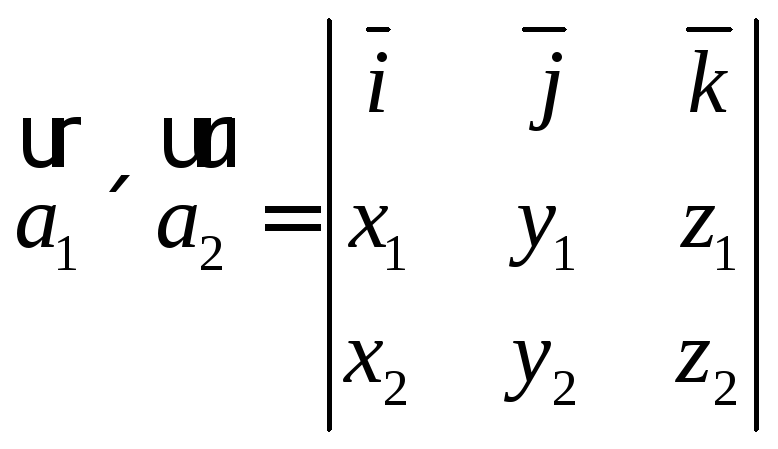
_{Пусть , тогда}

_{Смешанным произведением упорядоченной тройки векторов называется число (векторное произведение , скалярно умноженное на вектор ).}

_{Пусть в правом прямоугольном базисе заданы векторы. Смешанное произведение этих векторов вычисляется по формуле:}

_;

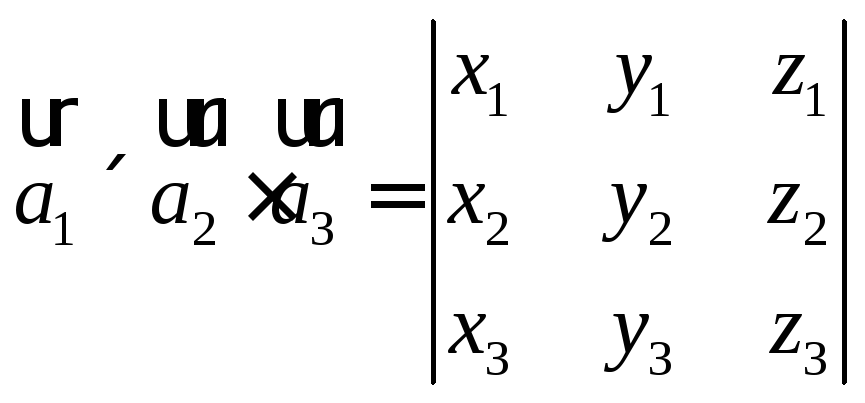_{т.е. смешанное произведение векторов равно определителю, составленному из координат данных векторов.}

_{Необходимым и достаточным условием компланарности трех ненулевых векторов является равенство нулю их смешанного произведения.}

_{С помощью смешанного произведения можно найти объем пирамиды. Необходимо знать координаты вершин пирамиды.}

_{Пусть , тогда находим координаты векторов и подставляем в формулу:}