Расчет цилиндрической оболочки

Меридиональный изгибающий момент

(3)

Нормальное кольцевое усилие

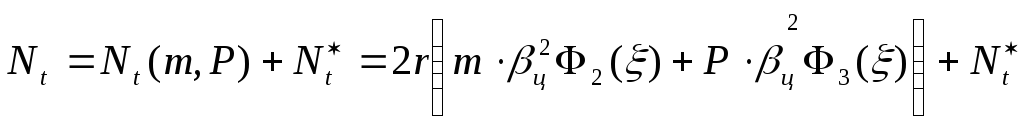, (4)

Радиальное перемещение

. (5)

Длина зоны краевого эффекта

380.988 мм.

Вычисления по формулам 3-5 выполняем для ряда значений аргумента () в интервале 0    3.2 c шагом .

Значения безмоментных составляющих нормального кольцевого усилия =1400.004 Н/мм и радиального перемещения заимствуем из решения задачи по безмоментной теории.

Результата расчета цилиндрической оболочки сводим в табл. 2.1.

Таблица 2.1.

Результаты расчета цилиндрической оболочки

	, Нмм/мм	, Н/мм	, Н/мм	Δ*, мм	Δ, мм
0	27004	1400.004	-3486	0,331	-1.437
0.4	9725.2	1400.004	-2911	0,331	-1.214
0.8	-124.7164	1400.004	-1727	0,331	-0.753
1.2	-4523.8	1400.004	-524.932	0,331	-0.286
1.6	-5530	1400.004	428.329	0,331	0.085
2	-4795.9	1400.004	1065	0,331	0.333
2.4	-3437.2	1400.004	1423	0,331	0.472
2.8	-2089.4	1400.004	1579	0,331	0.532
3.2	-1035.5	1400.004	1611	0,331	0.545

Расчет сферической оболочки

Меридиональный изгибающий момент

, (6)

Нормальное кольцевое усилие

, (7)

Радиальное перемещение

. (8)

Вычисления по формулам 6-8 проводим для ряда значений аргумента .

В интервале c шагом .

Значения безмоментных составляющих нормального кольцевого усилия = 1220,408 Н/мм и радиального перемещения заимствуем из решения задачи по безмоментной теории.

Координаты границы зоны краевого эффекта

=> ,

φ* = 0.601

S* = 705.9875мм;

Результата расчета сферической оболочки сводим в табл. 2.2.

Таблица 2.2.

Результаты расчета сферической оболочки

	, Нмм/мм	Н/мм	Н/мм	Δ*, мм	Δ, мм
0	27004	1220,408	-3535	0.314	-1.437
0,4	9535	1220,408	-2942	0.314	-1.219
0,8	-359.6432	1220,408	-1782	0.314	-0.791
1,2	-4728.4	1220,408	-617.042	0.314	-0.362
1,6	-5677.1	1220,408	300.629	0.314	-0.024
2,0	-4885.6	1220,408	910.275	0.314	0.2
2,4	-3481.8	1220,408	1251	0.314	0.326
2,8	-2104.2	1220,408	1397	0.314	0.38
3,2	-1033.8	1220,408	1425	0.314	0.39

По результатам расчета строим графики распределения меридиональных изгибающих моментов, нормальных кольцевых усилий и радиальных перемещений вдоль образующей сосуда в области сопряжения цилиндрической и сферической оболочек (рис. 2.3, 2.4, 2.5). На графиках видно, что изгиб оболочек локализован в узких зо­нах, примыкающих к крайним сечениям. За пределами этих зон напряженно-деформированное состояние оболочек практически не отличается от безмоментного состояния.

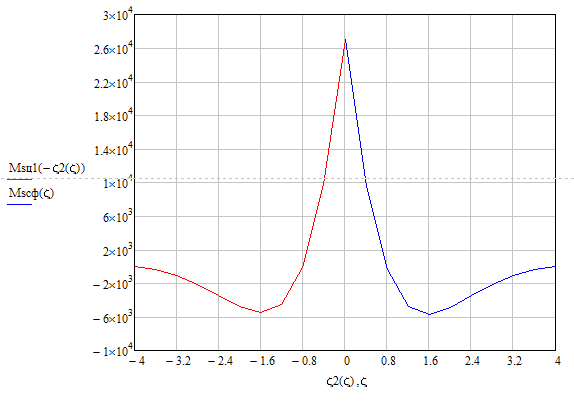
Рис. 2.8. Меридиональный изгибающий момент в зоне сопряжения

цилиндрической и конической оболочек

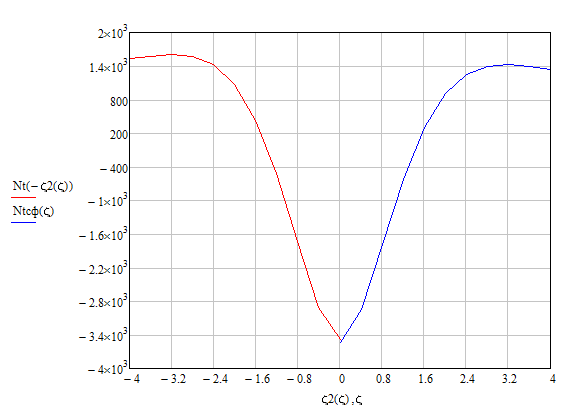
Рис. 2.9. Нормальное кольцевое усилие в зоне сопряжения

цилиндрической и конической оболочек

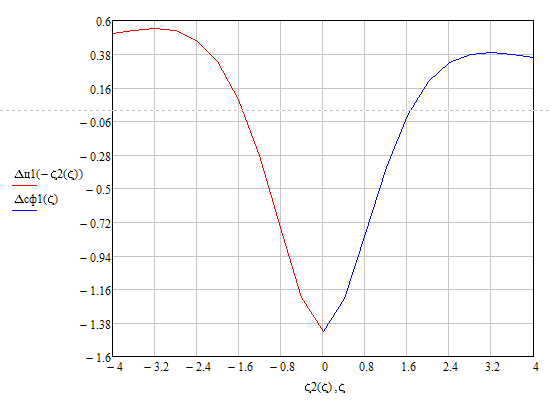
Рис. 2.10. Радиальные перемещения в зоне сопряжения цилиндрической и конической оболочек