Результаты расчета конической оболочки

	t* Н/мм2	s* Н/мм2	∆*·103 мм	ϑ*·104 рад
0	0	0	0	0
72.5	4.547	2.274	0.442	-0.406
145	9.095	4.547	1.768	-0.813
217.5	13.642	6.821	3.978	-1.219
290	18.19	9.095	7.072	-1.626
362.5	22.737	11.369	11.049	-2.032
435	27.285	13.642	15.911	-2.439
507.5	31.832	15.916	21.657	-2.845
580	36.38	18.19	28.287	-3.252
652.704	40.94	20.47	35.823	-3.659

Таким образом, в зонах краевого эффекта:

_t^*=40.94/мм²

_s^*=20.47/мм²

∆^*=35.823мм

ϑ^*=-3.659рад

2.1 Расчет узла сопряжения цилиндрической и сферической оболочки

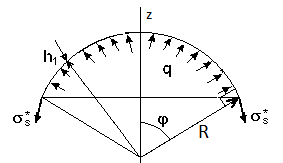
Для проверки результатов компьютерного расчета необходимо выполнить расчет узла сопряжения цилиндрической части оболочечной конструкции со сферической частью аналитическим методом. Схема представлена на рис. 2.1.

Д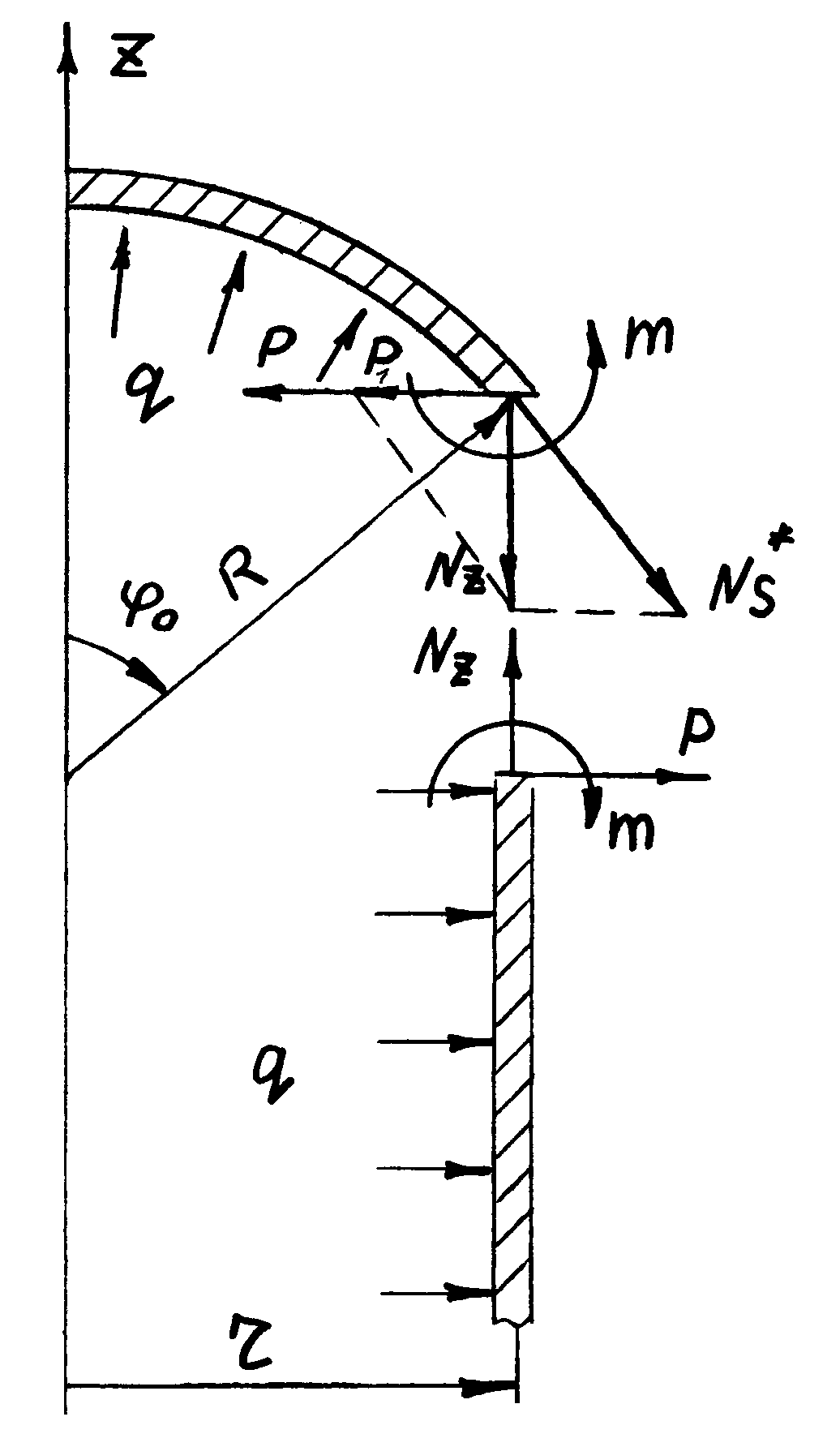ля решения узла сопряжения применяем метод сил. В соответствии с этим методом разрезаем (мысленно) оболочки и заменяем их действия друг на друга силами и моментами.

Определение неизвестных усилий

1) Составим уравнение равновесия сферической оболочки

в проекциях на ось z:

откуда находим

;Н/мм

2) По правилу параллелограмма разложим силу N_Z на N_S

и P₁:

;Н/мм

;Н/мм

Рис.2.1. Расчетная схема

3) Радиальное усилие P и момент m определяем из условия

совместной работы цилиндрической и сферической оболочек, полагая равными нулю относительные радиальное и угловое

перемещения их крайних сечений:

,

.

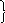Это означает, что радиальное перемещение крайнего сечения сферической оболочки и цилиндрического корпуса должны быть равны, и угол поворота крайнего сечения сферической оболочки должен быть равен углу поворота крайнего сечения цилиндрической оболочки, т.е.

,

.

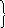
Воспользовавшись принципом независимости действия сил, из данных условий получаем следующие соотношения:

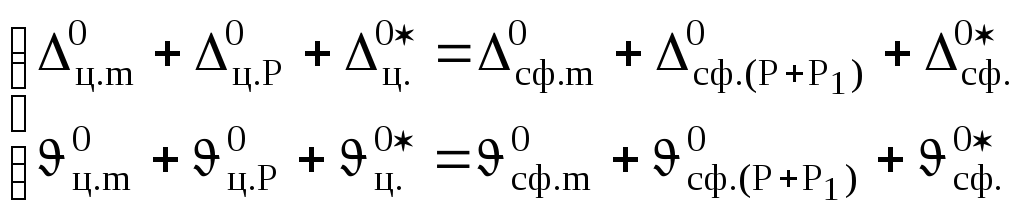, (1)

где индексами P, P₁ и m обозначены перемещения крайних сечений цилиндрической и сферической оболочек соответственно от кра­евых радиальных усилий и краевого момента, значком “” помече­ны перемещения от безмоментных составляющих нагрузки, т.е. отиq - для сферической оболочки; от N_Z и q - для цилиндри­ческой оболочки.

Для применения данной теории необходимо убедиться, что все рассматриваемые оболочки являются длинными. Для этого необходимо, чтобы их параметры удовлетворяли следующим условиям:

,

и для вершины конической оболочки

при.

Подставляя в систему (1) выражения для перемещений крайних сечений оболочек, получаем систему линейных алгебраических уравнений относительно неизвестных m и P:

,

(2)

,

Где

1.068 * 10⁸Нмм,

1.256*10⁸Нмм,

0.008 1/мм,

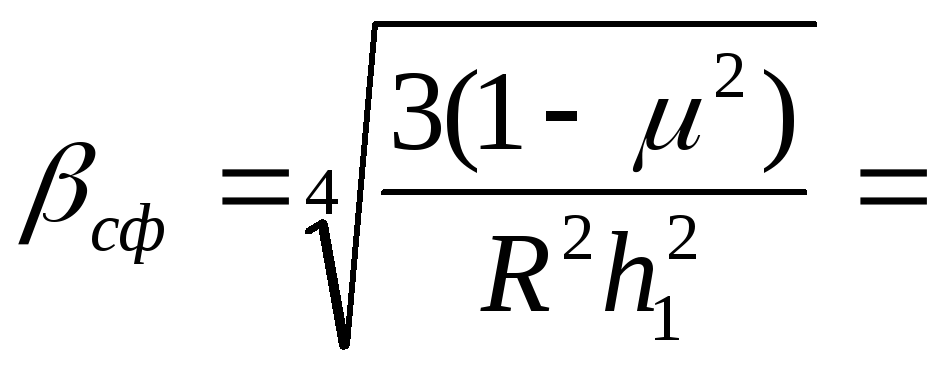0.006 1/мм.

Рис.2.2. Нахождение

По безмоментной теории найдем (рис.2.2):

МПа,

Т. к. для сферической оболочки , то из уравнения Лапласа

найдем

МПа,

тогда

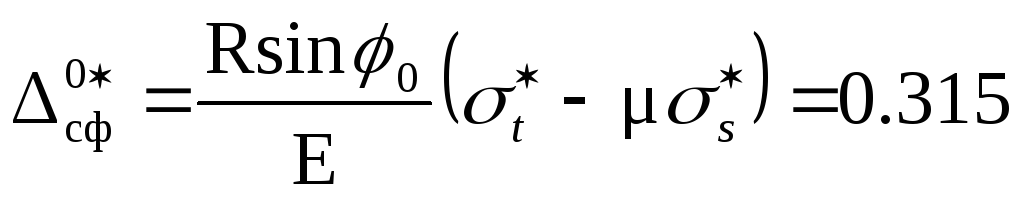мм

По безмоментной теории найдем :

Т.к. для цилиндрической оболочки

и , то из уравнения Лапласа

найдем

,

тогда

.

Т.к. q = const (увеличивается только r), то 0, аможно пренебречь из-за его малости.

Таким образом, у нас есть все необходимые данные, для решения системы (2). Решая эту систему линейных уравнений находим значения m и Р:

m = 27003.7262 Н·мм /мм,

P = -434.1536 Н/мм.

Определяем теперь внутренние усилия и перемещения в эле­ментах рассматриваемого узла.