График интенсивности напряжений

Рис.4

Выполним оценку прочности оптимизированной конструкции аппарата.

Рассмотрев график интенсивности напряжений (Рис.4), можно выделить несколько зон с наибольшими значениями интенсивности напряжений. Поиск наиболее опасной точки осложняется тем, что элементов на этот раз 6, т.е. количество сечений, которые следует рассмотреть, становится больше. Элементы №2 и №5 просматриваем полностью, т.к. по графику они представляют наибольший всплеск интенсивности напряжений.

По таблицам 4.14-4.19 , найдём наибольшее значение интенсивности напряжений на внутренней и внешней сторонах оболочки в каждом элеме

Таблица 4.20.

Точки с наибольшим напряжением	№ точки оболочного элемента	, МПа	, МПа
Конус	85	77.1	84.1
Тор ( стык конус-цилиндр)	42	145.5	72.9
Цилиндр (стык конус-цилиндр)	28	70.4	72.8
Цилиндр (стык сфера-цилиндр)	100	154	70.9
Тор ( стык сфера-цилиндр)	13	83.9	26.1
Сфера	70	94.1	90.3

Наибольшее значение интенсивности напряжений находится в элементе Цилиндр конус-цилиндр (Элемент №3) в сечении № 100 на внутренней стороне оболочки интенсивность напряжений достигает

По полученным результатам, видно, что напряжения в результате оптимизации удалось существенно приблизить к безмоментному состоянию:

= 1,7

К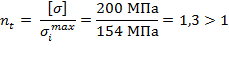оэффициент запаса прочности по пределу текучести:

5. Сравнительный анализ напряженно-деформированного состояния исходной и оптимизированной конструкции аппарата

Проведём сравнительный анализ конструкции до оптимизации и после:

В первую очередь следует сравнить максимальные значения интенсивности напряжений и их отношение к безмоментной составляющей.

До оптимизации = 862.1 Мпа, после оптимизации = 154 Мпа.

Отношение до оптимизации бло равно 8, после оптимизации - 1,7.

Теперь сравним коэффициенты запаса прочности по пределу текучести:

До оптимизации 0,23. После оптимизации 1,3

Полученные результаты для наглядности сведём в таблицу

Таблица 5.1.

	До оптимизации	После оптимизации
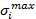
	862,1 МПа	154 МПа
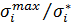
	8	1.7
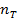
	0.23	1.3

Исходя из таблицы 5.1 можно сделать ввод, что оптимизация проведена успешно: запаса прочности хватает, а значит конструкция выдерживает заданную нагрузку.

Нам удалось снизить максимальную интенсивность напряжений в:

100