
- •Введение
- •8.1 Первообразная. Табличные интегралы
- •8.2 Методы интегрирования
- •8.3 Интегрирование рациональных дробей
- •8.4 Метод Остроградского
- •8.5 Интегрирование некоторых других выражений
- •9.1 Определение интеграла Римана
- •9.2 Условия интегрируемости. Суммы Дарбу
- •9.3 Линейные свойства определённого интеграла
- •9.4 Интегрируемость сложной функции
- •9.6 Связь определённого и неопределённого интегралов
- •9.7 Теоремы о среднем
- •9.8 Некоторые классические неравенства для интегралов
- •9.9 Приближённое вычисление интегралов
- •9.10 Несобственные интегралы
- •9.11 Задачи и упражнения
- •Глава 10 Интеграл Римана–Стилтьеса
- •10.1 Функции ограниченной вариации
- •10.2 Определение интеграла Римана–Стилтьеса
- •10.3 Свойства интеграла Римана–Стилтьеса
- •10.4 Задачи и упражнения
- •Глава 11 Функции многих переменных
- •11.1 Многомерные евклидовы пространства
- •11.2 Открытые и замкнутые множества
- •11.3 Пределы функций многих переменных
- •11.4 Непрерывные функции многих переменных
- •11.5 Задачи и упражнения
- •Глава 12 Дифференциальное исчисление функций многих переменных
- •12.2 Касательная плоскость
- •12.3 Дифференцируемость сложной функции
- •12.4 Производная по направлению. Градиент
- •12.5 Частные производные и дифференциалы высших порядков
- •12.6 Формула Тейлора
- •Глава 13 Неявные функции
- •13.1 Свойства функций, заданных неявно
- •13.2 Система неявных функций
- •Глава 14 Экстремумы функций многих переменных
- •14.1 Локальные экстремумы
- •14.2 Условный локальный экстремум
- •14.3 Метод неопределённых множителей Лагранжа
- •Краткие сведения об ученых, упоминаемых в тексте

Глава 13. Неявные функции
§ 13.1. Свойства функций, заданных неявно
До сих пор изучались функции вида = (x), когда каждой точке из области задания функции каким-либо способом (например, с помощью формулы) ставилось в соответствие число – значение функции. В таких случаях функции считают заданными явно.
О неявном задании функций, короче о неявных функциях, говорят, когда переменные x и связаны равенством (x, ) = 0 и считается функцией от x, т.е. когда уравнение (x, ) = 0 нужно решить относительно . Понятно, что это не всегда возможно.
Поясним на простом примере постановку вопроса и характер ожидаемых результатов.
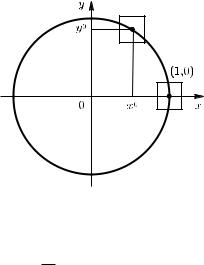
Пусть числа и связаны уравнением единичной окружности
2 + 2 − 1 = 0. |
(13.1.1) |
Точкам [−1, 1] в силу (13.1.1) соответствуют значения
√
= ± 1 − 2. Так как знак + или − в каждой точке можно выбрать произвольно, уравнение (13.1.1) зада¨ет бесконечно много функций.
Если же рассматривать только непрерывные функции, то уравнение (13.1.1) определяет на [−1, 1] две функции
√
= 1 − 2 (13.1.2)
и
√
= − 1 − 2.
Графиком первой из них является верхняя полуокружность, а графиком второй – нижняя полуокружность. Таким образом, уравнение (13.1.1) не определяет на отрезке [−1, 1] непрерывную функцию однозначно.
Перейд¨ем от такой глобальной постановки вопроса к локальной и рассмотрим вопрос о разрешимости уравнения (13.1.1) не
166
§ 13.1. Свойства функций, заданных неявно |
167 |
во всей полосе | | 6 1, а только в окрестности некоторой точки ( 0, 0) окружности (13.1.1). Пусть для определ¨еннсти эта точка лежит на верхней полуокружности.
Если | 0| < 1, то в достаточно малой окрестности точки ( 0, 0) уравнение (13.1.1) зада¨ет функцию формулой (13.1.2). Графиком этой функции является часть окружности, содержащаяся в рассматриваемой окрестности.
А если в качестве ( 0, 0) взять точку (1, 0), то ни в какой окрестности этой точки уравнение (13.1.1) не зада¨ет однозначную непрерывную функцию.
Заметим, что частная производная по функции из левой части уравнения (13.1.1)
∂∂ ( 2 + 2 − 1) = 2
в точках ( 0, 0) при | 0| < 1 не равна нулю, а в точке (1, 0) эта производная обращается в нуль.
Отмеченные свойства функции (13.1.2), определяемой уравнением (13.1.1), характерны при неявном задании функций и в общем случае.
Будем рассматривать вопрос об как функции переменных1, . . . , , заданной неявно уравнением
( 1, . . . , , ) = 0. |
(13.1.3) |
Множество точек ( 1, . . . , , ) пространства E +1, координаты которых удовлетворяют уравнению (13.1.3), обозначим .

168 Гл. 13. Неявные функции
Выясним, при каких условиях в некоторой окрестности точки
( 0, . . . , 0 , 0) множества существует непрерывная функция
1
= ( 1, . . . , ), графиком которой являются все точки , содержащиеся в этой окрестности. Иначе говоря, в некоторой -
мерной окрестности точки ( 0 |
, . . . , 0 |
) тождественно выполняет- |
1 |
|
|
ся равенство |
|
|
( 1, . . . , , ( 1, . . . , )) = 0.
|
Теорема 13.1.1. Пусть в некоторой шаровой окрестности |
|
E +1 точки ( 10, . . . , 0 , 0) задана непрерывная функция |
( 1, . . . , , ), которая в этой точке обращается в нуль и для |
|
каждой точки ( *, . . . , * ) проекции шара на плоскость = 0
1
функция ( *, . . . , * , ) переменной строго возрастает.
1
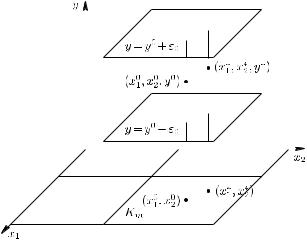
Тогда для каждого положительного числа существуют такие положительные числа 0 и , что 0 < и решением уравнения (13.1.3) относительно в ( + 1)-мерном прямоугольнике
+1 := {( 1, . . . , , ) : | − 0| 6 , = 1, . . . , ; | − 0| < 0}
является функция = ( 1, . . . , ), непрерывная в -мерном кубе
|
|
:= {( 1, . . . , ) : | − 0| 6 , = 1, . . . , }, |
|
|
||||||
т.е. в точках ( 1, . . . , ) этого куба справедливо равенство |
|
|||||||||
|
|
( 1, . . . , , ( 1, . . . , )) = 0. |
|
|
(13.1.4) |
|||||
Доказательство. По заданному выбираем положительное |
||||||||||
число |
0 |
< так, чтобы обе точки ( 0, . . . , 0 , 0 |
+ |
0 |
) и ( 0 |
, . . . , 0 |
, |
|||
|
|
0. |
1 |
|
|
1 |
|
|||
0 − 0) лежали в шаре |
0 |
|
|
|
при |
= |
0 |
|||
Так как функция ( |
1 |
, . . . , , ) переменной |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
обращается в нуль и на отрезке, соединяющем точки ( 0, . . . , 0 |
, |
|||||||||
|
|
|
|
|
|
|
|
1 |
|
|
0 − 0) и ( 10, . . . , 0 , 0 + 0), строго возрастает, то |
|
|
||||||||
|
|
( 0, . . . , 0 , 0 + 0) > 0 |
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
и |
|
( 10, . . . , 0 , 0 − 0) < 0. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||
Поскольку функция ( 1, . . . , , ) |
в окрестности непре- |
|||||||||
рывна, существует такое положительное число , что для всех
§ 13.1. Свойства функций, заданных неявно |
169 |
точек ( 1, . . . , , 0 + 0), принадлежащих пересечению гиперплоскости = 0 + 0 пространства E +1 с , первые коорди-
нат которых удовлетворяют условиям | − 0| < , = 1, . . . , ,
выполняется неравенство
( 1, . . . , , 0 + 0) > 0
идля всех точек ( 1, . . . , , 0 − 0), принадлежащих пересече-
нию гиперплоскости = 0 − 0 с , при тех же условиях на ,= 1, . . . , , выполняется неравенство
( 1, . . . , , 0 − 0) < 0.
Таким образом получен ( +1)-мерный прямоугольник +1, лежащий в окрестности . Покажем, что в этом прямоугольнике выполняются утверждения теоремы.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим |
произвольную точку ( *, . . . , * |
), принадле- |
|||||||||||||||||||
жащую кубу |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||
|
. На отрезке, соединяющем точки ( *, . . . , * , |
|||||||||||||||||||||
0 |
|
|
|
) |
|
|
|
, 0 |
+ |
|
) |
|
|
|
|
|
1 |
|
|
|||
− |
0 |
и |
( *, . . . , * |
0 |
, первая из которых |
принадлежит |
||||||||||||||||
|
|
|
1 |
|
0 |
|
|
|
|
|
0 |
+ 0, |
||||||||||
гиперплоскости = |
|
− 0, а вторая – гиперплоскости = |
|
|||||||||||||||||||
функция ( *, . . . , * |
, ) строго возрастает, прич¨ем в нижнем кон- |
|||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
це этого отрезка она отрицательна, а в верхнем положительна. Значит, существует единственное значение переменной , при ко-
тором функция ( *, . . . , * , ) равна нулю.
1

170 |
|
Гл. 13. Неявные функции |
Обозначим это значение * и положим |
||
( * |
, . . . , * |
) := *. |
1 |
|
|
Итак, в кубе определена функция ( 1, . . . , ), для которой выполняется равенство (13.1.4). Докажем непрерывность
функции . |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Заметим сначала, что по построению функция ( 1, . . . , ) |
||||||||||||||
непрерывна в точке ( 0, . . . , 0 |
|
). В самом деле, для произволь- |
||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
ного 0 > 0 было найдено |
> 0 такое, что во всех точках куба |
|||||||||||||||
|
|
значения функции ( |
|
, . . . , |
) заключены между 0 |
− |
|
|
и |
|||||||
|
0 |
|
|
, т.е. отличаются от |
1 |
|
0 |
|
|
0 |
|
|
0 |
|
||
|
+ |
0 |
( |
1 |
, . . . , ) меньше, чем на |
0 |
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Но в качестве исходной точки в проведенных рассуждениях |
||||||||||||||
можно было взять любую из построенных точек ( *, . . . , * |
, *) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
прямоугольника +1. Поэтому функция ( 1, . . . , ) непрерывна во всех точках куба .
Теорема доказана.
Понятно, что в этой теореме строгое возрастание функции
( *, . . . , * , ) можно заменить на строгое убывание.
1
Покажем, что функция ( 1, . . . , ) из теоремы 13.1.1 при некоторых дополнительных условиях имеет частные производные.
Теорема 13.1.2. Пусть функция ( 1, . . . , , ) удовлетворяет условиям теоремы 13.1.1. Если частные производные пои по некоторой переменной непрерывны на множестве и
∂ ( 0, . . . , 0 , 0) ̸= 0, ∂ 1
то функция ( 1, . . . , ), являющаяся решением уравнения (13.1.3), в достаточно малой окрестности каждой точки xимеет непрерывную частную производную ∂ /∂ , для которой справедливо равенство
|
∂ |
(x) = − |
∂ |
(x, (x)) |
∂ |
(x, (x)). |
(13.1.5) |
|
|
∂ |
∂ |
∂ |
|||||
Доказательство. Для |
упрощения записи будем |
считать |
||||||
( 1, . . . , , ) функцией только переменных и , так как все остальные аргументы в проводимых рассуждениях будут оставаться фиксированными. Тогда функция зависит только от .

§ 13.1. Свойства функций, заданных неявно |
171 |
Вслучае, когда является функцией только переменных
и, куб представляет собой отрезок.
Будем придавать переменной приращения , при которых точки + принадлежали .
Если := ( ) и := ( + ) − ( ), то согласно определению функции имеем
( , ) = 0
и
( + , + ) = 0.
Значит,
( + , + ) − ( , ) = 0.
Применив к этой разности формулу конечных приращений для функций многих переменных (12.6.3), находим, что при некотором 0 < < 1
( + , + ) − ( , ) =
∂
=∂ ( + , + ) +
+ |
∂ |
( + , + ) = 0. |
(13.1.6) |
|
∂ |
||||
|
|
|
Но → 0 при → 0 в силу непрерывности функции ( ). Так как частная производная функции по в рассматриваемой окрестности отлична от нуля и непрерывна, то из равенства
(13.1.6) следует, что
|
|
= − |
∂ |
( + , + ) |
|
∂ |
( + , + ), |
|
|
∂ |
∂ |
(13.1.7) прич¨ем в правой части (13.1.7) можно перейти к пределу при→ 0 отдельно в числителе и в знаменателе.
Таким образом,
→0 |
|
= − |
∂ |
( , ) |
|
∂ |
( , ). |
|
∂ |
∂ |
|||||
lim |
|
|
|
|
|
|
|
Это показывает существование производной ∂ /∂ , е¨ непрерывность и справедливость равенства (13.1.5).
Теорема доказана.

172 |
Гл. 13. Неявные функции |
Формула (13.1.5) позволяет указать условия на функцию , достаточные для существования частных производных функциивторого и более высокого порядка.
Так, согласно теореме 12.3.1 о производных сложной функции из (13.1.5) следует, что функция (x) имеет непрерывную чистую частную производную второго порядка по переменной , если непрерывны частные производные
∂2 |
|
∂2 |
∂2 |
|||
|
, |
|
, |
|
|
. |
2 |
|
∂ |
2 |
|||
∂ |
|
∂ ∂ |
|
|
||
|
|
|
|
|
|
|
А если функция имеет непрерывные частные производные второго порядка
∂2 |
, |
∂2 |
, |
∂2 |
, |
∂2 |
∂ ∂ |
∂ ∂ |
∂ ∂ |
∂2 |
при ̸= , то имеет непрерывную смешанную частную производную
∂2
∂ ∂
.
Проиллюстрируем применение полученных результатов на задаче об обратной функции одной переменной.
Рассмотрим функцию = ( ). Если значения независимой переменной обратной функции обозначать , а значения зависимой переменной , то нужно решить относительно уравнение
= ( ).
Запишем это уравнение в виде
− ( ) = 0. |
(13.1.8) |
Согласно теоремам 13.1.1 и 13.1.2, если функция ( ) и е¨ производная / непрерывны в некоторой окрестности точки 0,0 := ( 0) и ′( 0) ̸= 0, то существует окрестность точки ( 0, 0), в которой уравнение (13.1.8) можно разрешить относительно , т.е. это уравнение равносильно равенству = ( ), где ( ) – непрерывная функция.
Так как функция из левой части уравнения (13.1.8) имеет непрерывную производную по , то функция ( ) имеет непрерывную производную и согласно (13.1.5)
′( 0) = − |
1 |
= |
1 |
. |
− ′( ( 0)) |
′( 0) |
