
Чистяков Ч1
.pdf
Рис. 42. К расчёту тока электронов на плоский зонд для общего случая.
91

Полный ток электронов на зонд
|
|
|
|
|
|
e |
2π r |
|
|
φм |
∞ |
|
|
|
|
|
|
|
|
|
|
|||||
|
Iз = |
|
∫ ∫∫ |
∫ |
∫ |
f (v)sinφcosφdvdψdrdφdσ |
|
(80) |
||||||||||||||||||
|
4π |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
0 0 σ 0 v |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мин |
|
|
|
|
|
|
|
|
|
|
|
Интегрируем выражение (80) по |
ψ , σ |
и |
r |
(на единицу времени): |
|
|||||||||||||||||||||
|
|
|
|
|
|
eσ |
ϕм |
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
I |
з |
= |
2 |
∫ |
|
∫ |
f |
(v)vsinϕcosϕdϕdv . |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 v |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
мин |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
2eu |
|
|
|
|
|
|
|
|
|
|
|||||||||
Имея в виду, что |
cos2 ϕ |
|
|
|
= |
|
|
и |
v |
|
|
= 2 |
e |
u , получаем определенный |
||||||||||||
макс |
mv2 |
мин |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|||||||||||||
интеграл, зависящий от параметра |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
eσ |
|
|
∞ |
|
|
|
|
|
|
|
|
2eu |
|
|
|
|
|
|
|
||
|
I |
|
|
= |
|
|
|
|
∫ |
|
|
|
|
f (v)v(1− |
|
|
)dv . |
|
|
(81) |
||||||
|
з |
4 |
|
|
|
|
|
|
mv2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2 |
e |
u |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для того чтобы |
выразить |
функцию |
распределения |
f (v) |
через |
ток и |
||||||||||||||||||||
напряжение на зонде, следует произвести дифференцирование под знаком интеграла, зависящего от параметра*
[*формула для дифференцирования:
dI |
з |
|
eσ |
|
∞ |
2e |
||
|
= − |
|
|
∫ |
|
|||
du |
4 |
|
m |
|||||
|
2 |
e |
u |
|||||
|
|
|
|
|
||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
m |
|
|
откуда
|
|
|
|
d |
|
x2 |
|
|
|
|
|
|
|
|
|
x2 |
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
2 |
|
||||||||
|
|
|
|
|
|
|
∫ |
f (x, y)dx = |
∫ |
|
|
|
|
|
|
f |
(x, y)dy + f (x y) |
|
− f (x y) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
2 |
|
dy |
1 |
|||||||||||||
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (v) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2eu |
|
dv |
мин |
|
|
e2σ |
|
∞ |
|||||||||||||
|
|
|
|
dv |
− f (vмин)vмин(1 |
− |
|
|
|
|
|
|
|
|
|
) |
|
|
|
= − |
|
|
|
∫ f (v)v |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
2мин |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mv |
|
|
du |
|
|
|
2m vмин |
|||||||||||||
|
d |
2I |
з |
= |
|
e2σ f (v |
мин |
) dv |
мин |
= |
|
e2σ |
(v |
|
|
) , |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
мин |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
du2 |
|
|
2m vмин |
|
|
|
du |
|
|
|
|
|
|
4mu |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
) = 4 |
m |
|
u |
|
d2Iз |
. |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
f ( 2 |
e |
u |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
e eσ du2 |
|
|
|
|
|
|
|
|
|||||||||||||
dx1 )] dy
−1dv ,
(82)
2
Таким образом, по величине d 2Iз при определенном значении потенциала d u
зонда относительно плазмы u можно вычислить функцию распределения для
соответствующей величины скорости частиц v = 
 2 e u . Производя различные m
2 e u . Производя различные m
92

вычисления при различных значениях u , можно построить всю функцию f (v) .
Этот результат приложим к зондам различной формы – плоским, сферическим и
цилиндрическим. На рис. 43 графически определены |
dIз |
; |
d2Iз |
, а также функция |
|
|
|||
|
du |
du2 |
||
f (v) u d2I2з . du
Экспериментальный метод нахождения функции распределения электронов в плазме используется сейчас весьма широко. Сконструированы специальные приборы для быстрого автоматического определения этой функции.
13. Законы подобия
Значение законов подобия электрических разрядов в газах заключается не столько в формулировке новых истин, сколько в том, что они дают возможность эффективно и просто представить имеющуюся информацию о параметрах разрядов при различных условиях.
Законы подобия требуют геометрического и физического подобия.
Условие геометрического подобия разрядных пространств или промежутков (рис. 44) можно выразить следующим образом:
D1 |
= |
L1 |
= |
d1 |
= |
x1 |
= |
λ1 |
= a , |
(83) |
|
D2 |
L2 |
d2 |
x2 |
λ2 |
|||||||
|
|
|
|
|
|
где x - любой соответствующий размер; a - геометрический коэффициент подобия. Условие физического подобия состоит в следующем. В соответствующих
элементарных объемах разрядников должны протекать одни и те же элементарные процессы и с одинаковой интенсивностью, что обеспечивается одинаковыми функциями распределения электронов по скоростям, а при максвелловском распределении равенством температур Te1 = Te2 .
Если в разряде играют роль положительные ионы, то для них формулируется аналогичное условие. Кроме этих условий необходимо, чтобы разрядники были наполнены одним и тем же газом и электроды изготовлены из одного и того же материала. Если все эти условия выполнены, то согласно закону подобия два подобных разрядных промежутка при одинаковых напряжениях на электродах проводят одинаковый ток.
93

Рис.43. Графическое определение функции распределения электронов по скоростям в газе согласно формуле (82).
Рис. 44. Подобные разрядные приборы.
94

Рассмотрим как преобразуются различные величины при переходе от одного разрядного пространства к другому:
1) давление газа
p1 = λ2 = 1 ; p2 λ1 a
2) напряженность поля при равенстве напряжений на разрядниках U1 = U2
E1 = U1 d2 = 1 ;
E2 d1 U2 a
3) плотность зарядов, исходя из уравнения Пуассона divE = − ρ ,
ε0
|
|
ρ1 |
= |
E1 |
|
|
|
|
x2 |
= |
1 |
|
; |
|
|
||||||||
|
|
|
|
|
|
|
|
|
a2 |
||||||||||||||
|
|
ρ2 |
E2 |
|
x1 |
|
|
|
|
|
|
|
|
||||||||||
|
4) плотность тока |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
j = ρu , u = u |
|
|
j1 |
= |
|
ρ1u1 |
= |
1 |
; |
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
1 |
2 |
|
|
j2 |
|
|
|
ρ2u2 |
|
|
a2 |
|||||||||||
|
5) время перемещения частиц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
τ1 |
= x1 : |
|
|
x2 |
= a . |
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
τ2 |
u1 |
|
|
|
|
u2 |
|
|
|
|
|
|
|
|
||||||
|
Анализ всех элементарных процессов с точки зрения справедливости законов |
||||||||||||||||||||||
подобия может быть произведен с помощью уравнения непрерывности |
|||||||||||||||||||||||
|
|
|
∂ρi |
= −divj |
+ |
|
i |
, |
|
|
|
|
|
||||||||||
|
|
|
∂t |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
i - объемный коэффициент, характеризующий возникновение и разрушение |
||||||||||||||||||||||
частиц i - го вида. Для соответствующих элементарных объемов разрядных пространств уравнения непрерывности должны быть одинаковы, так как описывают одинаковые процессы, протекающие с одинаковой интенсивностью.
Для второго разрядного пространства (или разрядника) величины, входящие в уравнение непрерывности в случае выполнения законов подобия, могут отличаться только постоянным множителем:
A |
∂ρi = A |
i |
− A divj . |
|
∂t |
i |
|
|
|
|
Исследуем отдельные члены этого уравнения при переходе ко второму разрядному объему
∂ρ∂t 1
|
∂ρ |
|
Δρ |
t |
2 |
|
1 |
|
|
|
|
= |
1 |
|
= |
|
, |
||
t1 |
a3 |
||||||||
|
∂t 2 |
|
Δρ2 |
|
|
||||
|
95 |
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
divj1 |
= |
|
|
|
j1 |
|
|
|
|
x2 |
= |
1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
divj2 |
|
|
|
|
j2 |
|
|
|
|
x1 |
|
|
|
a3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, все явления, связанные с протеканием токов в разрядах, |
||||||||||||||||||||||||||||||||||||||||||||||
допускают использование законов подобия. Необходимо, кроме того, чтобы |
|
i1 |
= |
1 |
. |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
a3 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i2 |
|
|
|
||||
Это условие выполняется не всегда. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рассмотрим примеры элементарных процессов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
1. Ионизация |
газа |
электронным |
ударом. |
|
|
|
|
и = αиneue - число |
ионизаций, |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
αи |
|
|
p |
|
|
1 |
|
|||
осуществляемых электронами в одну секунду. Легко показать, что |
|
1 |
= |
|
1 |
= |
|
, |
||||||||||||||||||||||||||||||||||||||
αи |
2 |
p2 |
a |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
αи n1u1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
= |
|
1 |
|
|
|
|
|
|
= |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
αи n2u2 |
a3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, ионизация электронным ударом - процесс, который не нарушает |
||||||||||||||||||||||||||||||||||||||||||||||
правил подобия, и поэтому является разрешенным. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
2. Рекомбинация ионов с ионами при низких и высоких давлениях. Зависимость |
||||||||||||||||||||||||||||||||||||||||||||||
коэффициента рекомбинации αp от давления показана на рис. 45. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Имеется две области, в первой, при низких давлениях αp p , и во второй, при |
||||||||||||||||||||||||||||||||||||||||||||||
высоких давлениях, |
α |
|
|
1 |
. Для процесса рекомбинации объемный коэффициент |
|||||||||||||||||||||||||||||||||||||||||
p |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
согласно уравнению (49) составляет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
= |
dn |
= −α |
|
|
|
n2 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
i |
|
|
|
p |
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Отсюда для случая рекомбинации при низких давлениях имеем |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
p |
|
|
|
αp |
|
|
|
n2 |
|
|
|
|
1 |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
|
|
= |
|
|
|
1 |
|
|
1 |
|
= |
|
|
|
|
|
|
|
= |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
p |
|
|
α |
p2 |
2 |
|
|
a |
a |
4 |
|
|
|
a |
5 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Таким образом, этот процесс является запрещенным. Легко видеть, что для
области высоких давлений A = 13 , т.е. процесс рекомбинации ионов с ионами при a
высоком давлении протекает в соответствии с законами подобия.
96
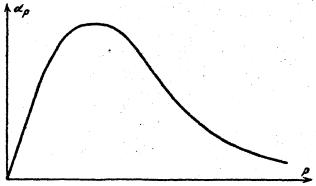
Рис. 45. Зависимость коэффициента рекомбинации положительных и
отрицательных ионов от давления газа.
97
Известные элементарные процессы были проверены на физическое подобие, т.е. разделены на разрешенные и запрещенные.
К разрешенным процессам следует отнести:
1)все виды движения заряженных частиц;
2)ионизацию ударами электронов и ионов;
3)возбуждение ударами электронов и ионов;
4)ионизацию и возбуждение Светом самого разряда;
5)рекомбинацию ионов с ионами при высоком давлении;
6)образование отрицательных ионов;
7)химические реакции без изменения числа молекул, например, N2+O2=2NO;
8)явления на пограничных поверхностях без изменения числа молекул;
9)удары второго рода при постоянном количестве примеси.
К запрещенным процессам относятся:
1)ступенчатая ионизация и возбуждение;
2)термическая ионизация (из-за ее ступенчатости);
3)рекомбинация ионов с ионами при низком давлении;
4)рекомбинация электронов с ионами;
5)химические реакции с изменением числа молекул;
6)явления на граничных поверхностях с изменением числа молекул;
7)местные нагревы газа.
Разрешенные процессы 1–4 и 8, 9 являются основными для многих разрядов. Запрещенные процессы 1,2,7 характерны для разрядов с большой плотностью тока. Удельный вес запрещенных процессов 3–6 обычно невелик.
Отсюда следует вывод: законы подобия применимы для слаботочных разрядов и неприменимы для сильноточных. При высоких и сверхвысоких частотах законы подобия применимы к разрядам с относительно небольшой плотностью заряженных частиц, что соответствует низкому уровню мощности. В разрядах с высоким уровнем мощности большую роль начинают играть ступенчатые процессы, а также электронноионная рекомбинация в объеме; эти процессы не подчиняются законам подобия. Подробное изложение законов подобия содержится в работах (28, 30, 31).
98
ГЛАВА V
ЛАВИННЫЙ РАЗРЯД И ПРОБОЙ ГАЗА
14. Лавинный разряд
Рассмотрим образование электронной лавины в промежутке, образованном плоскими параллельными электродами (рис. 46). Промежуток заполнен газом при давлении р и температуре Т, которым отвечает длина свободного пробега λ. Электрическое поле Е направлено перпендикулярно плоскостям электродов, и при малых величинах токов, когда влиянием объемного заряда можно пренебречь, не зависит от координаты x .
Разность потенциалов Е λ, пройденная электроном за среднюю длину свободного пробега, сравнительно велика, и удельный вес ионизирующих соударений, в общем числе соударений электронов в газе велик.
Начальные электроны появляются в газе за счет какого-либо ионизирующего фактора, или из катода, например, за счет облучения ультрафиолетовым светом. Рассмотрим движение одного из этих электронов (рис. 46). В электрическом поле энергия электрона будет быстро увеличиваться и в точке 1 окажется достаточной для ионизации атома; возникает второй электрон. Далее процесс многократно повторяется, и в результате один электрон вызывает появление лавины электронов и такого же числа положительных ионов.
Рассчитаем усиленный ток. На пути х начальный фотоэлектрический ток из катода I0 усилится до величины I. Прирост тока на пути dx составит
dI = Iαdx ,
где α - линейный коэффициент ионизации. Интегрирование этого уравнения для случая постоянных Е и α даст
I = Aeαx .
Постоянную интегрирования А находим из начальных условий: при х = 0, I = I0. Окончательно ток электронов для координаты х
I = I0eαx . |
|
Отсюда для тока электронов, приходящих на анод, получаем |
|
Iа = I0eαd . |
(84) |
99

Рис. 46. Электронная лавина в газе
100
