
Идентификация и диагностика систем
.pdfПри описании объектов, обладающих транспортным запаздыванием τ , в общем случае, дифференциальное уравнение (2.9) принимает вид:
an |
d n y(t −τ ) |
+ an −1 |
d n −1 y(t −τ ) |
+ ... + a0 y(t −τ ) = |
|
|
dt n |
|
dt n −1 |
|
|||
|
|
|
|
|
||
|
= b |
d mu(t) |
+ ... + b u(t), |
(2.11) |
||
|
dt m |
|
||||
|
m |
|
0 |
|
|
|
а передаточная функция, соответственно, определяется выражением:
|
|
|
m |
|
|
|
|
W ( p) = |
y( p) |
|
∑bi pi |
e |
− pτ |
|
|
= |
i =0 |
. |
(2.12) |
||||
u( p) |
n |
|
|||||
|
|
∑ai pi |
|
|
|
|
i =0
в) Уравнения в пространстве состояний Динамические процессы, наряду с дифференциальным уравнени-
ем n-го порядка (2.9), также можно описать системой n обыкновенных дифференциальных уравнений первого порядка:
|
|
|
|
dyi = ∑aij y j + ∑biju j , |
i =1,2,...n. |
|
(2.13) |
||||
|
|
|
|
|
|
n |
m |
|
|
|
|
|
|
|
|
dt |
|
j =1 |
j =1 |
|
|
|
|
|
Вводя в описание вектор состояний системы, представим модель |
||||||||||
в пространстве состояний в следующей матричной форме: |
|
|
|||||||||
|
|
d x |
= A(t)x(t) + B(t)u(t), |
x(t0 ) = x0 , t ≥ t0 |
|
|
|||||
|
|
dt |
(2.14) |
||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
y(t) = C(t)x(t) + D(t)u(t), |
|
|
|
|
|||||
где |
x(t) = [x1 (t) |
x2 (t) |
... |
xn (t)]T - вектор состояний размерностью |
|||||||
n; |
u(t) = [u1 (t) u2 (t) |
... |
um (t)] - вектор входов |
размерностью |
m; |
||||||
y(t) = [y1 (t) y2 (t) ... |
y p (t)]T - вектор выходов |
размерностью |
p ; |
||||||||
A(t)– матрица динамики системы размерностью [n ×n]; B(t) – распределительная матрица размерностью [n ×m]; C(t) – выходная матрица (матрица наблюдений) размерностью [p ×n]; D(t)– матрица «вход-выход» размерностью [p ×m].
31
Наиболее распространенной формой математической модели линейной динамической системы в пространстве состояний является система двух векторных уравнений (2.14). Первое уравнение - дифференциальное - задает поведение системы во времени, второе - алгебраическое – устанавливает связь выходной величины с вектором состояний и со входом.
С учетом воздействия внешней среды, при наличии входной аддитивной помехи v(t) и погрешностей измерения η(t) базовая формулировка модели имеет вид:
d x |
= A(t)x(t) + B(t)u(t) +V (t)v(t); x(t |
0 |
) = x ; t ≥ t |
0 |
; |
|
|
|
|||||
dt |
0 |
|
(2.15) |
|||
|
|
|
|
|||
y(t) = C(t)x(t) + D(t)u(t) +η(t),
где, помимо рассмотренных ранее обозначений, также присутствуют: v(t) – k -мерный вектор случайных воздействий - помех; V (t) - матрица размерностью [n ×k], описывающая канал прохождения по-
мехи; η(t) – p - мерный вектор шумов измерения.
Воздействия v(t) и η(t) , как правило, полагаются гауссовскими случайными процессами в виде белого шума.
Рассмотренная модель (2.15) может быть представлена следующей структурной схемой в пространстве состояний:
32
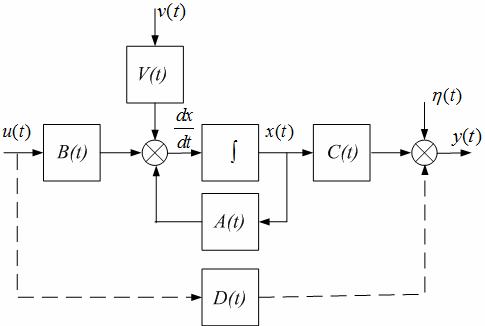
Рисунок 2.1 Структурная схема линейной динамической системы в пространстве
состояний при учете воздействий внешней среды
∫ – матричный интегратор
Если матрицы A(t), B(t),C(t), D(t) не зависят от времени t, то система называется стационарной.
Если часть входного воздействия u(t) пропорционально поступает на выход системы, т.е. D(t) ≠ 0 , то система называется несобственной. В динамических системах практически всегда D(t) = 0 . Такая система называется собственной или строго реализуемой.
2.4 Линейные динамические дискретные параметрические модели
Линейные динамические дискретные модели могут принимать следующий вид [3, 11, 13, 26, 42, 52, 72]:
а) Обыкновенные разностные уравнения Универсальной характеристикой для дискретных моделей являет-
ся разностное уравнение n-го порядка, где используется понятие разности как аналога понятию производной для непрерывных моделей: a0 y(k) + a1 y(k −1) +... + an y(k − n) =
33
= b0u(k) +b1u(k −1) +... +bmu(k − m), |
(2.16) |
где y(k),u(k) - значения выходной и входной величин в k-ый момент времени k =1,2...
б) Дискретные передаточные функции
Применяя оператор сдвига во времени z, задаваемый соотно-
шением y(k + i) = zi y(k) |
к конечно-разностному уравнению (2.16), |
|||||||
получают операторную форму дискретной модели: |
|
|
||||||
(a |
0 |
+ a z −1 |
+....a |
n |
z −n ) y(k) = (b |
+ b z −1 +.....b |
m |
z −m )u(k), (2.17) |
|
1 |
|
0 |
1 |
|
|||
Из (2.17) при нулевых начальных условиях можно получить дискретную передаточную функцию линейной системы, представляющую отношение z-изображений сигнала на входе к сигналу на выходе:
|
y(z) |
|
b |
|
+ b z −1 |
+.....b |
|
z −m |
|
|
W (z) = |
|
= |
0 |
1 |
m |
|
, |
(2.18) |
||
u(z) |
|
+ a z −1 |
|
z −n |
||||||
|
|
a |
0 |
+.....a |
n |
|
|
|||
|
|
|
|
1 |
|
|
|
|
||
где, как и для передаточной функции непрерывной системы, обычно должно выполняться условие n ≥ m .
Применяется запись передаточной функции в матричной форме
|
W (z) = |
B(z−1) |
, |
(2.19) |
|
A(z−1) |
|||
|
|
|
|
|
n |
m |
|
|
|
где A(z−1 ) = ∑ai z−i , |
B(z−1 ) = ∑bi z−i . |
|
|
|
i=0 |
i=0 |
|
|
|
Учет запаздывания в объекте управления приводит к появлению задержки в управляющем сигнале на d периодов квантования в разностных уравнениях
a0 y(k) + a1 y(k −1) +... + an y(k −n) =
= b0u(k − d) +b1u(k − d −1)... +bmu(k −d − m) |
(2.20) |
|||||
и в передаточных функциях |
|
|
|
|
||
W (z) = |
y(z) |
= |
B(z−1) |
z−d . |
(2.21) |
|
u(z) |
A(z−1) |
|||||
|
|
|
|
|||
в) Уравнения в пространстве состояний
34
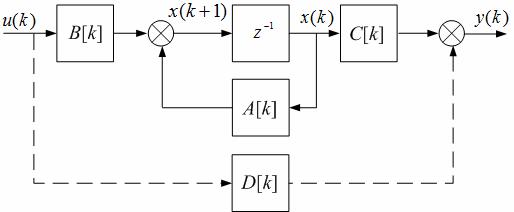
Используя для описания динамики дискретного объекта дискретные переменные состояния, образующие n - мерный вектор состояния x(k) = [x1 (k) x2 (k) ... xn (k)]T , получают описание объекта в пространстве состояний в следующей векторно-матричной форме:
x[k +1] = A[k]x[k] + B[k]u[k]; x[k0 |
] = x0 |
; k ≥ k0 |
; |
(2.22) |
y[k] = C[k]x[k] + D[k]u[k] , |
|
|
|
|
|
|
|
|
где u[k] Rm , y[k] R p , матрицы A[k], B[k],C[k], D[k] имеют размерности [n ×n], [n ×m], [p ×n] и [p ×m] соответственно.
Структурное представление модели (2.22) приведено на рисунке
2.2.
Рисунок 2.2 Дискретная модель объекта в пространстве состояний
б) Авторегрессионные модели со скользящим средним При анализе стохастических систем исходные данные являются
результатом цифровой обработки отдельных реализаций случайного процесса. В соответствии с этим, в современной теории цифровых систем получили широкое распространение цифровые параметрические стохастические модели авторегрессии и скользящего среднего (АРСС-модели). Эти модели используются для изучения временных рядов, определения статистических характеристик этих рядов и широко применяются в управлении, экономике, при обработке звуковых сигналов [4, 12, 15, 28, 53]. Они достаточно просты, удобны в приме-
35
нении и обычно содержат небольшое число параметров, необходимых для процедуры оценивания.
При использовании АРСС-моделей предполагают, что система подвержена влиянию внешних помех типа белого шума e(k), действие которых можно отобразить аддитивной случайной составляющей выходного сигнала , соответствующей прохождению белого шума через фильтр с некоторой передаточной функцией
W(z −1 ) = D(z −1 ) [25, 26, 27, 49]. Структурная схема такой модели мо-
фC(z −1 )
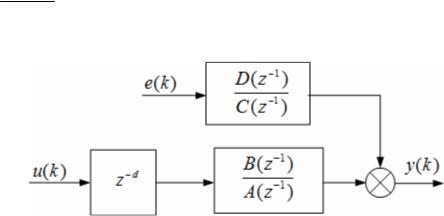
жет быть представлена в следующей форме:
Рисунок 2.3 Структурная схема полной модели дискретного объекта управления
Рисунок 2.3 отвечает полной модели дискретного объекта управления с запаздыванием с учетом шума измерений, которой соответствует следующая символьная форма:
|
|
B(z−1) |
−d |
|
|
|
D(z−1) |
(2.23) |
||
y(z) = |
|
|
z |
|
u(z) |
+ |
|
|
e(z). |
|
|
A(z−1) |
|
C(z−1) |
|||||||
При решении задачи идентификации в такой постановке наряду с |
||||||||||
параметрами объекта |
A(z −1 ), B(z −1 ) |
|
определению также |
подлежат |
||||||
параметры модели фильтра помехи C(z−1), D(z−1 ) (его передаточной функции), что зачастую приводит к сложностям вычислительного характера. Поэтому часто в практике идентификации используют более простую усеченную модель фильтра, в которой в качестве канала прохождения помех используется звено с передаточной функцией
36

вида |
D(z−1 ) |
или |
1 |
. Такое упрощение позволяет уменьшить раз- |
|
A(z−1 ) |
|||
|
A(z−1 ) |
|
||
мерность задачи, и тем самым упростить методику ее решения. В этом случае усеченная модель для одномерного стохастического объекта без запаздывания с передаточной функцией фильтра, равной
D(z−1 ) , имеет вид:
A(z−1 )
A(z−1 )y(z) = B(z−1 )u(z) + D(z−1 )е(z) |
(2.24) |
или в развернутой форме записи |
|
a0 y(k) + a1 y(k −1) +.......an y(k −n) = b0u(k) +b1u(k −1) + |
|
+... + bmu(k − m) + e(k) + d1e(k −1) +... + d pe(k − p), |
(2.25) |
где p- число оцениваемых параметров шума; e(k)- дискретные значения процесса типа белого шума с единичной дисперсией в k-ый момент времени.
При использовании в качестве фильтра помехи звена с переда-
точной функцией |
1 |
|
, получается АРСС-модель следующего вида: |
|
|
|
|||
|
A(z −1 ) |
|
||
|
|
A(z−1)y(z) = B(z−1)u(z) +е(z) |
(2.26) |
|
или |
|
|
|
|
|
a0 y(k) + a1 y(k −1) +... + an y(k − n) = |
|
||
|
= b0u(k) + b1u(k −1) +... + bmu(k − m) + e(k). |
(2.27) |
||
Частными случаями АРСС-моделей (2.26), (2.27) являются следующие:
при m = 0 имеем модель авторегрессии (АР):
a0 y(k) + a1 y(k −1) +.......an y(k − n) = b0u(k) + e(k) |
(2.28) |
или |
|
A(z−1)y(z) = bu(z) +е(z). |
(2.29) |
При n = 0 получается модель скользящего среднего (СС): |
|
a0 y(k) = b0u(k) + b1u(k −1)........bmu(k − m) + e(k) |
(2.30) |
или |
|
ay(z) = B(z−1)u(z) +е(z). |
(2.31) |
37
Отметим, что цифровые модели авторегрессии также используются для моделирования помехи при преобразовании последовательности типа белого шума в случайные последовательности с заданными характеристиками. В общем случае, беря за основу уравнение (2.23), получают АРСС - модель случайных помех в измерениях:
v(z) =Wф(z−1)e(z) = |
D(z−1) |
e(z), |
(2.32) |
|
|||
|
C(z−1) |
|
|
где e(z) - белый шум с единичной дисперсией; v(z) |
- коррелирован- |
||
ный (цветной) шум.
Из (2.32) по аналогии (2.28) - (2.31) могут быть получены частные случаи АР – или СС – моделей помех в измерениях.
2.5 Нелинейные динамические модели
Класс нелинейных динамических систем по сравнению с линейными значительно шире, т.к. в этих системах протекают многообразные явления и процессы, нехарактерные для линейных систем. Вследствие этого для описания таких систем становится неприменим математический аппарат теории линейных систем. Поэтому при решении задачи получения математических моделей нелинейных систем используются следующие два основных подхода [64]. Один подход заключается в получении приближенного математического описания линеаризованной модели, в определенном смысле эквивалентной исходной нелинейной модели, с помощью методов линеаризации: гармонической, статистической, малых приращений. Наиболее применим такой подход для объектов, имеющих гладкие характеристики, и процессов, протекающих при небольших отклонениях и возмущениях относительно номинальных режимов функционирования.
При втором подходе математическая модель рассматривается как существенно нелинейная. В этом случае наиболее распространенными видами моделей являются следующие.
а) Нелинейные дифференциальные уравнения.
38
Для непрерывного одномерного объекта управления связь между входным и выходным сигналами записывается, в общем виде, неявным выражением:
& && |
(n) |
& && |
(m) |
) = 0, |
(2.33) |
F( y, y, y,....y |
|
,u,u,u,......u |
|
где F - некоторый нелинейный оператор (n + m +1) аргумента, который требуется идентифицировать. Если возможно, то проводится параметризация нелинейной модели (2.33) на основе структурирования F с введением некоторого вектора параметров βi :
F ( y, y&,....y(n) ,u,u&,......u(m) , β1, β2 ,.....βl ) = 0, |
(2.34) |
где βi , i =1...l - параметры модели.
В этом случае задача идентификации сводится к определению оператора F и к оцениванию его вектора параметров βi , i =1...l .
Для нелинейного дискретного объекта строятся аналогичные нелинейные разностные уравнения.
б)Модели Гаммерштейна.
Такие модели нелинейных инерционных объектов строятся в предположении, что нелинейность и инерционность объекта можно разделить и представить объект в виде последовательной комбинации двух звеньев: нелинейного безынерционого и динамического линейного. Модели «вход-выход» для таких объектов в одномерном стационарном случае могут иметь два варианта описания:
∞ |
|
|
y(t) = ∫ w(τ )F [u(t −τ )]dτ |
|
(2.35) |
0 |
|
|
или |
|
|
∞ |
|
(2.36) |
y(t) = F ∫ w(τ )u(t −τ )dτ |
|
|
0 |
|
|
где w(t) - импульсная переходная функция линейного звена; F(u) - статическая характеристика нелинейного звена.
Структурное представление моделей объекта для каждого из вариантов описания приведено на рисунке 2.4.
39
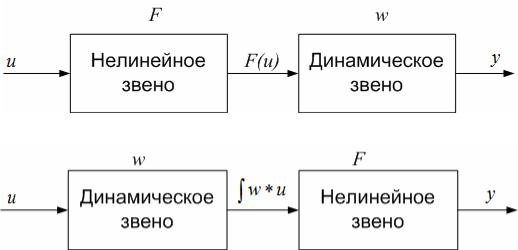
а
б
Рисунок 2.4.
Структурная схема модели Гаммерштейна при описании вида (2.35) –(а)
и вида (2.36) –(б).
в) Разложение Вольтерра.
При данном способе описания зависимость между входом u(t) и выходом y(t) представляется рядом [17, 41]
t t t
y(t) = ∫w1(τ)u(t −τ)dτ + ∫∫w2 (τ1,τ2 )u(t −τ1)u(t −τ2 )dτ1dτ2 +..., (2.37)
0 0 0
где w1 (τ), w2 (τ1 ,τ2 ), w3 (τ1 ,τ2 ,τ3 ) - обобщенные весовые функции (ядра) i – го порядка. Такой ряд (2.37) носит название ряда Вольтерра. Разложение в ряд Вольтерра является непосредственным обобщением линейной модели в форме интеграла свертки на нелинейные объекты. Задача идентификации при этом состоит в определении обобщенных весовых функций wi (t1 ,t2 ,...ti ), i =1,2,.... Для нестационарного объекта ядра будут зависеть от t.
г) Описание в пространстве состояний.
В общем случае, уравнения состояния для конечномерных непрерывных систем записываются в следующем виде:
dx = f (x(t),u(t),t); x(t |
0 |
) = x ; t ≥ t |
0 |
; |
|
dt |
0 |
|
(2.38) |
||
|
|
|
|
y(t) = g(x(t),u(t),t).
40
