978-5-7764-0767-3

ды условий активизации других вершин. Простые (элементарные) связи пе-

редают сигнал активизации без искажения, вмешательства, изменения его временных характеристик, что приводит к выделению многих вершин и, тем самым, создает множество интерпретаций, возможных действий для текущей ситуации. Особенно это проявляется в отношении вершин, являющихся обобщением более простых по составу вершин. Для сокращения объема воз-

можных интерпретаций должны активизироваться не все связи, а только те,

которые соответствуют содержанию (контексту) текущей (рассматриваемой)

ситуации. С этой целью элементарная связь должна усложниться. Существу-

ющая связь между вершинами разрывается и в разрыв вставляется мнимая вершина, которая имеет один вход условий активизации, один выход для сигнала о собственной активизации и множество входов, определяющих условие возможности передачи сигнала активизации. Условие, определяю-

щее возможность передачи сигнала активизации может быть представлено,

как простым, так и сложным логическим выражением.

Содержание описания составной связи аналогично описанию вершины

[27,30] и может включать:

–NR – имя рассматриваемой связи,

–PRUS – множество признаков, определяющих возможность передачи сигнала активизации),

–PSUS – признак активизации мнимой верщины рассматриваемой связей,

–LN_LS – список имен вершин, от которых поступает сигнал активиза-

ции,

–LN_HS – имена вершин, к которым идет сигнал активизации,

–LN_Ex – список примеров, активизирующих вершину связи,

–W – весовые коэффициенты.

Интегрированная модель представления знаний позволяет на основе элементарных связей создать составные связи между сущностями действи-

тельности. В процессе формирования составных связей можно выделить сле-

дующие основные этапы:

191

выделение вершин-сущностей из проблемной области;

выделение подмножества связей рассматриваемой вершины-сущности с другими вершинами-сущностями;

анализ каждой связи:

oесли рассматриваемая связь не является элементарной, то определение и описание ситуации при которой эта связь активизирована. Пред-

ставление этой ситуации в виде предусловия для мнимой вершины-

сущности;

o добавление в предусловие самой связи;

oвыход мнимой вершины-сущности соединить с требуемой вершиной-

сущностью.

Создание сложных связей является не простой и ответственной задачей,

поскольку неверно сформированная связь может оказать негативное воздей-

ствие на результаты работы всей базы знаний.

Для снижения вероятности ошибок в сложной связи целесообразно ис-

пользовать вспомогательные инструменты, как для создания новых сложных связей, так и для анализа существующих. В качестве таких дополнительных инструментов, рассматриваются сети Петри [11].

Анализ сложных связей. Сложная связь представляет собой связь, состо-

ящую из двух и более элементарных связей. Строгое определение элементар-

ной связи будет дано ниже. Принимается, что сложная связь и составная связь являются синонимами.

В одном из подходов к проектированию и анализу различных систем,

сети Петри используются, как вспомогательный инструмент анализа суще-

ствующих систем. При создании анализируемой системы – сложной связи,

используются общепринятые методы проектирования. Полученная сложная связь моделируется сетью Петри, а затем разработанная модель сложной свя-

зи анализируется. При обнаружении в сложной связи недостатков, их устра-

нение происходит путем модификации сложной связи. Модифицированная сложная связь опять моделируется и проводится анализ. Если результаты

192

анализа являются неудовлетворительными, то модификация сложной связи,

построение модели сложной связи в виде сети Петри и ее анализ повторяют-

ся снова. Эти этапы свойственны для уже созданных сложных связей. В этом случае необходимы методы моделирования сложных связей сетями Петри.

При создании новых вершин сложных связей используется другой под-

ход, при котором предполагается построение сложной связи сразу в виде се-

ти Петри. В этом случае методы анализа применяются только для создания сложной связи, не содержащей ошибок. Затем сеть Петри преобразуется в описание сложной связи в формате интегрированного метода представления знаний. Для этого подхода необходимы методы формирования сложной свя-

зи в виде сети Петри и методы реализации сетей Петри в формате интегриро-

ванного подхода к представлению знаний.

Действительность состоит из множества сущностей, среди которых можно выделить два типа: сущности-действия – Сд и сущности признаки Сп.

Эти два типа сущностей присутствуют в составной связи. С использованием выделенных типов сущностей можно определить элементарную связь.

Определение. Элементарная связь представляет собой сущность-

действие, у которой постусловие повторяет предусловие, т.е. ПсУ=ПрУ.

Сущность, для моделирования сетью Петри, в формате интегрированно-

го метода представления знаний, минимально может определяться тремя элементами в следующем виде:

Сщ = (И, ПрУ, ПсУ), где

И = (и1, и2, …, иv) – конечное множество имен сущностей, v ≥ 0;

ПрУ = (ПрУ1, ПрУ2, …, ПрУv) – конечное множество предусловий сущ-

ностей, v ≥ 0;

ПсУ = (ПсУ1, ПсУ2, …, ПсУv) – конечное множество постусловий сущ-

ностей, v ≥ 0.

Составная связь СтС является пятеркой: СтС = (ИСтС, СП, СД, ПрУ, ПсУ), где

193

ИСтС = (и1, и2, …, иv1) – конечное множество имен сущностей составных связей, v1 ≥ 0;

СП = (сп1, сп2, …, спn) – конечное множество сущностей-признаков, n ≥ 0;

СД = (сд1, сд2, …, сдm) – конечное множество сущностей-действий, m ≥ 0;

ПрУ = (ПрУ1, ПрУ2, …, ПрУv1) – конечное множество предусловий сущ-

ностей составных связей, v1 ≥ 0;

ПсУ = (ПсУ1, ПсУ2, …, ПсУv1) – конечное множество постусловий сущ-

ностей составных связей, v1 ≥ 0;

ПрУ: СД СПвх входная функция, сопоставляющая сущности-

действию СД множество ее входных признаков;

ПсУ: СД СПвых выходная функция, сопоставляющая сущности-

действию СД множество ее выходных признаков.

Сущность-признак сп СП является входом для сущности-действия сд СД, если сп ПрУ(сд).

Сущность-признак сп СП является выходом для сущности-действия сд СД, если сп ПсУ(сд).

Структура сети Петри для сложной связи определяется ее сущностями-

признаками, сущностями-действиями, предусловиями и постусловиями.

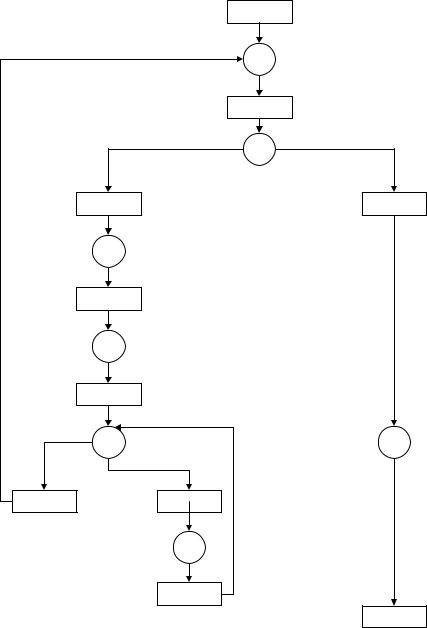
Сеть Петри, моделирующая сложную связь «находит» между вершина-

ми «робот» и «объект», в виде алгоритма поиска роботом объекта, представ-

лена на рис. 4.12.

Построенная сеть Петри теперь может использоваться для анализа моде-

лируемой сложной связи. Основными подходами к анализу сетей Петри яв-

ляются [11] методы, основанные на использовании дерева достижимости,

подход, основанный на матричном представлении сетей Петри, решении матричных уравнений и методах преобразования сетей.

Формирование сложных связей с помощью сетей Петри. Другой подход

[19], к использованию сетей Петри, заключается в построении сложной связи в виде сети Петри, исследовании полученной сети Петри на наличие ошибок и в последующем преобразовании сети Петри в сложную связь. Для этого

194

подхода необходим метод построения сложной связи в виде сети Петри и преобразовании сети Петри в описание сложной связи в формате интегриро-

ванного метода представления знаний. Составная связь представляется сетью Петри с использованием двух основополагающих понятий: условия и собы-

тия.

Рис. 4.12. Сеть Петри, моделирующая сложную связь «находит»

Построенная сеть Петри теперь может использоваться для анализа мо-

делируемой сложной связи. Основными подходами к анализу сетей Петри являются [11] методы, основанные на использовании дерева достижимости,

195

подход, основанный на матричном представлении сетей Петри, решении матричных уравнений и методах преобразования сетей.

Формирование сложных связей с помощью сетей Петри. Другой подход

[19], к использованию сетей Петри, заключается в построении сложной связи в виде сети Петри, исследовании полученной сети Петри на наличие ошибок и в последующем преобразовании сети Петри в сложную связь. Для этого подхода необходим метод построения сложной связи в виде сети Петри и преобразова-

нии сети Петри в описание сложной связи в формате интегрированного метода представления знаний. Составная связь представляется сетью Петри с исполь-

зованием двух основополагающих понятий: условия и события.

Состояние сложной связи описывается совокупностью условий. Функ-

ционирование (срабатывание) сложной связи состоит в осуществлении по-

следовательности событий. Для возникновения события необходимо выпол-

нение некоторых условий, называемых предусловиями. Возникновение со-

бытий может привести к выполнению условий, называемых постусловиями.

В содержательном плане переходы соответствуют событиям, которые харак-

терны составной связи, а позиции – условиям их возникновения. Переход

(событие) характеризуется определённым числом входных и выходных пози-

ций, соответствующих предусловию и постусловию данного события. Сово-

купность переходов, позиций и дуг позволяет описать статическую сложную связь. Для описания динамики используется еще один объект – маркер, или фишка позиции. Наличие фишки в некоторой позиции интерпретируется как истинность условия, соответствующего данной позиции. Расположение мар-

керов в позициях называется разметкой сети. Текущее состояние исследуе-

мой сложной связи определяется распределением маркеров по позициям се-

ти, а динамика поведения системы отображается перемещением маркеров по позициям сети. Переход, не имеющий ни одной входной позиции, называется истоком, а переход, не имеющий ни одной выходной позиции – стоком.

Для того, чтобы событие произошло, необходимо появление ситуации в которой это событие может быть реализовано. Сама ситуация определяется

196

как совокупность некоторых условий возникновения события. При синтезе сети Петри каждому из событий ставится в соответствие переход сети Петри,

имеющий соответствующий номер. Переходы последовательно связываются друг с другом входными/выходными позициями.

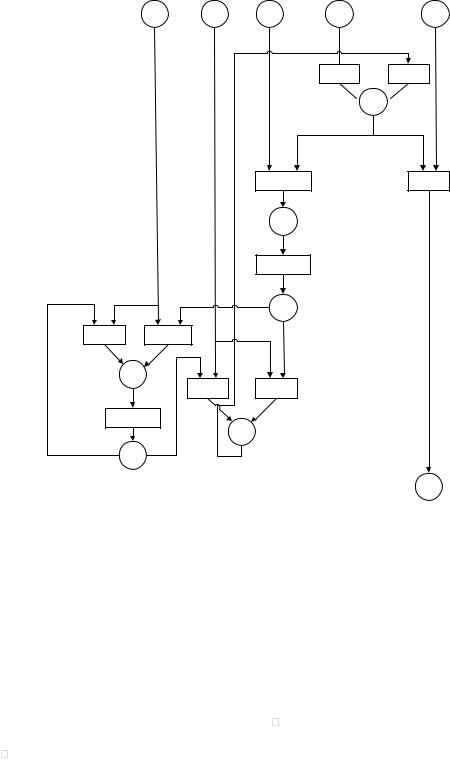
Полученная сеть Петри представлена на рис. 2. Созданная модель синте-

зирована из предположения, что условия возникновения событий всегда вы-

полняются. В силу этого предположения не требуется вводить новые пози-

ции, которые соответствуют набору условий выполнения событий t1-1, t1-2, t2,

… , t6-1, t6-2 , t7.

При исследовании синтезированной сети Петри, для сложной связи, мо-

гут применяться методы анализа, позволяющие определять наличие или от-

сутствие таких основных свойств сетей Петри, как безопасность и ограни-

ченность, сохраняемость, достижимость, живость. Для моделей составных связей наибольший интерес представляет анализ достижимости – возмож-

ность перехода из начального состояния в конечное (срабатывание сложной связи). Возможно решение задачи по выявлению тупиковых ситуаций в со-

ставных связях. Для рассматриваемого примера такой тупиковой ситуацией может быть нахождение объекта, который не находится на месте, а движется с роботом в одном направлении с той же скоростью. Понятно, что при не-

ограниченных ресурсах робот будет двигаться к объекту бесконечно. При обнаружении такой ситуации могут приниматься меры (введение дополни-

тельных условий для выявления факта невозможности реализации действия)

для своевременного отказа от выполнения намеченных действий.

Основными методами анализа свойств достижимости являются:

–построение дерева достижимости;

–метод матричных уравнений.

Для синтезированной сети Петри (рис. 4.13) дерево достижимости пред-

ставлено на рис. 4.14. Из основных свойств сетей Петри для сложных связей могут использоваться следующие: живость – отсутствие тупиковых состоя-

ний, исключая выходное (целевое) состояние сложной связи; безопасность –

197

метки вершин включают только «0» и «1», что означает отсутствие зацикли-

ваний; правильность – сеть безопасна и живая; пассивность переходов – пе-

реходу не соответствует ни одной дуги графа.

t1-1 t1-2

s1

Рис. 4.13. Синтезированная сеть Петри

Методы матричных уравнений. Альтернативным по отношению к опре-

делению сети Петри PN в виде (S, T, I, O) является определение сети Петри

PN в виде двух матриц D- и D+, представляющих входную и выходную функции I и O. Каждая из матриц D- и D+ имеет m = │T│ строк (по одной на переход и n = │S│ столбцов (по одному на позицию). Матричный вид сети Петри PN = (S,T,I,O) задаётся парой (D , D+), где

D [k,i] = ^#(si,tk) – кратность дуги, ведущей из позиции pi в переход tk;

D+[k,i] = #^(si,tk) – кратность дуги, ведущей из перехода tk в позицию si,

для произвольных 1 ≤ k ≤m, 1 ≤ i ≤n.

198

µ0=(1,0,1,0,1,0,0,0,0,0,0,0) ↓ t1-1

µ1=(1,0,0,0,1,1,0,0,0,0,0,0) ↓ t3

µ2=(1,0,0,0,1,0,0,1,0,0,0,0) ↓ t4

µ3=(1,0,0,0,1,0,0,0,1,0,0,0) ↓ t5-2

µ4=(1,0,0,0,1,0,0,0,0,1,0,0) ↓ t1-2

µ1=(1,0,0,0,1,1,0,0,0,0,0,0) ↓ t3

µ2=(1,0,0,0,1,0,0,1,0,0,0,0) ↓ t4

µ5=(1,0,0,1,0,0,0,0,1,0,0,0) ↓ t6-2

µ6=(1,0,0,1,0,0,0,0,0,0,1,0) ↓ t7

µ7=(1,0,0,0,1,0,0,0,0,0,0,1) ↓ t5-1

µ4=(1,0,0,0,1,0,0,0,0,1,0,0) ↓ t1-2

µ1=(1,0,0,0,1,1,0,0,0,0,0,0) ↓ t3

µ2=(1,0,0,0,1,0,0,1,0,0,0,0) ↓ t4

µ8=(0,1,0,0,1,0,0,0,1,0,0,0) ↓ t9

µ9=(0,1,0,0,1,0,0,0,0,1,0,0,) ↓ t1-2

µ10=(0,1,0,0,1,1,0,0,0,0,0,0,) ↓ t2

µ11=(0,1,0,0,1,0,1,0,0,0,0,0)

Рис. 4.14. Дерево достижимости для синтезированной сети Петри

Матричная теория сетей Петри является инструментом для исследова-

ния и решения проблемы достижимости. Положительным моментом матрич-

ного подхода к анализу сетей Петри является компактность представления информации и высокая степень формализации.

Приведение синтезированной сети Петри к формату интегрированного метода представления знаний. Каждый переход и каждая позиция сети Петри представляют собой сущность. Описание сущностей составной связи, синте-

зированной в виде сети Петри, происходит в следующей последовательно-

сти.

1.Формируется/запрашивается имя рассматриваемой сущности.

2.По входным в позицию или переход дугам формируется предусловие сущности: условие включает имя сущности (перехода или позиции, если их имена идентичны) откуда берет начало дуга и признак его активности – «1».

Таким образом формируется каждое условие из предусловий сущности.

3. По выходным дугам формируется постусловие рассматриваемой сущности. Для обеспечения безопасности сети Петри признаки активности

199

могут соответствовать признаку активности только для одной ситуации. В

качестве постусловия берется признак срабатывания перехода.

4. Cписок имен нижнего уровня формируется из имен сущностей – при-

знаков, используемых в предусловиях.

5. Список имен верхнего уровня формируется из имен элементов сети Петри в условиях которых присутствует признак срабатывания рассматрива-

емой сущности (перехода,

Сформированная составная связь «Найти объект» не является конкрет-

ной, а позволяет создавать связь для всех допустимых ситуаций.

Развитие элементной базы, технологий производства вычислительных средств, разработка новых программно-аппаратных платформ позволяет со-

здавать приложения для решения задач реальной сложности. В полной мере эти возможности относятся и к интеллектуальным системам и, в частности, к

системам, основанным на знаниях. Размер баз знаний современных интел-

лектуальных информационных систем постоянно увеличивается и, соответ-

ственно, цена ошибки возрастает. Привлечение экспертов для выявления и исправления ошибок становится все более затратным процессом. С помощью рассмотренных методов возможно добавление новых сложных связей с ис-

пользованием имеющихся, что позволяет описывать предметные области для задач реальной сложности. Анализ новых сложных связей с применением се-

тей Петри позволяет исключать ошибки, влияющие на формирование реше-

ний в динамической интеллектуальной системе.

Перспективным направлением развития исследований является форма-

лизация процессов создания корректно построенных баз знаний и реализации этих процессов в вычислительных средах: локальных, распределенных. Со-

здание корректно построенных баз знаний может выполняться, как с помо-

щью классических технологий, так и с применением новых, например, об-

лачных вычислений.

200