Вопросы теоретического минимума1

Значения констант

1.Среднее число вторичных нейтронов в реакторе на тепловых нейтронах при делении ядер U-235 – 2,4; 239-Pu – 2,9.

2.Среднее число вторичных гамма квантов в реакторе на тепловых нейтронах при делении ядер U- 235 – 7,5; 239-Pu – 8,0.

3.Средняя энергия вторичных нейтронов при делении – 2 МэВ.

4.Средняя энергия вторичных гамма квантов при делении – 0,9 МэВ.

5.Средняя энергия, выделяющаяся при делении, - 200 МэВ.

6.Энергия максимума спектра нейтронов деления в реакторе на тепловых нейтронах – 1 МэВ.

7.Коэффициент перевода эВ в Дж – 1,6·10-19.

8.% доля запаздывающих нейтронов при делении ядер U-235 – 0,67%, Pu-239 – 0,21%.

9.Число Авогадро – 6,02·1023 1/моль.

10.Значение, принятое для предельно допустимой мощности дозы излучения, - 0,4 мЗв/нед.

Размерности и определения величин

1.Поток нейтронов – это среднестатистическое число нейтронов, энергия которых лежит в

единичном интервале E, направление полета – в единичном угловом диапазоне и которые в единицу времени пересекают воображаемую единичную площадку, расположенную в точке таким образом, что нормаль к площадке совпадает c 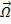. Ф = [нейтрон/м²·страд·эВ·с]

2.Микроскопическое сечения взаимодействия ядерной реакции х (характеристика ядра) – это

вероятность нейтрону испытать на бесконечно тонкой пластине взаимодействие типа х, отнесенная к поверхностной плотности ядер в данной пластине. σ = [см2]

3.Макроскопическое сечение взаимодействия с ядрами среды типа х (характеристика среды) – это вероятность нейтрону провзаимодействовать в среде, пройдя элементарный путь l, отнесенная к длине этого пути. ∑ = [1/см]

4.Микроскопический линейный коэффициент ослабления ядерной реакции типа х – это вероятность

гамма кванту испытать на бесконечно тонкой пластине взаимодействие типа х, отнесенная к поверхностной плотности ядер в данной пластине. µ = [см2]

5.Макроскопический линейный коэффициент ослабления с ядрами среды типа х – это вероятность гамма кванту провзаимодействовать в среде, пройдя элементарный путь l, отнесенная к длине этого пути. ∑ = [1/см]

6.Период полураспада радиоактивного изотопа – это время, за которое распадается половина ядер, первоначально находящихся в образце. Т1/2 = [лет]

7.Поглощенная доза излучения или доза – это энергия, переданная излучением защищаемому объекту, отнесенная к массе объекта. D=dW/dm; [Дж/кг]=Гр [1Гр=100рад]

8.Единица эквивалентной дозы излучения – 1 Зиверт=100бэр– эквивалентная доза, создаваемая биологической тканью образцовым (эталонным) излучением с поглощенной дозой 1 Грей. Образцовое (эталонное) излучение – рентгеновское излучение с Е>200кэВ

9.Сечение выведения материала – это некий коэффициент в экспоненте в формуле:

D D0 exp( remd ) , где:

D0 – эквивалентная доза нейтронов источника перед защитой с энергией больше 0,3 МэВ, распределенных по спектру деления; D – эквивалентная доза всех нейтронов за защитой;

d – толщина защиты. = [1/см] – характеристика защитной системы

Модель сечения выведения – это приближенный метод расчета дозы нейтронов за защитой от источника быстрых нейтронов

10.Дозовый фактор накопления защиты (безразмерная величина) – это отношение эквивалентной дозы гамма-квантов всех энергий за защитой (т.е. и рассеянных и нерассеянных гамма-квантов) (Dн/р+Dр) к эквивалентной дозе нерассеянных гамма-квантов за защитой (Dн/р).

ВD=Dполн / Dн/р = (Dн/р+Dр)/ Dн/р = 1+ Dр/ Dн/р ; ВD всегда > 1

11. Коэффициент качества излучения (безразмерная величина) – это отношение эквивалентных доз рассматриваемого и эталонного излучений, если их поглощенные дозы равны.

k= Dэкв рассм/Dэкв этал

Dэтал=Dрассм

Законы и соотношения

1.Закон радиоактивного распада. Скорость распада ядер радиоактивного изотопа в образце прямо пропорциональна числу ядер этого изотопа в образце.

2.Ядерная плотность (ρяд) через массовую плотность (ρмас) материала:

3.Макроскопическое сечение взаимодействия (Σ) через микроскопическое (σ):

4.Поглощенная доза излучения (D):

D=dW/dm, где W- энергия, переданная излучением защищаемому объекту, m – масса объекта

5.Эквивалентная доза излучения (Dэкв) через поглощенную дозу излучения (D): Справедливо только численно:

6.Эквивалентная доза излучения (Dэкв) через поток излучения (Ф):

S/m = µэн - коэффициент поглощения излучения; Ф = [1/см²·страд·эВ·с]

7.Сечение выведения материала – смотри 2.9.

доля i-го изотопа в смеси

8.Дозовый фактор накопления защиты – смотри 2.10.

9.Распределение потока нерассеянного излучения в однородной неразмножающей пластине. Задан моноэнергетический стационарный источник излучения на одной из поверхностей пластины, перпендикулярный этой поверхности.

10.Распределение потока нерассеянного излучения в однородной неразмножающей пластине. Задан моноэнергетический источник излучения, равномерно распределенный по объему пластины, направленный перпендикулярно поверхностям пластины.

11. Групповое сечение:

t (E)S (E)dE

Сечение межгруппового рассеяния:

13. Представление угловой зависимости потока в методе сферических гармоник. где Pm(µ) – полином Лежандра

Стационарное уравнение переноса нейтронов для задач

(названия и зависимости от переменных входящих величин, граничные условия)

1.для задачи из п.III.9 – смотри 3.9.

2.для задачи из п.III.10 – смотри 3.10. Для всех последующих задач:

3.для надкритической системы, ограниченной поверхностью R и окруженной вакуумом:

4. для подкритической размножающей системы, ограниченной поверхностью R и окруженной вакуумом. Задан источник излучения на поверхности системы.

Задан источник излучения, распределенный по объему.

5. для неразмножающей системы, ограниченной поверхностью R и окруженной вакуумом. Задан источник излучения на поверхности системы.

Задан источник излучения, распределенный по объему системы.

Задан источник излучения, распределенный по объему системы.

Задан источник излучения, распределенный по объему системы.