7.Вынужденные колебания. Уравнение вынужденных колебаний. Векторная диаграмма для вынужденных колебаний. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы. Резонанс.

Вынужденные колебания - это колебания, происходящие под действием периодического внешнего воздействия.

Внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.

Периодическая внешняя сила может изменяться во времени по различным законам.

Дифференциальное уравнение, описывающее вынужденные колебания

Изобразим эти колебания с помощью векторов, амплитуды которых получаются после умножения на2β, а - ξ на ω²₀

вправо направим вектор длиной ω²₀A, изображающий функцию ω²₀A · Cos( ωt - φ) , начальная фаза которой равна "минус фи".Т.к., то.Таким образом, амплитуда вынужденных колебаний изменяется с изменением частоты внешнего воздействия. При определенной частоте амплитуда достигает максимума. Это явление называется резонансом, а соответствующая частота -ω_рез - резонансной. Для определения ω_рез исследуем функцию A(ω) на максимум, для этого достаточно найти минимум знаменателя у выражения A(ω) . Возьмем от него производную по и приравняем к нулю:, откуда:. При2β² > ω²₀ резонанс отсутствует (ω_рез - мнимое число).

8.Определение волны. Продольные и поперечные волны. Волновое уравнение. Решение волнового уравнения. Классификация волн по их форме.

9. . Монохроматическая волна. Плоские монохроматические волны. Фаза волны. Волновая поверхность. Длина волны, волновое число, волновой вектор. Сферические волны.

w(t—x/v)+φ₀ – фаза плоской волны

Волновой вектор — вектор, направление которого перпендикулярно фазовому фронту бегущей волны, а абсолютное значение равно волновому числу.

k=2π/λ=2π/vT=w/v – волновое число

Монохроматическая волна — строго гармоническая (синусоидальная) волна с постоянными во времени частотой, амплитудой и начальной фазой.

Длина волны.

Сферические волны.

Фазовая скорость.

10.Энергия упругой волны. Поток и плотность потока энергии. Вектор Умова. Принцип суперпозиции волн. Стоячие волны. Собственные частоты, гармоники. Узлы и пучности стоячей волны. Звуковые волны. Эффект Доплера для звуковых волн (без вывода). Волновое уравнение для электромагнитного поля в однородной изотропной среде (без вывода). Скорость электромагнитных волн. Показатель преломления.

Энергия упругой волны

         Пусть в некоторой  среде распространяется продольная волна    . (7.а) Выделим в среде элементарный объём ∆V, настолько малый, чтобы скорость движения и деформацию во всех точках этого объёма можно было считать одинаковыми и равными соответственно ∂ξ/∂t и ∂ξ/∂x.  Выделенный объём обладает кинетической энергией ,   (24) и потенциальной энергией,  (24) где Е=ρv² – модуль Юнга, v –фазовая скорость волны (эта формула будет выведена в следующей лекции).Полная энергия. Разделим эту энергию на объём, в котором она содержится, получим плотность энергии.  (25) Подставим в это выражение уравнение волны (7.а)и приняв во внимание, что получим:(26) В случае поперечной волны для плотности энергии получается такое же выражение.         Из выражения (26) следует, что плотность энергии в каждый момент времени в различных точках пространства различна. В одной и той же точке плотность энергии изменяется со временем по закону квадрата синуса. Среднее значение квадрата синуса равно ½. Соответственно среднее по времени  значение плотности энергии в каждой точке среды равно. (27)

Замечание. Подобная зависимость имеет место и для других видов волн: сферической, цилиндрической, затухающей. Энергия доставляется от источника колебаний в различные точки среды самой волной, следовательно, волна переносит с собой энергию. Количество энергии, переносимое волной  через некоторую поверхность в единицу времени, называется потоком энергии через эту поверхность: . (28)Для характеристики течения энергии в разных точках пространства вводится понятиеплотности потока энергии:     . (29) Направление вектора плотности потока энергии совпадает с направлением переноса энергии через перпендикулярную к переносу площадку. Пусть через площадкупереносится за время ∆t энергия ∆W, заключенная в объёме цилиндра  с основанием и высотойv∆t. Если размеры цилиндра достаточно малы для того, что бы во всех его точках считать плотность энергии одинаковой, то .    (30)Подставив в (29) получим.  (31) Так как направление переноса энергии совпадает с направлением волны, то можно записать в векторном виде:.  (31.1) Этотвектор плотности потока энергии  называется вектором Умова.    Среднее значение вектора Умова равно: . (32) Это выражение справедливо для волны любого типа.

Интенсивность волны-среднее по времени значение плотности потока энергии, переносимой волной.

Полный поток энергии через некоторую поверхность равен: , (33) а его среднее значение .  (33.1) В случае плоской затухающей волны амплитуда убывает по закону

. Соответственно средняя плотность потока энергии убывает по закону . Величина2γ – называется коэффициентом поглощения волны.

Эффект Доплера для звуковых волн.Пусть источник, находящийся в газе или жидкости, испу­скает короткие импульсы c частотой v. Если источник и прием­ник покоятся относительно среды, в которой распространяет­ся волна, то частота воспринимаемых приемником импульсов будет равна частоте v источника. Если же источник, или при­емник, или оба движутся относительно среды, то частота v', воспринимаемая приемником, вообще говоря, оказывается от­личной от частоты источника: v' ≠ v. Это явление называют эф­фектом Доплера.

Сначала рассмотрим случай, когда источник S и приемник P движутся вдоль проходящей через них прямой c постоянными скоростями и и u' соответственно (относительно среды).

Если бы двигался только источник навстречу приемнику, испуская импульсы c периодом Т = l/v, то за это время очеред­ной импульс пройдет относительно сре­ды расстояние λ = υΤ, где υ - скорость волн в среде, и пока будет испущен сле­дующий импульс, источник «нагонит» предыдущий импульс на расстояние uT. Таким образом, расстояние между им­пульсами в среде станет равным λ' =υT-uT (рис. 1.11), и воспринимаемая неподвижным приемником частота (число импульсов за единицу времени) v'=υ/ λ'= υ / (T(υ-u)) (1.63)

Если же движется и приемник (пусть тоже навстречу источни­ку, то импульсы относительно приемника будут иметь скорость υ + u', и число воспринимаемых за единицу времени импульсов

v' = (υ + u') / (T(υ-u))= v (υ + u') / (υ-u) (1.65)

Принцип суперпозиции волн.

Вектор Умова.

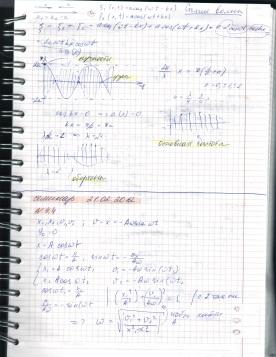
Изотропная среда – та область пространства, физические свойства которой не зависят от направления. Электромагнитные волны – распространяемые в пространстве возмущения электромагнитного поля.

Есть провод с током -> «вихревое магнитное поле», ε_i=-dφ/dt - «вихревое электрическое поле». Меняем направление электрического поля Е – возникает магнитное поле => «электрическая волна». Индекс электрического поля D=ε₀εE; B=μ₀μH – индукция магнитного поля. (μ – относительная магнитная проницаемость, μ₀ - магнитная постоянная) Е перпендикулярно Н.

Волновое уравнение (без вывода)

[ ]

Скорость электромаг. волны: 1/v²==>v=1/

Скорость электромагнитных колебаний в вакууме: C=1/ ; скорость света в вакууме: v=C/; – показатель преломления среды.