
Все билеты по ТФКП
.docx|
1. Предел последовательности комплексных чисел. Теорема о связи предела последовательности комплексных чисел с последовательностями действительных чисел. Опр1. Окресностью(ε-окр) точки Z0ÎС, наз. круг |z-z0|<ε. U(z0,ε) – окр. т.z0 радиуса ε. Опр2. Окр-тью (R-окр) т.z=∞Î Č наз. мн-во всех точек zÎČ для которых |z|>R, 0≤R<+∞. Обозн. U(∞,R). Опр3. Пусть {zn}послед чисел zn=xn+iynÎC. Число z0=x0+iy0, z0¹∞, наз-ся пределом послед-ти zn при n®∞, если: "ε>0 $N(ε): "n≥N: |zn-z0|<ε. lim(zn)=z0 при n®∞, lim(zn)=0 при n®∞. Опр4. ∞ есть предел послед-ти {zn}, если "R>0 $N(R):"n≥N |zn|>R. Теор1. Сущ-е предела lim(zn)=z0=x0+iy0 при n®∞ (1) эквив-но сущ-ю двух пределов lim(xn)=x0 при n®∞ lim(yn)=y0 при n®∞ (2). Док-во: Пусть выполн. (1). Тогда |xn-x0|<|zn-z0|, |yn-y0|≤|zn-z0|, |xn-x0|≤[(xn-x0)2+(yn-y0)2]1/2=|zn-z0|. Если выполн. "n≥N: |zn-z0|<ε, то "n≥N: |xn-x0|<ε1, |yn-y0|<ε2 => выполн усл-е (2). Обратно из (2)=>(1), т.к. |zn-z0| =[(xn-x0)2+(yn-y0)2]1/2, |xn-x0|<ε1, |yn-y0|<ε2. Пусть ε=max(ε1,ε2), то |zn-z0|<[ε2+ε2]1/2=εÖ2.■ Замеч: Из Т1 =>, что теория пределов последовательностей действ. чисел может быть перенесена на компл. числа. В частности имеет место Т2 Критерий Коши: Для того, чтобы {zn} имела конечн. предел (была сходящ) необх. и дост., чтобы "ε>0 $N(ε): "n≥N и"m≥N: |zn-zm|<ε. Или "pÎN: |zn+p-zn|<ε. |
|
|
2. Предел функции. Теорема о связи предела функции комплексного переменного с пределами функций действительного переменного. Непрерывность. Равномерная непрерывность. Функции компл. переменного. Опр. Закон f-1 по котор. " образу wÎEw ставится в соотв-е одно или несколько его прообразов zÎЕz наз-ся ф-цией z=f-1(w) обратной по отнош. к w=f(z). Замеч: Re[f(z)]=Re[f(x+iy)]=U(x,y); Im[f(z)]=V(x,y). Т.о. w=f(z)=U(x,y)+iV(x,y). Задание f(z) равносильно заданию двух ф-ций от двух действ. переменных U(x,y) и V(x,y). Предел функции, непрерывность. Опр1.(Коши) Пусть w=f(z) задана на EzÎCz и z0 – предельная точка этого мн-ва. а) Число w0≠∞ наз. пределом ф-ции f при z→z0, если "ε>0 $δ(ε)>0: "zÎEz: 0<|z-z0|<δ=>|f(z)-w0|<ε. lim(f(z))=w0 при z→z0. б) ∞ есть предел f(z) при z→∞, если "ε>0 $δ(ε)>0: "zÎEz: |z|>δ=>|f(z)|>ε. lim(f(z))=∞ при z→∞. Опр (Гейне) Число w0≠∞ есть предел f(z) при z→z0, если "{zn}:("n: zn≠z0;znÎE;z→z0): {f(zn)}→w0.
|
2. Замеч. Опред. пределов по Коши и по Гейне эквив-ны. Без док-ва!■ Тh3(эквивалентности). Сущ-е предела (при z→z0) lim(f(z))=w0=a+ib эквивалентно сущ-ю limU(x,y)=a (при x→x0, y→y0); и limV(x,y)=b (при x→x0, y→y0), где z0=x0+iy0; f(z)=U(x,y)+iV(x,y). Док-во: аналогичн. соотв. Т о послед. пределов.■ Т.о. св-ва пределов ф-ций действ. перем. переносятся на св-ва пределов ф-ций комплексн.перем. Опр2. Ф-ция f(z), опред. на E непр. в z0ÎE, если: 1) f(z) определена в некот. окрестн. т.z0, 2) сущ-ет lim(f(z)) (при z→z0), 3) lim(f(z))=f(z0) (при z→z0). Опр3. Ф-ция наз-ся непрерывн. на мн-ве E, если она непр. в " точке E. Равномерная непрерывность. Опр4. f(z) наз-ся равномерно непр. на мн-ве E, если: "ε>0 $δ>0: "z'ÎE и "z''ÎE: |z'-z''|<δ=>|f(z')- f(z'')|<ε. Тh Кантора: Ф-ция, непр. на замкн. мн-ве, равномерно непр. на этом мн-ве. Док-во: Следует из Th действит. анализа и из Th3.
|
|
3.Производная ФКП. Дифференцируемость и дифференциал. Критерий дифференцируемости. Производные Пусть ф-ция w=f(z) опред. на некот. открыт. мн-ве DÎC с предельн. точкой z0ÎD. Если $ lim((f(z0+Δz)-f(z0))/Δz) (при Δz→0) (1) при произвольн. стремлении Δz к нулю, то этот предел наз-ся производной ф-ции f в т.z0. Обозн: f '(z0); df(z)/dz |z=z0. При этом ф-ция f наз-ся моногенной в т.z0. Дифференцируемость и дифференциал. Пусть однозначная ф-ция опред-на на мн-ве DÎC и т. z0ÎD предельная точка. Ф-ция f (w=f(z)) наз. диф-мой в т.z0, если её приращение в т.z0 можно представить в виде Δw=Δf(z0)=f(z0+Δz) – f(z0)=AΔz+α(z0, Δz) (2), где A=A(z0)=const.; α(z0, Δz)=о(|Δz|),т.е. lim(α(z0, Δz)/Δz)=0 (при Δz→0). (3); Δz=Δx+iΔy; |Δz|=[Δx2+Δy2]1/2. Опр. Главн. лин. относит. Δz часть приращ. ф-ции w=f(z) в т.z0 наз. диф-лом ф-ции f в т.z0 и обозн. символом df(z0) или dw=df(z0)=A(z0)Δz (4). Тh. Для того, чтобы ф-ция f была диф-ма в т.z0 необх. и дост., чтобы она была моногенной. Док-во: 1)Необх. Пусть w=f(z) диф-ма в т.z0. Тогда Δw=AΔz+о(|Δz|). След-но (при Δz→0) lim(Δw/Δz)=A+(о(|Δz|)/Δz)=A=f '(z0).
|
3. 2) Дост. Пусть f(z)=w моногенна в т.z0. Тогда по опред. моногенности (f(z0+Δz)-f(z0))/Δz=A+β(z0+Δz). Отсюда получим: (5) f(z0+Δz)=AΔz+β(z0,Δz)Δz. (β(z0,Δz)Δz=о(|Δz|) при Δz→0). Это означ, что f диф-ма в т.z0.■ Замеч: 1) Из соотн (5) следует, что в случае моногенности ф-ции f в т.z0, f явл. непр. в этой точке (т.к. Δf→0 при Δz→0). Обратное неверно. 2) Из этой Th следует, что df(z0)=f '(z0)Δz. 3) Ф-ция f(z)=z моногенна всюду на C, т.к. f '(z)=lim(Δz/Δz)=1 при Δz→0. 4) dz=1·Δz => dz=Δz; df(z0)=f '(z0)dz (6); f '(z0)=df(z0)/dz
|
|
4. Условия Коши-Римана (C-R). Необходимые и достаточные условия моногенности(диф-ти) ФКП. Определение аналитической функции в области и в точке. Th. Пусть f(z)=w=U(x,y)+iV(x,y) опред. в нек. окр-ти и в самой т.z0. Для того, чтобы эта ф-ция была диф-ма в т.z0, необх. и дост. чтобы ф-ции U и V были диф-мы в т.z0=(x0,y0) и чтобы в этой точке выполнялось условие Коши-Римана(C-R) (1): { ∂U/∂x=∂V/∂y; ∂U/∂y=-∂V/∂x. Док-во: 1) Необх. Пусть ф-ция f диф-ма в т.z0. Тогда Δf(z0)=ΔU+iΔV=f '(z0)Δz+ō(Δz). Пусть f '(z0)=B+iC, а ō(Δz)=ō1(Δz)+iō2(Δz), B,CÎR; ō1(Δz),ō2(Δz) – функ.действ. переменных б.м. Тогда ΔU+iΔV=(B+iC)(Δx+iΔy)+ō1+iō2 (2) (3) { ΔU=BΔx+CΔy+ō1; ΔV=CΔx+BΔy+ō2. Это означ., что ф-ции U и V диф-мы в т.z0=(x0,y0). Из рав-в (3) вытекает, что (4) {B=∂U/∂x=∂V/∂y; C=-∂U/∂y=∂V/∂x. Т.о. выполн. усл-я C-R(1). 2) Дост. Пусть U и V диф-мы в (x0,y0) и выполн. (1). Тогда справедл. рав-ва (3). След-но справедл. соотн. (2). Это означает, что Δf(z0)=(B+iC)Δz+ō1+iō2. Это означ, что w – диф-ма в т.z0=(x0,y0).■ Замеч: 1) В частн. усл-я Th выполн., если ф-ции U и V имеют непр.
|
4. частн. произв. в (x0,y0) и выполн. усл-е C-R. 2) Если ф-ция диф-ма, то произв. можно считать по любому направлению. Если Δz=( Δx,0) Δw/Δz=(Δu+iΔv)/ Δx= Δu/Δx+i(Δv/Δx) -> ∂u/∂x+i(∂v/∂x)= f '(z0); Если Δz=( 0, Δy) Δw/Δz=(Δu+iΔv)/ iΔy= -i(Δu/Δy)+(Δv/Δy) -> -i(∂u/∂y)+∂v/∂y= f '(z0) 3) Если z=r·eiφ {x=r·cosφ; y=r·sinφ. f(z)=U(r,φ)+iV(r,φ). (4)(C-R) { ∂U/∂r=∂V/(r·∂φ); ∂U/(r·∂φ) =-∂V/∂r. Аналитические ф-ции. Если w=f(z) однозн. в обл. D и диф-ма в этой обл., то она наз-ся аналитичн. в этой области, а также регулярной и голоморфной. Понатие ф-ции, аналитичн. в точке. Говорят, что ф-ция f(z) аналитичн. в т.z0, если она аналитична в некот. окр-ти этой точки. Замеч: Условия диф-ти и аналитичности ф-ции f(z) в области совпадают, однако усл-я аналитичности в точке содержат больше требований, чем усл-я диф-ти. Замеч: 1) Ф-ция w(z)=U(x,y)+iV(x,y) аналитичн. в обл. D <=> когда: а) Ф-ции U и V диф-мы в обл-ти D. б) Выполн. условие C-R 2) Если ф-ции f(z) и φ(z) – аналит. в обл-ти D, то также в этой области аналит-ны ф-ции: f ± φ; φ·f; f/φ (φ≠0). 3) Если w=f(z) аналит. в обл. D и w=φ(w) аналит. в обл. D и имеет смысл сложная ф-ция w=φ(f(z)) опр. в обл. D, то эта ф-ция аналит. в обл. D, что следует из того, что w'z= φ'(w)·f '(z). |
|
5. Геометрический смысл аргумента производной. Пусть задана гладкая кривая Жордана γ, кот. опред. соотн. z=x(t)+iy(t), α≤t≤β. γ: {x=x(t); y=y(t). α≤t≤β. Причем z0Îγ; z0=z(t0), t0Î(α,β). z0 – внутр. точка этой кривой. Т.к. дуга гладкая, то z'(t0)≠0. {есть рис.} Пусть задано отобр. w=f(z) и пусть Г - образ γ при этом отображении. Мы также потребуем, чтобы отобр. f было аналитично в т.z0. и f '(z0)≠0. Тогда Г будет иметь вид: w=f(z(t)) и w'= f '(z0)·z'(t)≠0. (1) Из ф-лы (1) видно, что Г имеет касат. в т.w0=f(z0). Т.к. при перемножении ФКП аргументы складываются, то из (1) следует, что arg(w'(t0))=arg(f '(z0))+arg(z'(t0)); arg(f '(z0))=arg(w'(t0))- arg(z'(t0)) (2) q=y-j. Здесь q - угол поворота дуги γ в т.z0 при отображ. w=f(z). Отсюда вытекает след. геом. смысл производной: Аргумент производной f '(z0) равен углу поворота дуги γ в т.z0 при отображ. w=f(z). Пусть теперь γ1 – некот. гладкая кривая Жордана, не совпад. с γ, а Г1 – образ γ1. Пусть отображение – то же самое.
|
5. Тогда согласно (2): arg(f '(z0))=arg(w1'(t0))-arg(z1'(t0)) (3) и согласно (2) и (3) имеем: arg(w'(t0))-arg(z'(t0))=arg(w1'(t0))-arg(z1'(t0)) (4). Соотн. (4) означает, что угол между дугами γ и γ1 в т.z0 – т. пересеч. γ и γ1 – равен углу между их образами Г и Г1 в т.w0. Если f(z) – аналитична в нек. окр-ти т.z0. и f '(z0)≠0, то при отображении w=f(z) имеет место закон сохранения углов между кривыми, проходящими через т.z0, как по величине, так и по направлению их отсчета. Геометрический смысл модуля производной Рассм. те же условия и кривые: (Вопрос 5) | d z0| = [ [x’(t0)]2 + [y’(t0)]2 ]1/2 dt = ds0, | d w0| = [ [U’(t0)]2 + [V’(t0)]2 ]1/2 dt = dS0. | f ’(z0)| = (|dw/dz|) |z= z0 = (d S0)/(d s0) (5) ǽ= (d S0)/(d s0) - есть коэф.-нт лин. растяж. дуги γ в т. z0 при отображ. w = f(z). т. е. геом. смысл модуля производной заключен в том, что |f ‘(z0)| = коэф.-нту лин. растяж. дуги в т. z0 при задан. отобр. Это локальн. коэф. растяж. и он не зависит от направления.
|
|
6. Конформное отображение Опр. Непр. в некот. окр. т. z0 отображ. w =f(z) наз. конформным, если оно сохраняет углы между кривыми, проход. через эту точку и локальн. коэф-нт ǽ в т. z0 одинаков по всем напрвл. Опр. Отобр. конформно в обл. если оно конформно в кажд. т. этой обл-ти. Замеч. Из предыдущ. след., что если ф-ция анал. в т. z0 и f ’(z0) ≠0, то f(z) – конформно отобр. нек. окр. т. z0. Основные теоремы теории конформных отображений Тh1. О сохранении области Если ф-ция w =f(z) – аналитична в однолистна в области D, то f ’(z) ≠0 в обл. D, и w =f(z) – кон-формно отобр. некот. обл. D на G, Причем обратн. ф-ция Z=f -1 (ω) аналитич. в области G.
|
6. Тh2. Римана. Пусть граница односвязн. области D Э Cz сост. более, чем из 1 точки тогда существ. аналит. функции., которые отобр. обл. D на внутренность единичн. круга, причем только 1-на из этих ф-ий переводит задан. т. z0 Э D и выходящее из нее задан. направление в задан. точку w0 и выходящ. из нее задан. напрвление. Th3. О соответствии границ. Пусть D и G – две обл.-ти, огранич. замкнт. кривыми Жордана ∂D; ∂G соответственно. Если ф-ия f комформно отображ. D на G , то она взаимнооднозначно и непрерывн. отобр. обл-ть D* = D U ∂D ; G* = G U ∂G; с сохран. напрвл. обхода границ.
|
|
7. Линейные отображения w=a*z+b , a≠0, a,b Э C (1) w’=( a*z+b) ’=a ≠ 0. a = α1 + i*α2 b = β1 + i*β2. U + i*V = (α1 + i*α2)(x + i*y) + β1 + i* β2 { U = α1x + β1 – α2*y ; V = α2*x + β2 + α1*y. J = | (Ux)’, (Uy)’; (Vx)’, (Vy)’ | = | α1, - α2; α2 , α1| = α12 + α22 = | α1 + i*α2 |2 = |a|2 ≠ 0 Следн-но это отображ. конформное . Рассм. обр. отображ. z = (w-b)/a = (1/a) w – b/a ; a ≠0. Данное отображ.(прямое и обратное) конформно на С (рассматриваемая комплексная плоскость). Понятии конформ. в т. z = ∞ Опр. Однолистное в окр. т. z = ∞ отображ. w =f(z) конформно в т. z = ∞, если при замене z = 1/ξ отображ. w=f(1/ξ) = φ(ξ) конформно в т. ξ=0 Проверим конформность лин. отображ. в т. z = ∞. z = 1/ξ , ω=1/η, тогда в окр. z = ∞ и ее образ w = ∞ → ξ=0; η=0. η= ξ/(a+b*ξ) , η’=a/(a+b*ξ)2 , (η’ | ξ=0) = 1/a ≠0 Отобр. (1) w=a*z+b можно предств. a = |a|eiӨ (2) ;z=reiγ ; az = |a|eiӨ reiγ w1-это отображение подобия с центром в точке z=0. w2= exp(i *arg(a)) w1 (3) - это вращ. вокруг точки w=0 на угол arg(a) w = b+ w2 – парал. перенос.
|
8. Дробно-линейные отображения и его свойства w=(a*z+b)/(c*z+d) , a/c≠b/d (8) a, b, c, d Э C, c≠0, то это отображение можно преобразовать к виду: w=A+B(1/z+ z0) (9) , A, B, z0 Э C Дробн.- лин. отобр. свод. к след. 3-м суперпозиц.: 1)w1=z+ z0 – парал. сдвиг (10) 2) w2=1/w1 – инверсия отн. окр. радиуса 1 (11) 3) w=A+Bw2 – лин. отображ. (12) Исходя из 3-х послед. формул – Д.Л.О. окр. перев. в окружн. Св-ва Д.Л.О : 1)Из ф-л (10)-(12) непосредств. следует: а) отобр. (8) осущ. взаимноодн. отобр. плоскости С*z на C*w б) суперпоз. 2-х Д.Л.О, а также обратное отображ. явл-ся снова Д.Л.О Для док-ва суперпоз.-ии нужно подст. z=(a1z1+b1)/(c1z1+d1) и мы снова получ. Д.Л.О 2) Двойное отношение 4 точек Опр. Двойным отнош.(ангармоничным) отношением 4х точек z1,z2…z4 наз. выраж. (z1 z2 z3 z4)=[( z1- z3)/( z2- z3)]/[( z1- z4)/( z2- z4)] 3)При Д.Л.О двойное отношение 4-х попарно различн. точек не изменяется т.е. если zi→ wi с помощью Д.Л.О, то: [(w1- w3)/( w2- w3)]/[( w1- w4)/( w2- w4)] = [(z1- z3)/( z2- z3)]/[( z1- z4)/( z2- z4)] (13) Док-во: Пусть точки z1, z2, z3, z4 принадл. Сz функцией w=(a*z+b)/(c*z+d) отображаются соответственно в точки wk=(a*zk+b)/(c*zk+d) (k=1,2,3,4) Подставим в формулу (12) выражения для разности: wi-wj=(a*zi+b)/(c*zi+d) - (a*zj+b)/(c*zj+d) =[(ad-bc)(zi-zj)]/[(czi+d)(czj+d)]; i=1,2; j=3,4. После алгебраических преобразований получим правую часть формулы (12).
|
|
9. Интеграл ФКП по ориенторованной кривой и его св-ва Пусть γ – ориент. кусочно-гладк. кривая на пл-ти С с началом в т. a и c концом в т. b. Пусть L – длина γ. Пусть f(z)=U(x,y)+i*V(x,y) – огр. ф-ия, задан. в точках ZÎγ. Опр. Интегралом от ф-ии f(z) по ориентир. кривой γ наз. число, обознач. символом: òf(z)dz = ò [U(x,y)+iV(x,y)](dx+idy) = ò U(x,y)dx – V(x,y)dy + iò V(x,y)dx + U(x,y)dy (1) Из этого опр-ия следует, что для сущ. инт-ла òf(z)dz необх. и дост. сущ. 2-х криволин. инт-ов второго рода от ф-ии действ. переменного. Некоторые св-ва: 1) γ+òf(z)dz= - [γ- òf(z)dz] ( интегралы берутся по γ, далее везде) 2) òdz = b-a ; f(z)=1 òdz = òdx+iòdy = a1òb1dx + ia2òb2dy = (b1-a1) + i(b2-a2)= (b1+ib2)-(a1+ia2)=b-a. 3)Линейность интеграла ò[af(z)+bg(z)]dz= a*òf(z)dz+b*òg(z)dz 4)Аддитивность γòf(z)dz = γ1òf(z)dz+ γ2òf(z)dz , γ= γ1 U γ2 5)| òf(z)dz| ≤ ò |f(z)| |dz| = { |dz|=(dx2+dy2)1/2 = dl } =ò |f(z)|dl ≤ L max | f(z)| zÎ γ , L – длина
|
10. Теорема Коши для простого контура. Th. Если ф-я f(z) аналитична в односвязной области D, то интеграл от f(z) по " замкнутой, кусочно-гладкой кривой Жордана gÎD равен нулю: g(ò)f(z)dz=0 (1) Док-во: Мы докажем эту Th. Для случая, когда ф-я f(z)=U(x,y) + iV(x,y) имеет непрерывную производную в области D, т.е. U(x,y), V(x,y)ÎC1(D). По формуле Грина: gòP(x,y)dx + Q(x,y)dy = Dòò(¶Q/¶x - ¶P/¶y)dxdy (2) D –область огранич.кривой g; P,QÎC1(D) gòf(z)dz = gò(U + iV)(dx + idy) = gòUdx – Vdy + igòUdy + Vdx, получим: gò f(z)dz = -Dòò(¶V/¶x + ¶U/¶y)dxdy + i Dòò(¶U/¶x - ¶V/¶y)dxdy = 0 (C-R) Следствие: Пусть при условиях Th. g1 и g2 имеют общие начальные и конечные точки, так что - замкнутая кривая g1Èg2 ÎD. Тогда g1òf(z)dz =g2 òf(z)dz Это означает, что интегрирование не зависит от пути интегрирования. g1Èg2òf(z)dz = g1ò + g2- ò = 0; g1 ò f(z)dz - g2 ò f(z)dzÞ g1ò = g2ò Th. Коши(обобщённая), когда ф-я не явл. аналитической на границе(на контуре интегрирования). 1)f(z) аналитична в односвязной области D, границей которой является кусочно-гладкая кривая Жордана. 2) f(z) непрерывна в Ď=DÈg То: gòf(z)dz=0 Без док-ва.
|
|
11. Интегральная формула Коши. Th. Пусть граница ¶D (n+1)-связной области D состоит из спрямляемых взаимно непересекающ. кус.-гл. замкнутых кривых Жордана, причём С1…Cn расположены внутри С0. Тогда если f(z) – аналитическая ф-я в обл. D и непр. в замкнут. обл. Ď=DȶD, то справедлива формула: [1/2pi]
* ¶Dò[f(x)
/ (x-z)]dx
= {f(z),
zÎD;
0, zÏĎ}
(1)
где интегрирование производится в положительном направлении, т.е. область при обходе границы остается слева, т.е. ¶D= С0ÈČ1È Č 2È…ÈČ n Док-во: Пусть
zÎD.
Зафиксируем в обл. D
т.z
и круг U(z,r)
с центром в z – имеет границу g
и радиус r. Зафиксируем круг т.о., чтобы
он вместе с границей не пересек. границу
¶D.
|
11.
Тогда
по обобщенной Th.Коши:
¶D*ò[f(x)
/ (x-z)]dx
= ¶Dò[f(x)
/ (x-z)]dx
+ g-ò[f(x)
/ (x-z)]dx
= 0
Отсюда, т.к. выполняется g -ò = - gò , получим: ¶Dò[f(x) / (x-z)]dx = gò[f(x) / (x-z)]dx (2) . Ранее вычислили: gò[ dx/ (x-z)] = 2pi(3) Отсюда f(z) можно предствить в виде: f(z) = [1/2pi]*f(z)*2pi = [1/2pi]* f(z)* gò[ dx/ (x-z)] = [1/2pi]* gò[f(z)/(x-z)]dx (4) На основании (2) и (4) имеем: f(z) - [1/2pi] * ¶Dò[f(x) / (x-z)]dx = [1/2pi] * gò[ (f(z) - f(x)) / (x-z)]dx (5) Т.к. f(x) непр. в т.z, то" ε>0 $d(e): при r<d ½f(z) - f(x)½< e Тогда из формулы (5) имеем: ½f(z) - [1/2pi] * ¶Dò[f(x) / (x-z)]dx ½< [1/2pi]*½gò[ (|f(z) - f(x)|) / (|x-z|)] |dx|½= [1/2pi]* e*2pi = e |
|
12. Интеграл типа Коши. Существование производных всех порядков у аналитической функции. Опр. Пусть Г- кус.-гл. кривая Жордана, а f(x)- непр. ф-я, заданная на Г. Пусть zÎС, zÏГ. Тогда ф-я F(z)= [1/2pi] * Гò[f(x) / (x-z)]dx (1) наз. интегралом типа Коши. Если Г-замкнута, а f(x) – аналитична в огр. обл. D с границей Г и непр. в замкн. обл. Ď=DÈГ,то интегр. (1) - интеграл Коши и имеет место рав-во: F(z)={f(z), zÎD; 0, zÏ Ď=DȶD} (2) Th.
Ф-я, определяемая интегр. типа Коши
F(z)=
[1/2pi]
* Гò[f(x)
/ (x-z)]dx
иммет в кажд. т. zÏГ
производные всех порядков, кот. вычисл.
по ф-ле: F(n)(z)=
n!/
[2pi]
* Гò[f(x)
/ (x-z)n+1]dx
(3)
Док-во: Выведем формулу (3) для n=1. Зафиксируем произв. т.zÏГ. Пусть d - расстояние от z до Г. d=ρ(Г,z) = inf|z-x|;xÎ Г; zÎ (z, d/2). Рассм. круг с центром в т.z и радиуса d/2. Тогда " т. z+DzÎ U(z,d/2) (Dz≠0) имеем: ½x-z½>d/2 и½x-z-Dz ½>d/2. Рассмотрим отношение: [F(z+Dz) – F(z)]/ Dz = [1/2pi] * (Гò[f(x) / (x-z-Dz)] - Гò[f(x) / (x-z)])*[1/ Dz] dx = [1/2pi] * Гò[f(x) / ((x-z)* (x-z-Dz))]dx (4) т.к. "xÎГ: ½x-z½>d/2,½x-z-Dz ½>d/2. Из (4) имеем: |
12.½[F(z+Dz) – F(z)]/ Dz - [1/2pi] * Гò[f(x) / (x-z)2]dx ½ = = [1/2pi]*½ Гò[(f(x)*Dz) / ((x-z)2* (x-z-Dz))]dx ½< <[1/2p]*Гò[(½f(x)½*½Dz½*½dx½)/(½x-z½2*½x-z-Dz½)]
<(M*½Dz½*L)/(2p*(d/2)3)
L – длина кривой; M=maxxÎ Г½f(x)½; (5)®0 при ½Dz½® 0, след-но $ предел: limDz->0 ([F(z+Dz) – F(z)]/ Dz) = [1/2pi] * Гò[f(x) / (x-z)2]dx =F’(z) Пользуясь методом мат. индукции и ф-лой (6) устанавливается справедливость ф-лы (3) для n=2,3,… Следствие($е производной "порядка у аналит. ф-ции): Если ф-я аналитич. в обл. D, то она имеет производн. " порядка в этой обл. Док-во: Пусть z – произв. т. обл. D, а U(z,r) – окр-сть(круг) с границей g и радиуса r с центром в z. Круг Î обл. D. Тогда по интегр. формуле Коши: f(z)= [1/2pi] * gò[f(x) / (x-z)]dx, где zÎU(z,r). Это интеграл типа Коши Þ ф-я имеет производн. " пор-ка в т.z . Т.к. z-произв. т. обл. D, то и во всей обл. Отсюда также следует, что "n : f(n)(z) аналитична в D. |
|
13. Первообразная. Достаточные условия $я первообразной. Опр. Пусть ф-я f(z) определена в D. Аналитич. в этой обл. F(z) наз. первообразной для f(z), если в D, если: F’(z)=f(z). Очевидно, что F(z)+C, C=const, также явл-ся первообр. для f(z). Th. Если F(z) и Ф(z) – первообр. в D для f(z), то Const= F(z) - Ф(z) Док-во: Пусть W(z)= F(z) - Ф(z). Тогда dW(z)/dz = F’(z) – Ф’(z) = f(z)- f(z)=0. Пусть W(z) = U(x,y) + iV(x,y) Тогда dW(z)/dz = ¶U/¶x + i¶V/¶x = ¶V/¶y - i¶U/¶y = 0 Þ ¶U/¶x = 0; ¶V/¶x = 0; ¶V/¶y = 0; ¶U/¶y = 0; Откуда следует, что U(x,y)=const; V(x,y)=const; Þ W(z) = const. Достаточные усл-я $ первообр.: Th. Пусть: 1.Ф-я f(z) непр. в односвязной, огр. обл D 2."
замкн. кус-гл. кривой Жордана CÎ
D:
Тогда: 1)"т.aÎD,
"zÎD:
F(z)
=
2)"zÎD $ производная F’(z) = d\dz [C òf(x)dx] = f(z) (2), F(z) – первообр. f(z).
|
13. Док-во: Согласно 2-ому усл-ю Th. aòzf(x)dx не зависит от пути, соедин. точки a и z. Пусть точка z и Dz (Dz¹0) Î некот. окрестности т.z U(z)Î D. Тогда [F(z+Dz) – F(z)]/ Dz = [1/Dz]*( aòz+Dz f(x)dx - zòaf(x)dx)=[1/Dz]* aòz+Dz f(x)dx (3) Вследствие незав-сти интеграла от пути будем считать g - отрезком прямой. Т.к. f(z) – непр. в D и в окр. U(z), то "xÎU(z), f(x)=f(z)+h(x) (4), где h(x)®0 при x®z (5). Т.к.путь, соедин. z и z+Dz – есть отрезок прямой, то:{zòz+Dz ½ dx½=½Dz½ и zòz+Dz f(x)dx = f(z) Dz (6) Так же ½[1/Dz]* zòz+Dz h(x)dx½£ [1/½Dz½]*maxxÎ g½h(x)½* zòz+Dz ½dx½=max xÎ g ½h(x)½ Из этой оценки и на основании (5): limDz->0[1/Dz]* zòz+Dz h(x)dx=0 (7) На основании (4),(5),(6) для правой части (3) имеем: lim [1/Dz]*zòz+Dz f(x)dx = lim{ [1/Dz]* zòz+Dz [f(z) + h(x)]dx} = = lim{ [1/Dz]* zòz+Dz f(z)dx + [1/Dz]* zòz+Dz h(x)dx]} = f(z) при Dz®0 (8) Переходя к пределу в (3) при Dz®0 , учитывая (8): F’(z) = d\dz [aòzf(x)dx] = f(z) (9)
|
|
14. Формула Ньютона-Лейбница. Теорема Морера(достаточные усл-я аналитичности ФКП в области). Всё это следствия из Th. и её следствия: Достаточные усл-я $ первообр.: Th. Пусть: 1.Ф-я f(z) непр. в односвязной, огр. обл D 2."
замкн. кус-гл. кривой Жордана CÎ
D:
Тогда: 1)"т.aÎD,
"zÎD:
F(z)
=
2)"zÎD $ производная F’(z) = d\dz [C òf(x)dx] = f(z) (2), F(z) – первообр. f(z). Следствие1: Если ф-я f(z)- аналитич. в огр. односвяз. D,то " числа а и " zÎ D ф-я F(z) = aòzf(x)dx явл-ся аналитич. в D и первообр. для ф-ции f(z).
|
14. Следствие 2(Ф-ла Ньютона-Лейбница). Если ф-я f(z) аналитична в огр. односвязн. обл. D , а Ф(z) - какя-нибудь её первообразная в этой обл., то "z1,z2ÎD справедлива ф-ла Н-Л: z1òz2f(z)dz = Ф(z2) - Ф(z1) Док-во: Если Ф(z) - первообразная, то Ф(z)= z1òz2f(x)dx + С, но Ф(z1)= z1ò z1f(x)dx + С = С, поэтому Ф(z2)= z2ò z2f(x)dx + Ф(z1), откуда и следует ф-ла Н-Л. Th. Морера. Если ф-я f(z) – непр. в односв. обл. D и " спрямл. замкн. кус-гл. кривой
Жордана СÎ
D
:
Док-во: Согласно Th(Следствию 1) при сделанных предположениях ф-я f(z)= d/dz[F(z)] = d/dz[aòzf(x)dx], aÎ D. Т.о. f(z) имеет аналитическую первообразную в обл. D, т.е. F’(z)=f(z) "zÎD. Тогда согласно $ю производной " порядка у аналитич. ф-ции заключаем, что f(z)-аналитическая ф-я.
|
|
15. Функциональные ряды. Достаточные услолвия равномерной сходимости (признак Виерштрасса). k=1∑∞ fk(z) (1) Опр. Ряд (1), где fk(z) – однозначные ф-ции от z, заданные на некотором мн-ве ЕЄС, наз. Функциональным рядом (ф.р.). Sn(z)= k=1∑n fk(z) (2)-частичная сумма ряда (1)ю Опр1. Ряд (1) сходится в т. z0ЄЕ, если сходится ряд k=1∑∞ fk(z0). Ряд (1) сход на мн-ве Е , если он сход в каждой точке Е. В этом случае его сумма – есть однозначная ф-ция на Е: f(z) = k=1∑∞ fk(z). Опр2. Ряд (1) наз равномерно сход-ся на Е, если : 1) для " ε >0 $ N(ε) : " n≥N и " zÎE: |f(z)-Sn(z)|=| k=1∑∞ fk(z)| < ε . 2) " ε >0 $ N(ε) : " n≥N и " zÎE: supzÎЕ|Rn(z)|< ε, или limn→∞(supzÎ Е|Rn(z)|)=0. 3) " ε >0 $ N(ε) : " n≥N, " pÎ N и " zÎE:| k=n+1∑n+p fk(z)| < ε Th(дост усл равн сход-ти или призн вейерштрасса) Если числовой ряд k=1∑∞ αк , где для "к: αкÎR и αк ≥0, сходится, и для "к и " zÎE: |fk(z)| ≤αк , то ряд (1) сход-ся равномерно на Е. Док-во: т.к. ряд k=1∑∞ αк сход-ся , то для него выполн. Крит Коши: " ε >0 $ N(ε) " n≥N и " pÎN: k=n+1∑n+p αк <ε. Тогда для "к и "zÎE: |k=n+1∑n+p fk(z)|≤ k=n+1∑n+p |fk(z)|≤ k=1∑∞ αк <ε .
|
16. Достаточные условия непрерывности функциональнонго ряда. k=1∑∞ fk(z) (1) Th. Если ряд (1) сх-ся равномерно на мн-ве Е к ф-ции f(z), и все его члены fk(z) – непрерывные ф-ции на Е, то и f(z) непр-на на Е. Док-во: пусть z0– произвольная точка Е. Т.к. ряд (1) сход. равн-но , то " ε >0 $ N(ε) : " n≥N и " zÎE: |f(z)-Sn(z)|< (ε /3) (2) . Т.к. SN(z)– непр-на на Е, то для нашего ε >0 $ δ=δ(ε , z0), что "zÎE: при |z - z0|<δ : | SN(z) – SN(z0)|<(ε/3). Тогда " z : |z - z0|<δ , zÎE : |f(z)-f(z0)|=|f(z)- SN(z)+SN(z)-SN(z0)+SN(z0)-f(z0)|≤|f(z)- SN(z)|+|SN(z)-SN(z0)| + |SN(z0)-f(z0)|<(ε/3)+(ε/3)+(ε/3)=ε . # {здесь |f(z)- SN(z)|<(ε/3) и |SN(z0)-f(z0)|<(ε/3) из-за равномерной сходимости Опр2. Ряд (1) наз равномерно сход-ся на Е, если : 1) для " ε >0 $ N(ε) : " n≥N и " zÎE: |f(z)-fn(z)|=| k=1∑∞ fk(z)- k=1∑n fk(z)|=| k=n+1∑∞ fk(z)| < ε . 2) " ε >0 $ N(ε) : " n≥N и " zÎE: supzÎЕ|Rn(z)|< ε, или limn→∞(supzÎЕ|Rn(z)|)=0. {1) и 2) разные формы записи одного и того же}}
|
|
17. Степенные ряды, круг и радиус сходимости. Теорема Коши-Адамара. Степ. рядом наз. ряд вида: k=0∑∞ ck * (z- z0) k , где ck и z0 -комплексные числа (const) и постоянные, а z – комплексная переменная. k=0∑∞ ck * z k (1) Опр.Число R наз. радиусом сход-ти ряда (1), а |z|<R наз. кругом сход-ти ряда (1). Замеч. Радиус мы так же можем определить на основании признака Даламбера: R= k→∞lim (|ck/ck+1|) = k→∞lim (|ck|/|ck+1|). Th Коши –Адамара: Пусть
дан ряд (1). Рассмотрим предел: L
= k→∞ Док-во: k→∞ Если |z|<R, то q<1 , сл-но ряд сход. Если |z|>R, то q>1, сл-но расх. |
|
|
18. Степенные ряды. Первая теорема Абеля. Теорема Абеля о равномерной сходимости степенного ряда. Аналитичность суммы степенного ряда внутри круга сходимости. Степенным рядом наз. ряд вида: k=0å¥Ck(z-z0)k (1), где Ck и z0 - комплексные числа (const), а z - комплексная переменная. k=0å¥Ckzk (1) z0 – в начале координат. Th (1ая теорема Абеля): Если ряд (1) сх-ся в точке z0¹0, то он абсолютно сх-ся в круге |z|<|z0|. Док-во: Т.к. ряд (1) сх-ся в точке z0¹0, то из Th Коши-Адамара |z0|£R, где R – радиус сх-ти ряда. Значит и для круга |z|<|z0|<R выполняется условие абс. сх-ти. # Th (Абеля о равномерной сход степенного ряда): Ряд (1) сходится равномерно в " замкнутом круге |z|≤r, если этот ряд имеет радиус сходимости R³0, а 0<r<R Док-во: Т.к. выполн. Нер-во 0<r<R, то по Th Коши-Адамара сход. ряд k=1å¥|Ck|rk. Если |z|£r, то |Ckzk|£|Ck|rk => по мажорантному признаку Вейерштрасса ряд k=1å¥|Ck|zk сх-ся равном. в круге |z|£r. # |
18. Замечание: если R=¥, то ряд сход. равном. на всей компл. пл-ти. Th(Аналитичность суммы степ. ряда внутри круга сх-ти): Сумма S(z) степ ряда (1) есть аналитическая ф-ция в его круге сх-ти |z|<R, R>0, и в этом круге ряд можно почленно дифференцировать любое число раз, причем радиус сх-ти ряда S(n)(z) = k=0(k=n+1)å¥Ck(k-1)…(k-n+1)zk-n (2) также равен R. Док-во: Все члены ряда(1) – аналитич. ф-ции в круге сх-ти, и этот ряд сх-ся равном. в данном круге Þ по Th Вейерштрасса о почленном диф-нии ряда сумма этого ряда S(z) - есть аналитич. ф-ция и ее можно диф. почленно n число раз. Th Коши –Адамара: Пусть
дан ряд (1). Рассмотрим предел: L
= k→∞ Th(дост усл равн сход-ти или призн вейерштрасса) Если числовой ряд k=1∑∞ αк , где для "к: αкÎR и αк ≥0, сходится, и для "к и " zÎE выполняется нер-во: |fk(z)| ≤αк , то ряд (1) сход-ся равномерно на Е. |
|
19. Ряд Тейлора. Теорема о разложении аналитической ф-ии в ряд Тейлора. Опр. Пусть ф-ция f(z) аналитична в U(z0,R), тогда ряд k=0å¥[[f(k)(z0)/k!]*(z-z0)k] (1) наз. рядом Тейлора от f(z) с центром разложения в точке z0. Th.
(О разложении
аналит ф-ии в ряд Тейлора).
Если ф-ция f(z)
аналит. в обл. D,
то в каждой точке z0ÎD
$
круг U(z0,R)
причем круг с границей Док-во:
Построим
круг U(z0,r)
такой, причем замкнутое мн-во этого
круга |
19. для "xÎCr Þ Выражение (2) есть сумма геометрической прогрессии 1/(x-z) = k=0å¥[(z-z0)k/(x-z0)k+1(3). Ряд справа в ф-ле(3) сход. равномер. на окружности Cr, т.к. [(z-z0)k/(x-z0)k+1]1/k=q<1. Поэтому его можно почленно интегр. Умножим обе части рав-ва(3) на f(x)/(2pi) которая ограничена на Cr. Результат проинтегрируем по контуру Cr почленно: (1/2pi)Crò[(f(x))/(x-z)]dx = k=0å¥[(1/(2pi) Crò[(f(x))/(x-z0)k+1]]dx*(z-z0)k (4) или согласно (1) можно записать: f(z) = k=0å¥[Ck*(z-z0)k] где Ck = [(1/(2pi) Crò[(f(x))/(x-z0)k+1]]dx = (f(k)(z0))/(k!) (5). # Док-во единственности: Пусть f(z) = k=0å¥[bk*(z-z0)k], тогда bk = (f(k)(z0))/(k!) (k=0,1,2,3) |
|
20. Нули аналитической функции. Порядок нуля. Теорема об изолированности нулей аналитической функции. Определение 1. Пусть ф-ция f(z)определена в обл. D, точка aD называется нулем ф-ции f, если f(a)=0. Порядок нуля. Пусть f(z) аналитична в некоторой окрестности нуля, т.е в U(a) и f(z)0. Тогда по Th Тейлора в окрестности U(a) функция f(z) представима рядом Тейлора f(z)=k=0 Ck(z-0)k (1)и этот ряд обязательно имеет отличные от нуля коэффициенты. Если в разложении (1) коэффициенты C0=C1=..=Cn-1=0 ,но Cn0 то говорят , что точка a – это нуль n–го порядка ф-ции f(z). Ясно что f(a)=0=C0. Теорема (об изолированности нулей аналитической ф-ции): Ф-ция f(z) аналитическая в окрестности U(a) своего нуля a порядка n. и f(z)0 в любой окрестности точки а (своего нуля). |
20. Тогда сущ. окрестность U1(a) , где нет никаких других нулей , кроме а и f(z) представима в виде : f(z)=(z-a)n(z), n=1,2,…, где (z) аналитическая функция и (z)0 в U1(a). Доказательство: Из условия теоремы следует, что ф-ция представима в окрестности U(a) рядом Тейлора: f(z)=Cn(z-a)n+ Cn+1(z-a)n+1+…=(z-a)n(Cn+Cn+1(z-a)+..)=(z-a)n(z), где Cn0, n≥1, (z)= Cn+Cn+1(z-a)+.. Здесь(z) аналитическая ф-ция как сумма сходящегося степенного ряда, (z) – непрерывна в U(a), т.к. Cn0 (a)0 . В следствии непрерывности (z) в точке a существует окрестность U1(a), где (z)0. т.о. функция f(z)=(z-a)n(z) не имеет других нулей , кроме а в этой окрестности. Th.
(О разложении
аналит ф-ии в ряд Тейлора).
Если ф-ция f(z)
аналит. в обл. D,
то в каждой точке z0ÎD
$
круг U(z0,R)
причем круг с границей |
|
21. Ряд Лорана. Теорема о разложимости аналитической в кольце функции в ряд Лорана. Ряды Лорана. Рядом Лорана называется ряд f(z)=k=- Ck(z- z0)k (1),Ck,z - некоторые комплексные числа ,z0 - центр ряда. Ряд(1) можно представить в виде : I(правильная часть) k=0 Ck(z-z0)k +II(главная часть) k=0 C-k/(z-z0)k. Ряд(1) сходится в точке, если в точке z сходятся ряды I и II. Сходится для I: |z-z0|R1, 0R1+ . для II k=1 C-k /(z-z0)k= k=1 C-k k, k =1/(z-z0),этот ряд сходится в некот.круге ||r , 0r+. 1/(z-z0)r |z-z0|1/r =Rr. Теорема Лорана(о разложимости аналитической в кольце функции в ряд Лорана.) Если функция f(z) аналитична в кольце k: 0r|z-z0|R=+ то она в этом кольце представима рядом Лорана: f(z)= k=-+ Ck(z-z0)k (2) где Ck=1/2i Cf()/(-z0)k+1d (3) C : |-z0|=, rR Доказательство: Пусть zk – любая точка . Очевидно существует k1: rr1|z-z0|R1R. zk1 т.к.f(z) –аналитична в кольце (включая его границы), то для точки zk1 , справедлива интегральная форма Коши f(z)=1/2i CR1(f()/(-z))d - 1/2i Cr1(f()/(-z))d (4) . Пусть CR1 , тогда |z-z0/-z0|=|z-z0|/|-z0|1 для СR, 1/(-z)=1/(-z0+z0-z)= 1/(-z0)*1/(1-(z-z0/-z0)), 1/(-z)= k=0(z-z0)k/(-z0)k+1 (5). |
21. В силу равномерной сходимости по CR1 ряда (5), его можно почленно интегрировать по окрестности CR1. Умножим обе части равенства (5) на f()/2i и проинтегрируем левую и правую части по CR1: 1/2i*CR1(f()/(-z))d=k=0(1/2i*CR1(f()/(-z0)k+1)d(z-z0)k ; 1/2iCR1(f()/(-z))d= k=0Ck(z-z0)k (6); Ck= 1/2i*CR1(f()/(-z)k+1)d (7). Рассмотрим интеграл по CR1: CR1(f()/(-z))d (8) из формулы (4). Для этого случая будет соотношение такое |(-z0)/(z-z0)|1, Cr1; 1/(-z)=1/(-z0+z0-z)*(-1/(z-z0))(1/(1-(-z0/z-z0))). Получим аналогично предыдущему : 1/2iCR1(f()/(-z))d= - k=1[1/2i*Cr1(f()/(-z0)k+1)d]1/(z-z0)k Поменяем индекс суммирования k-k получим: 1/2iCr1(f()/(-z))d= - k--1Ck(z-z0)k(9) где Сk=1/2i*Cr1f()/(-z0)k+1d(10). Подставив (6) и (9) в выражение для интегралов в формулу (4) получим представления f(z) в виде ряда Лорана: f(z)= k=0Ck(z-z0)k+ k--1Ck(z-z0)k= k=-+Ck(z-z0)k (11) , где коэффициенты Ck ((7) k0;(10) k0) . Вследствие аналитичности в кольце k функции f(z) и на основании обобщенной теоремы Коши интегралы в (7) и (10) не изменяются , если в качестве контура интегрирования взять любую окружность C: |z-z0|=, а rR произвольное число можно считать , что Ck=1/2i*C(f()/((-z0)k+1))d (12) т.к.zk есть любая точка этого кольца , то теорема доказана . |
|
22.Область равномерной сходимости ряда Лорана. Единственность разложения функции в ряд Лорана. Ряды Лорана. Рядом Лорана называется ряд f(z)=k=- Ck(z- z0)k (1),Ck,z - некоторые комплексные числа ,z0 - центр ряда. ряд Лорана: f(z)= k=0Ck(z-z0)k+ k--1Ck(z-z0)k= - k=-+Ck(z-z0)k (2) , Доказательство. Правильная часть ряда Лорана (2) есть степенной ряд , поэтому на основании теоремы Абеля он сходится равномерно в круге |z-z0|R ,01. Главная часть ряда Лорана сходится вне круга |z-z0|r следовательно сходится равномерно на множестве |z-z0|=r/ , где 01 . Итак , ряд Лорана сходится равномерно в кольце r/|z-z0|R, где 01 и где r/R. Теорема (единственность разложения в ряд Лорана) Разложение функции f(z) в ряд Лорана в кольце k: r|z-z0|R единственно. Доказательство. Пусть f(z)=k=- Ck(z-z0)k = k=- bk(z-zk)k (3). Зафиксируем любое число n=0,+-1;+-2,.. и умножим обе части равенства на (z-z0)-n-1 , полученный результат, проинтегрируем почленно по окружности |z-z0|= , что возможно согласно равномерной сходимости рядов, причем rR. Известно что интеграл |z-z0|=(z-z0)mdz={2i,m= -1;0,m-1 (4) . Используя (4) , получаем следующее 2iCn=2ibnCn=bn .Единственность доказана |
23. Выражение коэффициентов ряда Лорана. Неравенство Коши. Теорема Лиувиля. Пусть f(z) аналитична в кольце k: r|z-z0|R |Ck|=(1/2)C(|f()|/(|-z0|)k+1)|d| =(1/2)(M()/k+1)2=M()/k=|Ck|=M()/k. M()=max|f()|, C.C|d|=2. Теорема Лиувиля. Если f(z) аналитична и ограничена на комплексной плоскости C то она является постоянной. Доказательство. По теореме Лорана в кольце 0|z|+ (центр-начало координат r=0,R=+все комплексные плоскости) {{{ Теорема Лорана(о разложимости аналитической в кольце функции в ряд Лорана.)Если функция f(z) аналитична в кольце k: 0r|z-z0|R=+ то она в этом кольце представима рядом Лорана: f(z)= k=-+ Ck(z-z0)k (2) где Ck=1/2iCf()/(-z0)k+1d (3) C : |-z0|=, rR }}}. f(z)= k=- Ckzk , где |Ck|=M/k так как M=const ,-произвольнаяСk=0 и при k=0 остаются только C0. Отсюда следует, что f(z)=C0=const.
|
|
24. Изолированные особые точки, их классификация. Поведение аналит.фун-и в окр.изолиров.точек различ типов. Опредение Пусть D обл. аналитичности функции f(z), каждую точку аналитичн. функции f в обл. D мы назыв. правильной точкой. Граничные точки обл. аналитичности D мы назыв. особыми (.). Определение
Особая т.
Классификация особых точек: Если z0 изолир. особая т. функции f(z), то существ. 3 взаимноисключ. друг друга случаи: 1)В
лорановском разлож. все коэфф. правой
части равны нулю:
2)Главная
часть содерж. лишь конечное число
коэфф. ≠0,
т.е.
3)Главная часть содерж. ∞ много ≠0 коэфф., тогда z0 — существенно особая точка функции f(z). Теорема 1 (Устранимая особая точка) Если z0 — изолированная особая точка, то выполняются след. утверждения: 1)z0 — устранимая особая точка,
Док-во:
1)
2)
3)
|
Определение. Если
f(z)
аналитична в т. z0
и
Теорема 2 (о поведении функции в окрестности полюса). Если Z0 изолир. особая т. функции f(z), то след. условия эквивалентны: 1) z0 — полюс n-го порядка функции f(z).
Док-во: 1) 2)
Значит
выполняется (1) и
3)
Тогда
|
|
25. Теорема Сохоцкого. Теорема. Если z0C – существенно особая точка для F(z), то для любой АС существует последовательность {zk}(k: zkz0, zk->z0), такая, что limk->f(zk)=A. Док-во. 1. Пусть A= => F(z) не ограничена в каждой окресности z0 (>0 и M>0 z: 0<|z-z0|< => |F(z)|>M). В частности nN zn : 0<|zn-z0|<1/n и |f(zn)|>n => {zk}k: zkz0, zk->z0) и f(zn)-> при n->. 2. Пусть A. Может случиться ,что в окрестности z0 - F(z)=A, тогда теорема справделива. Пусть F(z)A в достаточно малой окрестности z0, тогда (z)=1/(F(z)-A) будет аналитична в этой окресности всюду, кроме, быть может z0, которая является изолированной особой точкой, эта z0 может быть только существенно особой точкой, т.к. если бы существовал конечный или бесконечный limz->z0(z) (т.е. z0 была бы устранимой или полюсом), то существовал бы конечный или бесконечный limz->z0F(z)=limz->z0[A+1/(z)], что для F(z) невозможно, т.к. z0 – существенно особая точка => z0 – существенно особая точка для (z), но тогда по доказанному в п. 1 существует {zn}-> z0, такая, что limz->z0(z)= => limz->z0f(z)=A. |
|
|
26. Вычет аналитической функции в изолированной особой точке. Вычисление вычета с помощью производной. Вычет в изолированной особой точке () . Пусть zk – изолир. особая точка функции F(z), тогда она аналитична в некотором кольце К: 0<|z-z0|<R. Опр 1. Вычетом функции F(z) в изолир. особой точке z0 называется число Resz=z0[F(z)]=(1/2i)CF(z)dz (1). C: |z-z0|=, 0<<R. Зам 1. Если - любая кусочно-замкн. кривая Жордана и К, то по обобщенной теореме Коши: Resz=z0[F(z)]=(1/2i)+F(z)dz (2). Зам 2. По теореме Лорана в кольце К: F(z)=k=-k=+[Ck(z-z0)k], Ck=(1/2i)Сρ[F(z)/(z-z0)k+1]dz; R=0;±1; ±2; При k=(-1),то Resz=z0[F(z)]=(1/2i)CF(z)dz=C-1 (3). Зам 3 (вычисление вычетов с помощью производной). Пусть z0 - полюс порядка n аналит. функции F(z), F(z)=C-n(z-z0)-n +…+ C-1(z-z0)-1 + C0 + C1(z-z0) +C2(z-z0)2+… (ряд Лорана), C-n≠0. Домножая обе части равенства на (z-z0)n,получим (z-z0)n F(z)=C-n +…+ C-1(z-z0)n-1 + C0(z-z0)n + C1(z-z0) n+1 +… дифференцируя (n-1) раз и переходя к пределу z->z0 получаем: C-1= Resz=z0[F(z)]= =[1/(n-1)!]*limz->z0(dn-1/dzn-1) [(z-z0)n F(z)] (4). |
26. Зам 4. Пусть z0-полюс 1 порядка, тогда Resz->z0[F(z)]= =lim z->z0((z-z0)F(z)) (5) Зам 5. Пусть z0-полюс 1 порядка для F(z)=φ(z)/ψ(z), где φ(z) и ψ(z)-аналит. в кольце К, причем φ(z0)≠0, ψ(z0)=0, ψ’(z)≠0.Тогда согл-но формуле (5) Resz->z0[φ(z)/ψ(z)]=limz->z0[(z-z0)*(z)/(z)]= =limz->z0[(z)/[((z)-(z0))/(z-z0)]]=(z0)/’(z0) (6). Опр 1. (Вычисление в ). Пусть z= - изолир. особая точка для аналит. ф-ции F(z), тогда существует кольцо К: R<|z|< где F(z) – аналитична. Опр 2. Вычетом функции F(z) в изолир. особой точке назыв. число Resz=[F(z)]=(1/2i)CF(z)dz (7). C: |z|=, R<<+. Зам 6. Т.к. в кольце R<|z|<+ F(z)= k=-k=+ [Ck*zk] (представимо рядом Лорана), где Ck=(1/2i)C[F(z)/zk+1]dz,где к=0;≠1,.. то С-1= (1/2i)CF(z)dz= -(1/2i)C-F(z)dz => Resz=[F(z)]= -C-1. (8)
|
|
27. Основная теорема о вычетах. Теорема о сумме вычетов. Теорема 1 (основная). Пусть D – конечная произвольная область, ограниченная кусочно-гладкой кривой C, а функция F(z) аналитична в D и непрерывна в замкн. области D*=DC всюду, кроме конечного числа изолир. особых точек akD, k=1,…,n. Тогда СF(z)dz=2i*k=1n Resz=ak[F(z)] – сумма вычетов (1). Док-во. Построим круги Dk: |z-ak|<k c границей Ck:|z-ak|=ρk, круги принадлежат D и попарно не пересекаются, т.е. DD*=DкCк, Dк∩̷Cк= пустое множ-во, к≠0. Применим обобщенную теорему Коши к (n+1) связной области D**=Dk=1nDк*. Граница этой области С**=СС1*…Сn* : СF(z)dz=k=1n[СkF(z)dz]=2i*k=1n[(1/2i)СkF(z)dz]= =2i*k=1nResz=zk[F(z)]
чтд
Теорема 2 (о сумме вычетов). Если функция F(z) аналитична на комплексной плоскости всюду, кроме конечного числа точек a1…an, то k=1∞ Resz=ak[F(z)]+ Resz=[F(z)] = 0 (1). Док-во. Пусть CR: |z|=R – окружность столь большого радиуса, что k: |ak|<R, тогда на основе теоремы вычетов СRF(z)dz= =2i*k=1∞
Resz=ak[F(z)],
но СrF(z)dz=
-(Сr-F(z)dz)=
-2i*Resz=[F(z)]
=> k=1∞
Resz=ak[F(z)]+
Resz=[F(z)]
= 0
|
|
|
28. Вычисление интегралов с бесконечными пределами с помощью вычетов. Лемма 1. Пусть функция F(z), z=x+iy аналитична в полуплоскости ImZ >0, всюду, кроме конечного числа особых точек zk, причем на действительной оси ImZ=y=0 может иметь полюсы первого порядка. Тогда если limR->[maxzCr|zF(z)|]=0,где CR–верхняя полуокр-ть (|z|=R, ImZ>0), то -+ F(x)dx=2i*k=1n Resz=zk[F(z)]+ i*p=1m Resz=zp[F(z)] (1), где zk – ос. точки функции F(z) на ImZ>0, zp – ос. точки функции F(z) на y=0. Интеграл (1) понимается в смысле главного значения. Док-во. Для простоты полагаем, что F(z) на действ. оси имеет только полюс 1 порядка в т.z=. Рассмотрим замкнутый контур С=СR [-R,z]Cr[+r,R], где CR: |z|=R- полуокр-ть настолько большого радиуса, что max|zk|<R, max|zp|<R, а Cr : |z-α|=r Imz> полуокр-ть настолько малого радиуса, что F(z) аналитична в 0<|z-|<r (кольце). По основной теореме о вычетах (Теорема 1 (основная). Пусть D – конечная произвольная область, ограниченная кусочно-гладкой кривой C, а функция F(z) аналитична в D и непрерывна в замкн. области D*=DC всюду, кроме конечного числа изолир. особых точек akD, k=1,…,n. Тогда СF(z)dz=2i*k=1n Resz=ak[F(z)] – сумма вычетов) СF(z)dz=(СR+ -R - r+ Сr+ +rR)F(z)dz =2i*k=1n Resz=zk[F(z)] (2) По условию Леммы >0 R0()>0 что при z: |z|>R0: |zF(z)|</. Тогда если R>R0,то|СRF(z)dz|<СR|zF(z)|*|dz/z|</*R/R= => limR->[ СRF(z)dz]=0 (3) На окружности теорема доказана. Рассмотрим ось X. F(z) аналитична в кольце 0<|z-|<r и отсюда следует, что по теорема Лорана (если f(z) аналитическая в кольце 0<r<|z-z0|<R<+∞, то она в этом кольце представима рядом Лорана: f(z)=к=1∑к=∞[Ск(z-z0)k, где Ck=(1/2πi)*Cρ∫[f(ξ)/(ξ-z0)k+1dξ, k=0,±1,±2…, Cρ: |ξ-z0|=ρ, z<ρ<R) она представима в виде: F(z)=C-1/(z-)+(z) (4) (z) – аналитична и ограничена на Cr. С-1= =Resz=[F(z)].Тогда СRF(z)dz=С-1*Crdz dz /(z-) + Cr(z)dz = -iС-1 + +Cr(z)dz, т.к.: 1) C+dz/(z-)=2 на |z-|=r. 2) M>0: |(z)|<M на Cr и |Cr(z)dz|< Cr|(z)||dz| < M*r*0d=*M*r, поскольку z=|z|*exp(i) => dz=i|z|exp(i)d => |dz|=|z|d=rd. |
Таким образом принимая во внимание пункты 1 и 2 и переходя к пределу, получаем limr->0[СrF(z)dz]=( -iResz=[F(z)] ) (5). Переходя в (2) при r->0, R->+ и учитывая (5), получим (-+f(x)dx)=2i*k=1nResz=zk[F(z)]+i*Resz=[F(z)].
Лемма 2. Пусть f(z)-аналит. при Imz > 0 всюду, кроме конеч. числа точек zk и zp, причем на действ. оси (Imz=0) она может иметь разве лишь полюсы первого порядка, тогда R->∞limzCRmax|f(z)|=0,где СR:{|z|=R, Imz > 0},то для λмнож-ву дейст. чисел: -∞∫+∞eiλxf(x)dx=2πik∑Resz = zkeiλxf(z)+πip∑Resz = zpeiλxf(z) (1) Zk: ImZk>0 Zp: ImZp=0 при этом интеграл (1) понимается в смысле главного значения. Док-во: не умаляя общности, предположим, что на действ. оси сущ-ет полюс 1 порядка z=α.Тогда для замкн. контура С(см.рис к лемме1), внутри которого находятся все ос. точки, имеем: C∫eiλzf(z)dz=( R∫+-R∫α-r +Cr∫+ α+r∫R ) eiλzf(z)dz=2πik∑z=zkRes eiλzf(z); (z->0, R->∞) : -∞∫+∞eiλxf(x)dx=2πik∑Resz=zkeiλxf(z)+πip∑Resz=zpeiλxf(z) Следствие. Пусть f(x)-действ. функция с действ. переменной, тогда eiλxf(x)=f(x)cosλx+if(z)sinλx, и, выделяя действ. и мнимую части, получим: -∞∫+∞ f(x)cosλxdx= -2πIm[∑z=zkRes eiλzf(z) + +0.5∑ z=zpRes eiλzf(z)] -∞∫+∞f(z)sinλxdx=2πRe[∑z=zkRes eiλzf(z) + 0.5∑ z=zpRes eiλzf(z)]
|
|
29. Оригинал и изображение по Лапласу. Лемма об абсолютной сходимости интеграла Опр 1. Всякая комлекснозначная функция F(t) действительной переменной t (-<t<+) назыв. оригиналом, если она удовлетворяет трем условиям: 1) F(t)0 при t<0. 2) F(t) непрерывна на любом конечном отрезке оси t, всюду быть может за искл. конечного числа точек, где она может иметь разрывы 1 рода. 3) При t->+ F(t) растет не быстрее экспоненты, т.е. M=M(f)>0 и S=S(f)>0, что |F(t)|<M*exp(St) (1). Пусть {S} – множество всех значений S, для которых справедливо (1), тогда S0=inf{S} назыв. показателем роста F(t) при t->+. Опр 2. Изображением или образом (по Лапласу) оригинала F(t) назыв. функция F(p), p=S+i, которая определяется по формуле F(p)=0+exp(-pt)*F(t)dt (2). Обозначение F(p)÷f(t) или f(t)÷F(p) F(p)=L[f] или f=L-1[F], L-оператор Лапласа Лемма 1. Если F(t) является оригиналом, то для n=0,1,2… интеграл 0+(dn[exp(-pt)*F(t)]/dpn)dt сходится абсолютно в области Re(p)> >S0. Док-во. |0+(dn[exp(-pt)*F(t)]/dpn)dt|=|0+((-t)n exp(-pt)*F(t))dt| < < 0+(tn |exp(-pt)|*|F(t)|)dt < M*0+(tn exp((-S-S0)t))dt (3). Пояснение : |F(t)|<=M*exp(S0t), |exp(-pt)|=|exp(-(S+i)t) |=exp(-St). Интегрируем по частям: 0+((tn) exp(-(S-S0)t))dt=[-tn/(S-S0)]exp(-(S-S0)t)t=0|t= + +[n/(S-S0)]0+((tn-1) exp(-(S-S0)t))dt=[n/(S-S0)]0+(tn-1 exp(-(S-S0)t))dt = … =[n!/(S-S0)n]0+ exp(-(S-S0)t)dt= n!/(S-S0)n+1 < n!/(-S0)n+1 (4). Итак, |0+(dn[exp(-pt)*F(t)]/dpn)dt| < 0+|dn[exp(-pt)*F(t)]/dpn|dt < < n!/(-S0)n+1=const. (5).
|
30. Теорема об аналитичности изображения оригинала. Теорема. Изображение F(p)=0+exp(-pt)*F(t)dt оригинала F(t) является аналитической функцией в области Re(p)>S0, где S0 – показатель роста, причем в этой области F(n)(p)= =0+(dn[exp(-pt)*F(t)]/dpn)dt, n=0,1,2,.. Док-во. (Проведем для n=1,для остальных аналогичное док-во) R(p, p)=(F(p+p)-F(p))/p - 0+(-t*exp(-pt)*F(t))dt= =0+(exp(-pt)*F(t)[exp(-pt)/p + t – 1/p])dt. Оценим величину в [ ]: |exp(-pt)/p+t–1/p| = |k=1[(-t*p)k/(k!* p)]+t| = = |k=2(-t*p)k/(k!*p)| = |t2p*k=2(-t*p)k-2/k!| = =|t2p*k=0(-t*p)k/((k+2)!)| < t2|p|*k=0(t*|p|)k/k!= t2|p|exp(|p|t). Таким образом: |R(p, p)| < M*|p|0+ t2exp(-(S-S0-|p|)t)dt; |R(p, p)| < 2M*|p|/(S-S0-|p|)3. При p->0 получаем, что R(p, p)->0. Мы док-ли F(n)(p)=0+(dn[exp(-pt)*F(t)]/dpn)dt при n=1. [F(p+∆p)F(p)]/ ∆p -> F’(p) при ∆p->0. |
|
31. Теорема обращения (представление оригинала по его изображению) Теорема:
Если F(p)
– изображение кусочно-гладкой
функции-оригинала f(t)
в области Rep>s0,
то в точках непрерывности f(t)=(1/2pi)
a-i¥òa+i¥eptF(p)dp
(1), где интеграл берется вдоль прямой
Rep=a>s0
Доказательство: Рассмотрим функцию j(t)= e-atf(t). Эта функция является также кусочно-гладкой и, т.к. |f(t)|£Me-s0t, то: |j(t)|=Me-(a-s0)t и => limj(t)=0 (t->¥). Это значит, что j(t) представима интегралом Фурье. e-atf(t)= j(t)=(1/2p)-¥ò+¥dx-¥ò+¥j(h)eix(t-h)dh, т.к. j(h)=0 при h<0; e-atf(t)=(1/2p)-¥ò+¥dx0ò+¥j(h)eix(t-h)dh |*eat; f(t)=(1/2p)-¥ò+¥e-atf(t)=j(t)=(1/2p)-¥ò+¥e(a+ix)tdx0ò+¥e-(a+ix)hf(h)dh; f(t)=(1/2p)-¥ò+¥e(a+ix)tF(a+ix)dx (2). F – образ f. Сделаем замену: a+ix=p. f(t)=(1/2pi) a-i¥òa+i¥eptF(p)dp, ч.т.д. Оригинал f(t) однозначно отображается через изображение F(p) с точностью до значений в точках разрыва функций f(t).
|
32. Линейность преобразования Лапласа и теорема подобия. Теорема: Если для i=1, 2,.., n: fi(t) ¸Fi(p) "i: Rep>si, тогда для "с1,.., сn: i=1åncifi(t)¸i=1ånciFi(p), Rep>maxsi (1<i<n) Доказательство: (основано на линейности оператора Лапласа) 0ò+¥e-pti=1åncifi(t)dt=i=1ånci0ò+¥e-ptfi(t)dt= i=1ånciFi(p), ч.т.д. Теорема подобия: Eсли f(t)¸F(p), то для "a>0: f(at)¸(1/a)F(p/a), Rep>as0 Доказательство: Сделаем замену: at=x 0ò+¥e-ptf(at)dt=(1/a)0ò+¥e-(p/a)xf(x)dx=(1/a)F(p/a), ч.т.д. |
|
33. Теоремы о дифференцировании оригинала и изображения. Теорема: Если f(t)¸F(p), Rep>s0, то f ’(t)¸pF(p)-f(0) (1) Если f(n)(t) – оригинал, то f(n)(t)¸pnF(p)-pn-1f(0)-pn-2f ’(0)-…-f(n-1)(0), Rep>s0 (2) Доказательство: (для формулы(1)) f’(t)¸ 0ò+¥e-ptf’(t)dt=e-ptf(t)t=0½t=+¥+p*0ò+¥e-ptf(t)dt=pF(p)-f(0), ч.т.д. Теорема д-ии из-ия: Если F(p)¸f(t), Rep>s0, то F’(p)¸(-t)f(t) (1) И вообще, n-ая производная: F(n)(p)¸(-t)nf(t), Rep>s0 (2) Доказательство: Согласно Тh1 {{. Теорема об аналитичности изображения оригинала. . Изображение F(p)=0+exp(-pt)*F(t)dt оригинала F(t) является аналитичной функцией в области Re(p)>S0, где S0 – показатель роста, причем в этой области F(n)(p)=0+(dn[exp(-pt)*F(t)]/dpn)dt. }}, F(n)(p)= (dn/dpn) 0ò+¥e-ptf(t)dt= 0ò+¥e-pt[(-t)nf(t)]dt¸(-t)nf(t), ч.т.д.
|
34. Теорема об интегрировании оригинала. Теорема: Если f(t) ¸F(p), Rep>s0, то 0òtf(x)dx¸F(p)/p, Rep>s0 Доказательство: Легко проверить, что если f(t) – оригинал, то и функция g(t)= 0òtf(x)dx - оригинал. Пусть g(t)¸G(p). Тогда по Св3 (диф. оригинала){{ Теорема: Если F(p)¸f(t), Rep>s0, то F’(p)¸-tf(t) (1) И вообще, n-ая производная: F(n)(p)¸(-t)nf(t), Rep>s0 (2) }}, g’(t)¸pG(p)-g(0), g(0)=0, g'(t)=f’(t), f(t)¸pG(p), f(t)¸F(p) => G(p)=F(p)/p, т.е. F(p)/p=G(p)¸g(t)= 0òtf(x)dx, ч.т.д. Следствие: Если f(t)¸F(p), то 0òtdt10òtdt2…0òtf(tn)dtn¸(1/pn)F(p) |
|
35. Теорема об интегрировании изображения. Теорема: Если f(t) ¸F(p), Rep>s0 и f(t)/t – оригинал, то f(t)/t ¸ 0ò+¥f(q)dq Доказательство: Пусть функция Q(q)= 0ò+¥e-qt(f(t)/t)dt – изображение f(t)/t. Согласно следствию из Л1, Q(¥)=0. Дифференцируя обе части этого равенства, причем для правой части возможно дифференцирование под знаком интеграла, согласно Teoreme{{. Теорема об аналитичности изображения оригинала.. Изображение F(p)=0+exp(-pt)*F(t)dt оригинала F(t) является аналитичной функцией в области Re(p)>S0, где S0 – показатель роста, причем в этой области F(n)(p)=0+(dn[exp(-pt)*F(t)]/dpn)dt. }} возможно, получим: Q’(q)=- 0ò+¥(-t)e-qt(f(t)/t)dt=-F(q). Интегрируем это равенство от p до ¥: Q(+¥)-Q(p)= - pò+¥F(q)dq, Q(¥)=0, Q(p)= pò+¥F(q)dq, ч.т.д.
|
36. Теоремы запаздывания и смещения. Th. Запаздывания. Если f(t) F(p) Re(p)>S0 при 0<<+ то для ф-ии f = {f(t-), t ; 0, t<.} То имеет место соотношение f(t) e-pF(p) (1) Док-во: Т.к. f(t-) = 0 при t<, то: f(t) 0e-ptf(t)dt = e-ptf(t-)dt = 0e-p(+)f()d = e-p0e-pf()d = e-pF(p). Th. Смещения. Если f(t) F(p) Re(p)>S0 то для p0 C : ep0tf(t) F(p-p0), Re(p) > S0 + Re(p0). Док-во: ep0tf(t) - оригинал с показателем роста S0 + Re(p0); тогда ep0tf(t) 0e-ptep0tf(t)dt = 0e-(p-p0)tf(t)dt = F(p-p0). |
|
37. Th. Умножения (свертки). Если f(t) F(p); Re(p) > S1 ; g(t) G(p); Re(p) > S2 , то произведение образов F(p) и G(p) также является образом, причем: F(p)G(p) 0tf()g(t-)d; Re(p) > max{S1,S2}. Док-во: Докажем сначала, что (t) = 0tf()g(t-)d - является оригиналом. Первые два условия существования оригинала очевидны. Пусть |f(t)| M1eS1t; |g(t)| M2eS2t;пусть M = max{M1,M2}; S0 = max{S1,S2}. Тогда: |0tf()g(t-)d| 0t|f()||g(t-)|d < M1M2* 0te-S0eS0(t-)dt M2eS0t < M*e(S0+)t ; >0; d=0|t=t; t<eεt т.к. infε>0(S0+ε)= S0 то показатель роста нашей ф-ии = S0 а M*=M2 3е условие существования оригинала выполняется (t) = 0tf()g(t-)d 0e-pt0tf()g(t-)d. Изменим порядок интегрирования: (t) = 0f()d e-ptg(t-)dt = {замена t- = ; t = +} = 0e-pf()d0e-pg()d = F(p)G(p). Замечание: 0tf()g(t-)d - наз. сверткой f и g и обозначается (fg)(t) = 0tf()g(t-)d т.е. произведению изображений соответствует свертка оригиналов. (fg) = (gf). Свертка симметрична 0tg()f(t-)d=(gf)(t) |
38. Первая теорема разложения Хевисайда Th. Пусть функция F(p)-аналитична в некоторой кольцевой окрестности точки ∞,R<|p|<+∞ и имеет в этой окрестности Лорановское разложение: F(p) = k=1∑∞[C-k/pk] (1) Тогда оригиналом F(p) будет функция: f(t)={ k=1∑∞[C-k/(k-1)!]*tk-1, t>0 ; 0, t<0 (2) Док-во: k=1∑∞С-k/pk=[1/p]*k=1∑∞C-k/pk-1, точка р=∞ является устранимой для ряда: k=1∑∞C-k/pk-1,следовательно при |p|≥ρ>R ƎA>0 так что |k=1∑∞C-k/pk-1|<A=const Тогда при |p|≥ρ>R: |k=1∑∞C-k/pk|=|F(p)|<A/ρ=M(ρ) Согласно неравенству Коши для коэф. ряда Лорана имеем |C-k|<M(ρ)/(ρ-k )= M(ρ)ρk = Aρk-1, k=1,2,3… отсюда имеем, |k=1∑∞[C-k/(k-1)!]*tk-1| k=1∑∞|C-k|*[|t|k-1/(k-1)!] < A*k=1∑∞[(ρ|t|)k-1/(k-1)!] = Aeρ|t| Ряд (2) мажорируется стремящимся степенным рядом и сл-но сход. равномерно при |t| r,r≠∞ и ряд (3) k=1∑∞[C-k/(k-1)!]*tk-1 –сход. равномерно в круге |t|<r. Умножим (3) на e-pt и результат почленно проинтегрируем на (0;r). 0r e-pt k=1∑∞[C-k/(k-1)!]*tk-1dt = k=1∑∞[C-k/(k-1)!]0r e-pttk-1dt (4); tnn!/pn+1 и 0∞ e-pttk-1dt(k-1)!/pk. Переходя в (4) к пределу при r→∞: 0∞ e-pt k=1∑∞[C-k/(k-1)!]*tk-1dt = k=1∑∞[C-k/pk] = F(p)# |
|
39.Вторая теорема разложения Хевисайда (без док-ва) Th. Пусть ф-ция F(p) удовлетворяет следующим условиям 1.F(p)-аналитична на всей комплексной плоскости кроме конечного числа особых точек, которые являются полюсами этой функции 2. В области Re(p)>S0; F(p)-аналитическая 3.F(p)→0 равномерно при р→∞ относительно arg(p) 4.Для любого a>S0 сходится интеграл: a-i∞∫a+i∞|F(p)|*|dp|. Тогда оригиналом функции F(p) является функция f(t) = k∑Res ep*tF(p) {p = pk - написать под Res} t>0; 0, t<0.
|
40.Интеграл Дюамеля и его применение По Th диф. оригинала f ’(t) ÷ pF(p) - f(0) (1). Запишем теорему умножения: F(p)*G(p) ÷ 0∫tf()g(t-)d (2); f(t) ÷ F(p); g(t)÷G(p), тогда pF(p)G(p) = f(0)G(p)+(pF(p)-f(0)) G(p) ÷ f(0) g(t) + 0∫tf ’()g(t-)d (3). В этой формуле мы исп: pF(p)-f(0) ÷ f ’(t); т.к. свертка симметрична pF(p)G(p) ÷ f(0)g(t) + 0∫tg()f ’(t-)d (4). Поменяем ролями F(p) и G(p): pF(p)G(p) ÷ g(0) f(t) + 0∫tg’()f(t-)d = g(0)f(t) + 0∫tf()g’(t-)d (5). Применение интеграла Дюамеля Пусть требуется решить ЛДУ с пост. коэф. при нулевых начальных усл.: L[x] = f(t) (6). Пусть известно решение x1(t) урав. L[x]=1 (7), также при нулевых нач. усл. Воспользуемся интегралом Дюамеля для реш (6) Опер. урав-ния соответственно (6) и (7): A(p)X(p) = F(p) (8); A(p)X1(p)=1/p (9); x1(t) ÷ X1(t); x(t) ÷ X(p); f(t)÷F(p); X(p) = pX1(p)F(p) (10); по ф-ле Дюамеля x(t)=0∫tf()x'1(t-)d (11); x(t)=x1(t)f(0) + 0∫tx1(t)f’(t-)d (12); f(0)=0 |
|
41.Импульсная функция и её изображение по Лапласу. Некоторые св-ва δ функцию δh={0,t<0,t>h;1/h,0<t<h. Действует на отр [0;h], причем -∞∫+∞ δh(t)dt=0∫hdt/h=1;(2) При h->0 получаем последовательность {δh(t)}, которая яв-ся расходящейся. Введём условную функцию δ(t), которую будем считать пределом этого семейства ф-ий δ(t)=limh->0δh(t) (3) Эта функция называется импульсной функцией нулевого порядка или δ-функцией,или ф-ией Дирака.Эта ф-ия всюду=0 кроме точки t=0,где она δ(0)=∞ и -∞∫+∞ δ(t)dt=1. Изображение δ-функции. δh(t)=1/h[η(t)- η(t-h)] (5). По теореме запаздывания δ(t)÷ [1/h][(1/p)-(1/p)(e^(-ph))] δ(t)÷ limh->0[1-e^(-ph)]/ph=1.(6) Рассмотрим график интеграла ф-ии η(t)=0∫t δh(τ) dτ (7) ηh(t)->η(t) при t->0; δ(t)= η’(t) (9). Преобразуем соотношение (6) η(t) ÷1/p; δ(t)÷ p/p=1. Значение оригинала при t=0 считаем=0.Для любой ф-ии оригинала φ(t) получаем 0∫∞φ(t) δh(t)dt=[1/h]0∫h φ(t)dt переходя к пределу h->0 0∫∞φ(t) δ(t)dt=φ(0) (10). Если φ(t) разрывна при t=0 то под φ(0) будем понимать правое предельное значение δ(t)÷ 0∫∞[e^(-pt)] δ(t)dt=e^(-pt)│t=0=1 На δ-функц. распространяются основные операционного исчисления. 1)Теорема запаздывания δ(t-τ)=e^(-p τ); 0∫∞[e^(-pt)]δ(t- τ)dt= e^(-pt) │t=τ=e^(-pτ) 2)Теорема умножения F(p) ÷ 0∫tf(τ)δ(t-τ)dτ=f(τ) t=τ =f(t);
|
42. Передаточная ф-ия и ее применение к решению задач электротехники. Рассмотрим неоднородное ЛДУ n-ого порядка y(n)+Cn-1y(n-1)+…+C1y1+C0y=f(t) (1). Пусть заданы начальные условия y(0),y`(0), …,y(n-1)(0) (2). Представим решение задачи Коши в виде суммы y=y1+y2 (3). y1: y1(n)+Cn-1y1(n-1)+…+C1y1(1)+C0y1=f(t), y1(0)=…=y1(n-1)(0)=0} (4) y2: y2(n)+Cn-1y2(n-1)+…+C1y2(1)+C0y2=0, y2(0),…,y2(n-1)(0)} (5). Сумма решений (4) и (5) даст общее решение задачи (1),(2). Рассмотрим задачу (4). y(t)÷Y(p) операторные уравнения: pnY1+Cn-1pn-1Y1+…+C1p1Y1=F(p) (6), где Y1(p)÷y1(t), F(p)÷f(t). Введем обозначения: pn+Cn-1pn-1+…+C1p1=q(p), q(p)Y1(p)=F(p), Y1(p)=1/q(p)*F(p) (7). Обозначим 1/q(p) через G(p), тогда Y1(p)=G(p)F(p) (8). Применив теор о свертке сразу получаем искомое решение y1 задачи (4). y1(t)=g(t)f(t)=0∫tg(τ)f(t-τ)dτ (9). Применение задачи (4) к решению задач по электротехнике. В зад.(4) назовем f(t)-входная функция, а y(t) – выходная функция. При нулевых нач дан на эл цепь описыв (4) действует только возбуждающая ф-я f(t), а y(t) – отклик на возбуждение. В пространстве изображений F(p) – входная ф-я(возб), а Y(p) – вых ф-я (отклик на возбуждение). Связь имеет вид Y(p)=G(p)F(p) (10). (для удобства заменяем Y1(p)=Y(p)). Функция G(p) зависит от постоянных Cn-1,…,C1,C0, т.е. от внутр стркуктуры эл цепи, она связывает ф-и Y(p) и F(p). Она назыв коэфф передачи или передаточной ф-ей. Соотв ф-я в пр-ве оригиналов называется ф-ей Грина для задачи (4). Схематическая связь между F;Y;G: F → G → Y. Пусть теперь несколько физ систем соединены между собой. Например входная ф-я первой системы и выходная второй: F→ G → Y → G1 → Y1. Y=GF, Y1=G1Y, след-но Y1=GG1F след-но F → GG1 → Y1. Рисунок. Выходная ф-я Y1 блока G питает G1, находящ на линии обратной связи с вых ф-ей Y2, она подвод к D, к которой так же подается входная функция F, в результате создается F-Y2 или F+Y2 – как угодно, кот снова подается на блок. Y1=G(F-Y2), Y2=G1Y1, Y1=(G/GG1+1)F, H=G/GG1+1. |
|
43. Дискретное преобразование Лапласа, связь с импульсной ф-ией. Дискретное преобразование Лапласа. В прилож вместо f(t) может быть задана последовательность значений {fn}, n=0,1,2…через опред промежуток времени t=0,1,2…Преобр-е Лапласа примен для ф-ции можно применить и к последовательности, если их заменить ступенчатой ф-ей f0(t)=fn, n≤t≤n+1, n=0,1,2…(1). Ф-я f0(t) явл кусочно-пост и ее образ, согласно преобо Лапласа, имеет след вид: F0(p)=n=0∑∞n∫n+1e-ptfndt= n=0∑∞fn(e-np-e-(n+1)p)/p= (1-e-p)/p(n=0∑∞fne-np) (2). Запись (2) можно упростить, если отбросить множитель 1-e-p/p, тогда в правой части (2) ост только n=0∑∞fne-np – как результат непосредственных преобр посл-ти {fn}. Это преобразование обозн символом Д, и называется дискретным преобр Лапласа Д[fn]≡ n=0∑∞fne-np. Замечание: Д-преобр можно рассматривать как преобр Лапласа но не ф-ции, а распределения. Последоват fn=f(n) выдел из f(t) может быть рассм как результат импульсов δ(t-n) извлеч из f(t) в t=n знач ф-ции f(n). Совокупность этих импульсов моделируется посредством ф-ии f(t). В рез-те получаем f(t)= n=0∑∞f(t-n)= n=0∑∞f(n)δ(t-n)= f*(t). Ф-ю f*(t) будем называть распределением. Применив к f*(t) преобразование Лапласа, получим:L[n=0∑∞f(n)δ(t-n)]= n=0∑∞f(n)L[δ(t-n)]= n=0∑∞fne-np=Д[f(n)] (4). Д[f(n)] – дискретное преобразование Лапласа(применено к распред{fn}). (4) следует из теор запаздывания для δ(t): δ(t-τ) ÷e-pτ ;(τ=h). Д[f(n)]=L[f*(t)] (5). Таким образом дискретное преобраз-е есть преобраз-е Лапласа некоторого распределения. |
44. Z – преобразование, примеры. Z – преобразование. Введем новую переменную z=ep. Тогда ряд n=0∑∞fne-np переходит в ряд по степеням 1/z и преобразование принимает след вид: F*(z)= n=0∑∞fnz-n=Z[fn] (1). F*(z)=Z[fn]. fn÷F*(z). Замечание1: преобразования L,Z,Д связаны м/у собой след соотношением: L[f*]=Д[fn]=Z[fn]|z=ep=F*(ep) (2). Замечание2: Ряд (1) сходится вне некоторого круга комплексной пл-ти |z|>R≥0. Поэтому все особенности изображения F* находятся внутри круга |z|≤R. Пример1. Найти z – преобр fn=eαn. F*(z)= n=0∑∞eαnz-n= n=0∑∞(eαz-1)n=1/(1-eαz-1)=z/(z-eα). |z|>eRe α. Положим α=0. fn≡1, F*(z)= z/z-1÷fn=1. Пример2. Если cos, то cosα=(eiα+e-iα)/2. Пример3. fn=1/n. n≥0, f0=0. F*(z)= n=0∑∞z-n/n= n=0∑∞1/nzn=ln(1/z-1).
|
|
45. Обращение Z – преобразования. Обращение
z-преобразований.
1). Согласно ф-ле для коэф ряда Лорана
fn=1/(2πi)|z|=r∫F*(z)dz/z1-n
(1), n=0,1,2…r<R.
Внутри окр |z|=r
должны быть все особенности ф-ци F*(z).
2). z=reiφ.
fn=
|
46. Целые ф-ии и их св-ва. Целые ф-ии: Однозначная ф-ия f(z) наз. целой если она аналитична во всей комплексной пл-ти С. {Напр.: ez; Cosz; Sinz;…} Опр. Ф-ия наз целой-рациональной, если полюсом для нее явл. т-ка z = , если же т-ка z = - существенно особая т-ка, то ф-ия наз. трансцендентной. Th 1. Если т-ка z = - явл. устранимой особой т-кой целой ф-ии f(z), то f(z) = const. Док-во: По условию Th. Lim(f(z)) = A при z, тогда для >0 R() >0 z: |z|>R |f(z)-A|< ||f(z)|-|A|| |f(z)-A| < |f(z)| < |A| + = M1, |z| >R. Т.к f(z) аналитична в круге |z|R, то M2, что |f(z)| < M2< |z|R. Пусть теперь M = max{M1,M2}, тогда для z С: |f(z)|M. Отсюда по Th (Лиувиля) f(z) = const. Th
2. Если
Док-во:
т.к.
|
|
47.Мероморфные ф-ии, рациональные ф-ии.Представимость рациональной ф-ии в виде суммы многочлена и простейших дробей. Опр. Однозначная ф-ия f(z) наз мероморфной на компл пл-ти С, если в огр части пл-ти С она не имеет никаких других особых точек, кроме полюсов. Примеры: Pn(z)/Qm(z) – дробно-рац. ф-ии; tg(z); ctg(z);… Замечание: В огр части компл пл-ти мероморфная ф-ия имеет конечное число полюсов, в противном случае в этой части пл-ти предельная т-ка мн-ва полюсов, и тогда эта т-ка не явл изолированной т-кой для полюсов. Th 3. Если т-ка z= - полюс мероморфной ф-ии f(z), то f(z) - рациональная ф-ия. Док-во:
Т.к. z=
- изолированная особая т-ка, то
кольцо R<|z|<
в котором f(z)
- аналитическая, в круге |z|R
по условию имеет лишь конечное число
полюсов, поэтому в пл-ти f(z)
Следствие: Всякую рациональную ф-ию можно представить в виде конечной суммы многочлена и простейших дробей вида: [C/(z-zк)] и это представление единственно. Док-во:
Особыми т-ками рациональной ф-ии на |
48. Св-во единственности для регулярной ф-ии. Th 1. Если f(z) /0 регулярная (аналитическая) в нек области, то она в этой области может иметь только изолированные нули. # Th 2 (Th единственности). Если 2 регулярные в области D ф-ии f1(z) и f2(z) совпадают на некоторой бесконечной последовательности попарно различных т-к z1…zn, сходящейся к z0 D, то в области D: f1(z) = f2(z). Док-во: Рассмотрим регул ф-ию (z) = f1(z) - f2(z), все т-ки z1…zn - есть нули этой ф-ии т.к. (zk) = 0, k = 1…n… т.к. limzk=z0 при k, то в следствии непрер. (z0) = limf(zk)=0 при k. Здесь z0 – также нуль ф-ии (z), но т-ка z0 не явл изол нулем ф-ии (z), поскольку в ее окр имеются другие нули zk по Th 1. (z)0 в окр т-ки z0, тогда все ее коэф Тейлора = 0 в нек круге с центром в z0 и радиусом = расстоянию от z0 до ближайшей т-ки границы области D f1(z) f2(z) поскольку (z) 0. Докажем, что f1(a) = f2(a) в т-ке обл D. Соединим z0 и а кусочно гладкой кривой , целиком леж в D. Пусть 2>0 - кратчайшее расстояние точек до границы области D. Опишем вокруг z0 окружность с радиусом , соглано доказ. заключаем, что во внутр т-ках g0 этой окружности: f1(z) f2(z). Пусть z01 - первая при движении от z0 к а по т-ка пересечения этой окр-ти с кривой , проведем окр с рад , с центром в z01, пусть g1 - внутр этой окр-ти в окр т-ки z01 имеет беск попарно разл точек g0 в которых f1(z) f2(z) согласно уже док в круге g1 всюду f1(z) f2(z), продолжая этот процесс мы в конце концов получаем, что f1(a) f2(a). Следствие: Если 2 аналитические ф-ии совпадают на сколь угодно малой области или на сколь угодно малой дуге кривой, то они всюду совпадают в области своего определения.
|
|
49.Понятие аналитического продолжения ф-ции. Опред1. 1)Пусть ф-я f(z) определена на мн-ве E;2) Ф-я F(z) аналитична в обл Д, причем Е – часть области Д.3)F(z)≡f(z) в E,тогда ф-ия F(z) наз-ся аналитическим продолжением f(z) множ-ва Е в области Д Тh1.(принцип аналитического продолжения)Пусть множ-во Е имеет предельную точку Z0 принадлежащую Д, тогда аналитическое продолжение с мн-ва Е на мн-во Д единственно. Д-во:Предположим,что f(t) определённое на Е имеет 2 аналитических продолжения F1(z), F2(z) в области Д, F1(z) ≡F2(z) для z ЄЕ то по теор. единственности F1(z) ≡F2(z) в Д. Если Е-кривая в Д то сущ-ет не более 1 аналитического продолжения f(z) на Д. Th2.Пусть f(z) и g(z) целые ф-ии то есть регулярные или аналитические во всей комплексной плоскости. Тогда f(z)±g(z); f(z)*g(z) f(g(z)) будут также целые ф-ии. Д-во:Следует из определения целой ф-ии и св-в регулярной ф-ии.
|
49. Пример:Аналитическое продолжение f(z)=n=0∑∞zn (ряд сходится в круге К: |z|<1) ф-ия регулярна(аналит)в данном круге=>f(z)=1/[1-z] в К,а F(z) аналитична в Д(Д-регулярная расширенная комплексная плоскость,С с выколотой точкой 1).при |z|<1 f(z)≡F(z)=>F(z)-!аналитическое продолжение ф-ии f(z) с мн-ва К наД. Аналитическое продолжение экспоненты,тригонометрических и гиперболических ф-ий e^z= n=0∑∞zn/n! (по опред.)ряд в правой части сходится при всех z => сумма ряда аналитична при всех z. При действит z=x ф-ия e^z совпадает с естественной ф-ией e^z=e^x (на действительной оси)=>ф-ия e^z-аналитическое прод-ие e^x с действительной оси на комплекную плоскость.Введём ф-ию:sin(z),cos(z),sh(z),ch(z) как суммы степенных рядов: sin(z)= n=0∑∞[(-1)^n]*[(z^(2n+1))/(2n+1)!]; cos(z)= n=0∑∞[(-1)^n]*[(z^(2n))/(2n)!]; sh(z)= n=0∑∞(z^(2n+1))/(2n+1)!]; ch(z)= n=0∑∞(z^(2n))/(2n)!]; т.к .все ряды сход-ся при всех z, то эти ф-ии целые,они –аналитические продолжения ф-ии sin(x);cos(x);sh(x);ch(x) с действит оси на комплекс. пл-ти. |

 0 при
Dz
0 при
Dz
 =0
=0 (1) – аналитич. в D
(1) – аналитич. в D =0
=0 (1) – аналитич. в D
(1) – аналитич. в D =0, то f(z)
– аналитична в D.
=0, то f(z)
– аналитична в D. наз-ся изолированной, если существ.
U(
наз-ся изолированной, если существ.
U(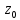 )
такая, что f(z)
аналитическая и однозначная всюду
кроме т. z0,
где функция f(z)
возможно неопредел.
)
такая, что f(z)
аналитическая и однозначная всюду
кроме т. z0,
где функция f(z)
возможно неопредел.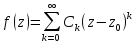 ,
такая т. назыв. устранимой;
,
такая т. назыв. устранимой;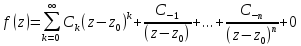 ,
тогда точка z0
— полюс
n-го
порядка.
,
тогда точка z0
— полюс
n-го
порядка.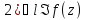 при
при
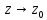
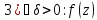 аналитична в
кольце
аналитична в
кольце
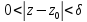 .
.
 ;
;
 ,
такая что
,
такая что
 в кольце
в кольце
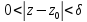 ,
тогда
,
тогда
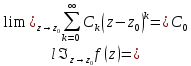 .
.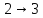 ;
Дано
;
Дано
 ,
т.к.
,
т.к.
 аналитична и непр. в некот. кольце
аналитична и непр. в некот. кольце
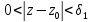 ,
то вследствии непр. в замкнут. обл.,
,
то вследствии непр. в замкнут. обл.,
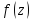 огранич. в этой обл.
огранич. в этой обл.
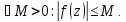
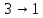 ;
По теореме Лорана
;
По теореме Лорана
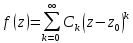 ,
согласно нер-ву Коши
,
согласно нер-ву Коши
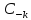 ,
k=1,2,…;
,
k=1,2,…;
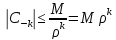 ,
где
,
где
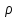 — произв. число:
— произв. число:
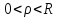 .
Значит
.
Значит
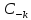 =0,
при k=1,2,…
=0,
при k=1,2,…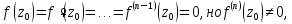 то z0
наз-ся нулём кратности n
функции f(z).
При этом C0=C1=…Cn-1=0,
Cn≠0.
то z0
наз-ся нулём кратности n
функции f(z).
При этом C0=C1=…Cn-1=0,
Cn≠0.
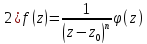 ,
где
,
где
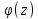 — аналитична в т. z0
и
— аналитична в т. z0
и
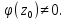
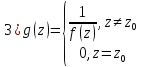 (1) аналитичка в
т.
(1) аналитичка в
т.
 и
и
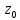 есть ноль функции
есть ноль функции
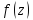 n-го
порядка.
n-го
порядка. .
.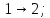 Пусть z0
полюс n-го
порядка, тогда
Пусть z0
полюс n-го
порядка, тогда
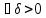 ,
что в кольце K:
,
что в кольце K:
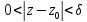 и
и
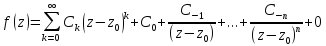 .
Можем переписать в виде:
.
Можем переписать в виде:
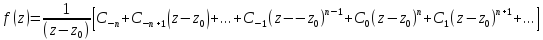 или
или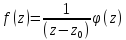 ;
;
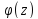 аналитична в круге
аналитична в круге
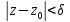 как сумма степенного ряда и
как сумма степенного ряда и
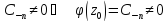 .
.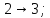
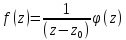 ,
,
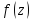 аналитична в U(z0)
и
аналитична в U(z0)
и
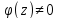
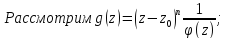
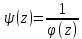 есть аналитич.
функция как частное двух аналит.
функций, причем
есть аналитич.
функция как частное двух аналит.
функций, причем
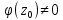 .
Поэтому функция
.
Поэтому функция
 может быть разложена в ряд Тейлора:
может быть разложена в ряд Тейлора:
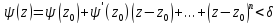 ,
но
,
но
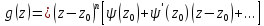 .
Отметим, что
.
Отметим, что
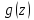 есть ряд Тейлора как произвед. двух
аналит. функций.
есть ряд Тейлора как произвед. двух
аналит. функций.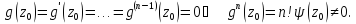
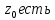 ноль
g(z)
n-ого
порядка и g(
ноль
g(z)
n-ого
порядка и g(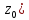 =0.
=0.
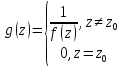 ,
,
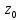 — есть ноль n-го
порядка для функции g.
Тогда
— есть ноль n-го
порядка для функции g.
Тогда
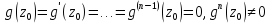 или
или

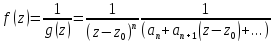 ,
,
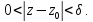
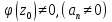 и функция
и функция
 аналитична в т.
аналитична в т.
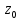 как частное двух аналитич. функций.
След-но, функцию
как частное двух аналитич. функций.
След-но, функцию
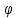 можно разлож. в ряд Тейлора в
можно разлож. в ряд Тейлора в
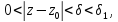
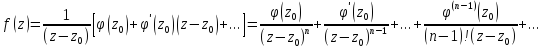 ;
где
;
где
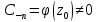 .
Это означ., что
.
Это означ., что
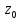 ,
есть полюс n-го
порядка для функции
,
есть полюс n-го
порядка для функции
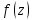 .
.


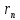 /2π-π
∫πF*(
reiφ)
einφdφ(2).
, где fn/
/2π-π
∫πF*(
reiφ)
einφdφ(2).
, где fn/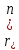 – коэфф Фурье для F*(
reiφ).
3). Т.к. ряд F*(z-1)
– есть ряд по возрастающим степеням
– коэфф Фурье для F*(
reiφ).
3). Т.к. ряд F*(z-1)
– есть ряд по возрастающим степеням
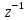 ,
то по ф-ле Тейлора fn=1/n!(dnF*(z-1)/dzn)|z=0,
n=0,1,2…(3).
4). Th(о
предельном значении). Если изображение
F*(z)=Z[fn]
– сущ, то f0=z→∞limF*(z).
без док-ва. Следствие: Очевидно, что
ряды: z(F*(z)-fn)
=f1+f2z-1+f3z-2+…
z2(F*(z)-f0-f1z-1)=f2+f3z-1+…
итд представляют собой z-преобразования,
поэтому, определив по Th
значение f0:
f1=z→∞limz(F*(z)-f0)
(4), f2=z→∞limz2(F*(z)-f0-f1x-1)
(5) итд
,
то по ф-ле Тейлора fn=1/n!(dnF*(z-1)/dzn)|z=0,
n=0,1,2…(3).
4). Th(о
предельном значении). Если изображение
F*(z)=Z[fn]
– сущ, то f0=z→∞limF*(z).
без док-ва. Следствие: Очевидно, что
ряды: z(F*(z)-fn)
=f1+f2z-1+f3z-2+…
z2(F*(z)-f0-f1z-1)=f2+f3z-1+…
итд представляют собой z-преобразования,
поэтому, определив по Th
значение f0:
f1=z→∞limz(F*(z)-f0)
(4), f2=z→∞limz2(F*(z)-f0-f1x-1)
(5) итд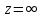 –
полюс кратности n
(n
–
полюс кратности n
(n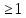 )
целой функции f(z),
то эта функция есть многочлен n-ой
степени
)
целой функции f(z),
то эта функция есть многочлен n-ой
степени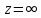 - полюс кратности n,
то ряд Лорана принимает вид:
- полюс кратности n,
то ряд Лорана принимает вид:
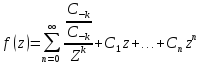 ,
,
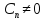 .
Введем обознач.:
.
Введем обознач.:
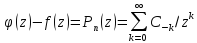 ,
где
,
где
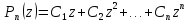 .
Очевидно, что
.
Очевидно, что
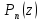 - целая функция, поэтому
- целая функция, поэтому
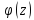 как разность целых функций также целая
функция. Т.к. Разложение лорана функции
как разность целых функций также целая
функция. Т.к. Разложение лорана функции
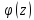 не содержит главной части, то точка
не содержит главной части, то точка
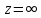 является устранимой для
является устранимой для
 .
Тогда по теореме 1
.
Тогда по теореме 1
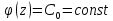 и
и
