21. Принцип максимума модуля.

Лемма: Знач-ие голоморф. в обл. G ф-ии f в любой т. z равно среднему арифм. ее значений на любой окр-ти Г с центром z, принадл. вместе с внутренностью обл. G.

Теорема 1: Если ф. f голоморф. в обл. G с С_z и модуль |f| достигает локал. максимума в нек. т. z_0,то ф. f=const в G.

Док-во: Положим |f(z₀)|=M, очевидно, 0≤M<. Выберем числотак, чтобы кругU(z₀,) вместе с границей лежал вG и чтобы |f(z)|≤M в замыкании z. В случ. M=0 имеем f=0,и, согласно принципу единств-и, f=0 в G. Пусть M>0. Рассужд. от прот-го, покаж., что |f|=M в . Предпол., что вимеется некот. т., где 0<r<, 0≤t₀≤ 2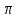, в кот. |f(z^*)|<M, тогда в виду непрер-ти )|т., что наT₁=[t₀-,t₀+] выполн. нер-во. Кроме того, ф , 0≤≤M на дополн. T₂= [t₀+,t₀-+2]. Используя теор. о среднем для голоморф. ф-ции, имеемf(z₀)=. ОткудаПолученное противоречие доказ., что |f|=M в U(z₀,

Следствие1: Максимум |f|, голоморф. в обл. и непрер. в ее замыкании, может достигаться только на границе этой обл., при усл-иии, что f(z)≠const.

Следствие 2(Вейерштрасса): Пусть дан ряд f₁(z)+…+f_n(z)+… (1) все члены кот.- ф-ции, голоморф. в обл. G и непрер. в G, тогда если ряд (1) сход. равном. на границе обл. G , то он сход-ся также равномер. на замкн. обл..

22.Нули голоморф.ф-и. Порядок нуля. Изолированность нулей голоморф.ф-и.

Опр. Если ф-яголоморфн. в обл-ти, то кажд. т. , в кот., наз. нулем ф-ии.

Утв. замкнут.огранич. подмн-во обл-тиG, в кот. ф-я fголоморф. и , может содерж. лишь конечное число нулей ф-иf.

Док-во. Д-но, предположение по -ти мн-ва нулей приводит к-ию вGхотя бы 1-й предел. т. мн-ва ф-и fи, сл-но, к рав-вуf=0.

Утв.Мн-во нулей голоморф.вG ф-ии(fкак эл-т, вектор), конечно или счетно.

Док-во.Обл-тьGможно представ. в виде объединения замкн. мн-в ,, где– расст. отzдо . Т.к. в кажд.мн-во нулей ф.fконечно, то в Gоно конечно или счетно.

Опр.Пусть fголоморф.вобл-тиG, ,–т. обл-тиG, . Числоmназ. порядком (кратностью) нуля ф-ииf, если ее разложение в ряд Тейл. в окр. т. имеет вид:(,. Очев, что т.явл. нулем пор-каm голоморф.ф. fтиттк,.

Пример. Т. явл. для ф-ииsinz-z нулем пор-ка 3, а т. для ф-ииsinzнулем пор-ка 1.Опр. При m=1 нуль ф. f наз. простым.

Утв. Голоморф.ф., имеющая нули, либо тожд. нулю, либо ее нули – изолир. т. (без док-ва).

23. Представление рядом Лорана ф-и, голоморф.в кольце. Интегральные ф-лы Коши для коэфф-в ряда Лорана.

Теор. 1. Пусть ф-я fголоморф.в кольце, ,, тогда вKф. fпредставима в виде суммы f=S+T, где S(z) – сумма степ. ряда , сходящ. в круге, а–сумма ф-ии ряда, сходящ. вне замыкания круга. Коэф. этих рядов выраж. ф-лой:(1), где.

Док-во.Зафикс. т. и возьмем числатак, что выполн.. Пустьсоотв-но внутр. и внешн. граничн. окр-ти кольца. Пусть– окр-ть с центр. в т.z, леж. внутри . Т.к.явл. голоморф. ф. отв обл-ти К, исключая т., то по интегр. т. Коши для остального контура имеем, откуда, где,. Разложим подынтегр. ф. в 1-м из интегралов по полож, а во 2-м – по отриц. степеням разности:;. Получ. ряды сход.равном. соотв-но на,, т.к.при,ипри,, поэтому после почленного интегрир. рядов получ. разлож.,с коэф-ами:,. Ряд с суммойS(z) сход.в круге , а ряд с сум.T(z) сход-ся вне замык. круга . Т.к. ф-яприголоморф.при, то в силу интегр. т. Коши о составном конт., интегрирование поив ф-лахиможно заменитьинтегрир-ем поокр-тис центр. в т., лежащей в кольце К. 1-й ряд в теор. 1S(z) –обыкн. степ. ряд и изображ. ф-ю f, голоморф. в круге . 2-й рядT(z) можно рассм. как обыкн. степ.ряд, если ,. В новых обозначениях ряд примет вид(3). Ряд (3) сход.прии изображ. ф. перем.t и голоморф. при . Возвращаясь к перем.z, видим, что ряд T(z) изобр. T(z), голом. вне замкн. круга . Преставл. голоморф.ф.с коэф.

1. можно запис. короче .

24.Ряд Лорана, его правильная и главная части. Единственность ряда Лорана.

[ P.S. Теор. 1. Пусть ф-я fголоморф.в кольце , ,, тогда вKф. fпредставима в виде суммы f=S+T, где S(z) – сумма степ. ряда , сходящ. в круге, а–сумма ф-ии ряда, сходящ. вне замыкания круга. Коэф. этих рядов выраж. ф-лой:(1), где. ]

Опр.Разлож. (откуда получилось – см. билет 22) по целым степеням наз. рядом Лорана ф.fв кольце К. СуммаS(z) с неотриц. степенями наз. егоправильной частью, а сумма T(z) с отриц. степенями – главной частью.

Теор. В данном круговом кольце голоморф.ф.f(z) единств. образом разлагается в ряд Лорана.

Док-во. Пусть (5) на окр-ти, где. Ряд (5) сход.равном. Умножив (5) на, получ.. Здсеь ряд также сход.равномерно на, поэтому, интегрир. его почленно на, получ:, что совпад. с (1).

25.Прав.иизолиров. особые т. голоморф. ф-и. Критерий прав.т. Классификация особых изолир. т-к. Ряд Лорана в окрестности особ.т.

Пусть ф-я f(z) явл. голоморф.внекот. окр-ти.

Опр. 1.Если такое, что, положив, получ. ф-юf(z), голоморф.во всем круге , то т.наз.правильной т. ф. f(z). Если такого числа не , то т.наз.изолир. особ.т. для ф. f(z).

Теор. Для того, чтобы ф. f(z), голоморф.вбыла правильн. в т., необх. и достат., чтобыокр-тьUт. , в кот.f(z) огранич. по модулю.

Док-во.Необх. очевидна. Достат. – много.

Следствие. Чтобы т. была изолир. особ. т.f(z) необх. и достат., чтобы вееокр-ти|f(z)| был неогранич., т.е. чтобы выполн. .

Опр. 2.Изолир. особ.т. , для кот. выполн., наз.полюсом голоморф. ф. f.Изолир. особ.т., для кот. (ни конечн., ни бескон)наз. существ. особ. т. ф.

Теор. 2. Чтобы т. была полюсом ф.f(z) необх. и достат., чтобы эта т. была нулем ф. .

Док-во. Большое.

Опр. 3. Т. наз. полюсом порядка (кратности)m, если т. явл. нулем порядкаm для ф. . Приm=1 полюс наз. простым, а при m>1 – кратным.

Теор. 3. Чтобы т. была полюсом кратн.m для ф. f, необх. и достат., чтобы лорановск. разлож. ф. f(см. 22-23) имело вид: ) (3).

Док-во. Большое.

След.Изолир. особ.т. голоморф. ф.f(z) явл. для нее существенно особ. т. титткларановск. разлож. ф. fв окр. т. содержитмн-во членов с отриц. степенями.

26.Теорема Сохоцкого.

Теор. 1.Если –сущ. особ. т. голоморф. ф. f, то для сущ. сход. кпослед-ть, такая, чтопри.

Док-во. Большое. [Случай бескон. удал. т.Пусть f(z) голоморф. в , тогда ф.будет голоморф.в обл.,.

Опр. 1. наз. прав. т., полюсом порядка mили сущ. особ. т. ф. f(z), голоморф. в К, (см. 25) в зав-ти от того, будет ли т. соотв-но прав. т., полюсом порядкаm или сущ. особ. т. для ф-ии. В указ. случ. ф.иммет в окр-ти т.имеет лоран. разлож. (см. 23) вида:, второе ур-ие не видно.(в посл. случ. беск. мн-во коэф.при отриц. степеняхотлична от 0).

Опр. 2.Разлож. , голоморф. в кольце, ф.f в ряд Лорана наз. рядом Лорана в бесконечности. Главная часть (см. 24) ряда Лорана в беск-ти наз. совокупность членов с полож. степенями, а прав.частью – все ост. члены.]