13 Интегральная формула Коши. Теорема о среднем

. Теор: Пусть G-односвязанная область, ограниченная Жардановой спрямляемой кривой Г. f(z)-голоморфная функция замкнутой области G, тогда для точки справедлива формула:(1) (кривая Г проходится в положительном направлении)

Док-во: фиксир. . Пусть- окружность радиусаρ с центром в точке z, целиком лежащей в G. РИС. Рассмотрим так же функцию (2). Эта функция является голоморфной в области, лежащей между контурами Г и, включая контура.

На основании теоремы Коши (3), это рав-во показывает, что.

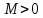Из рав-ва 2 =>, что , когда. Положив, получим непрерывно замкнутую областьфункции. Сл-но, что. Откуда получаем:, откуда следует, что, т.ксколь угодно мало, а значпостоянное число.

Рав-во 3 примет вид ,или

Опред: мн-л наз интегралом Коши.

Во всякой т. z не принадлеж ин-л Коши по теор Коши =0.

Поскольку ф в этом случае является голоморфной в

РИС

14. Теорема Тейлора о разложении голоморфной функции в степенной ряд. Следствия: существование у голоморфной функции производных всех порядков, интегральная формула для производных.

ТеоремаПусть f(z) – голоморфная, z∈G, R.В круге K_R={z:|z-z₀|<R}, функция f(z) представляется в виде степенного ряда:

Доказательство:z∈K_ρ, рассмотри коцентрический круг радиуса(0<<R), содержащий z.

При фиксированном z последний ряд равномерно сходится на Г_ρ (ξ∈Г_ρ).

так что можно воспользоваться мажорантным признаком Вейерштрассе равномерной сходимости ряда. В (2) законно почленное интегрирование ряда (3):

Следствие 1Каждая функция f(z), голоморфная в области G имеет производную всех порядков в этой области.Следствие 2 Следствие 3

15. Неравенства Коши для коэффициентов степенного ряда и теорема Лиувилля. Основная теорема алгебры.Теорема 1 (неравенства Коши)

Неравенства (3) называются неравенствами Коши.

Доказательство:

Теорема 2 (теорема Лиувилля)

Если функция f(z) голоморфна на всей плоскости C_z, и |f(z)|<M, M>0, то f(z)=const

Доказательство:

Радиус сходимости разложения (1) равен бесконечности, т.е. неравенства (3) имеют место для ⱯR>0. Отсюда получим: a_n=0, при (n=1,2,…). И стало быть f(z)=a₀=const

Теорема 3 (основная теорема алгебры)

Всякий многочлен p(z)=c₀+c₁z+…+c_nzⁿ (n≥0, c_n≠0) имеет хотя бы один нуль.

Доказательство:

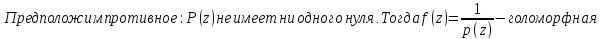
По т. Лиувилля f(z)=const=0, что противоречит определению этой функции.

ч.т.д.

16. Теорема о существовании первообразной у голоморфной функции. Формула Ньютона-Лейбница.

Теорема 1

Если функция f(z) голоморфна в односвязной области G, то значения интеграла

и конечного пути интегрирования.

Теорема 2

Пусть f(z) – функция, неприрывная в односвязной области G, для которой итегралы вдоль любых спрямляемых кривых, принадлежащих области, зависят только от начальных и конечных точек

F’(z)=f(z)

Определение

Назовем функцию Ф(z) голоморфную в области G первообразной для функции f(z), если Ф'(z)=f(z).

Теорема 3

Любая первообразная Ф(z) от голоморфной в области G функции f(z) выражается формулой:

Доказательство:

ч.т.д.

Полагая в (1) z=z₀, получим: Ф(z₀)=с, поэтому из (1) следует формула Ньютона-Лейбница: