5. Метод макс правдоподобия. Опр неизвестных параметров нормального закона распределения.
Для точечной оценки неизв параметров распредел.
А. Непрерывные СВ
Х – непрерывная СВ; н-число испытаний; х1...хn– знач Х в рез-те испытаний ;
f(х)
– вид плотности распределения;
- параметр, определяющийf(х)
– неизвестен.
Ф-ция
правдоподобия Х– ф-ция аргумента
:L(х1,х2,….,хn;
)=f(x1;
)…..f(xn;
),
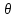где х1…хн – фиксированные числа.
В
качестве точечной оценки параметра
принимается такое его значение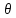
*
=
*(х1…хn),
при котором ф-уия правдоподобия L
достигнетmax.
Оценка
*- оценка наибольшего правдоподобия.
Методпоиска точки ф-цииlnLаргумента
:
1)
найти 1ую производную dlnL/d
2) приравнять производную к 0, найти критические точки (корень полученного уравнения)
3)
найти 2ую производную d2lnL/d
2
Если
2ая производная при
=
*
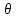отрицательна, то =>
*
- т.max
и
=>
*
- оценка наоб правдоподобия параметра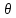
Определение неизв параметров НЗР
В рез-те испытаний Х принимает знач х1…хn. Определить Мх- ? и σх- ?
Решение.
1=Mx
2
=σx
1)
L(x1…xn;
)=L(x1…xn;
)=p(x1;λ)…p(xi;λ)
=> L= (λx1*e-λ)/x1! … (λxi*e-λ)/xi!= (λ*∑xi*e-nλ)/x1!...xn!
2) lnL= (∑xi)*lnλ-nλ-ln(x1!...xn!)
3)
dlnL/dλ=∑(xi)/(λ) -n=0 из
этого выражаемλλ
=
=x̅в
4) d2 ln L / d λ 2 = -n/ λ 2 <0 => Mx – t. max
=> Мх* = Хв- несмещенная оценка
σх* =Dв– смещенная оценка
6. Метод макс правдоподобия. Определение неизвестных параметров нормального закона Пуассона.
Для точечной оценки неизв параметров распредел.
В. Дискретные СВ
Х – дискретная СВ; х1…хн – знач, которые принимает Х в рез-те н опытов; н – кол-во опытов;
- неизв параметр
опр з-н (вид з-на задан); р(хi;
)
– вероятность того, что в рез-те испытаний
величина Х примет знач хi(i=1,2,…n)
L(х1,х2,….,хн;
)=р(x1;
)…..р(xn;
), где х1…хn–
фиксированные числа.
*- точечная оценка параметра
.
*=
*
(х1…хn) при
знач которогоLдостигаетmax
Метод
нахождения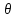
*
1)
найти 1ую производную dlnL/d
2) приравнять производную к 0, найти критические точки (корень полученного уравнения)
3)
найти 2ую производную d2lnL/d
2
Если
2ая производная при
=
*
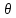отрицательна, то =>
*
- т.max
и
=>
*
- оценка наоб правдоподобия параметра
Определение неизвестных параметров норм з-на Пуассона
Pm(Х=хi)=
, где м- число сделанных испытаний,
х – число появления события вi-ом
опыте (i=1,2…n);
(1 опыт состоит из м испытаний). Требуется
определить λ-?
Решение.
1=λ
1)
L(х1,х2,….,хn;
)=L(х1,х2,….,хn;
λ)= р(x1;
)…..р(xn;
)=
=> L =
2) ln L = (∑x)*ln L – n*λ – ln(x1!x2!...xn!)
3) dln L / d λ = ∑x / λ – n = 0 из этого выражаем λ λ= ∑x/n = Хв
4) d2lnL / dλ2 = -∑x / λ2 (при λ=Хв ) <0 => λ=Хв – t. max => λ*=Хв –оценка параметра λ з-на Пуассона.
7. Метод моментов. Примеры оценки по методу моментов.
Для точечной оценки параметров распределения.
Суть: приравнивание опр кол-ва выборочных моментов р-мого распределения к соотв кол-ву теоритических моментов того же порядка. В качестве моментов р-мся нач и центральные моменты.
Начальные моменты
Теоретические υk=M(Xk) υ1=M(X1) υ2=M(X2)
Эмпирические
Mk=
∑ni*xi^k=x̅в =>M1=x̅в
Центральные моменты
Теоретические Mk=M[(X-M(X))k] => 0=M1 ;Dx=M2=M[(X-M(X))2]
Эмпирические
mk=
∑ni(xi-x̅в)k
=>m2=
∑n2(x2-x̅в)2=Dв
f(x;θ) – вид плотности распределения – задан. θ – неизвестный параметр, определяющийf(x;θ)
нужно найти точечную оценку θ θ*=ψ(х1…хn)
Приравниваем:
υ1=М1} (нач моменты)
υ1=М(Х) } => М(Х) = Хв
=>
М(Х)l= ∫ хl
*f(x;θ)dx= φ (θ) =
* ∑xl,гдеl=1,2…. – номер
момента.
Примеры оценки по методу моментов
Пр1.
Показательный з-н распредел. По выборке х1…хnтребуется найти оценку параметра λ-?
Показательный з-н: f(x;λ)=λ*e-λ*x x>=0
Т.к. неизвестен всего лишь 1 параметр = > для его определения необходимо 1 ур-ие, т.е. l=1
x>=0
=> ∫0∞ xλe-λ*xdx= 1/λ;
=
*
∑x= Хв=> λ = 1/Хв;
λ* = 1/Хв = n/ ∑x
Пр2.
Норм з-н распределения. Найти по выборкуе х1…хnнеизв параметрыMx-? σ-?
По опр Мх– момент 1го порядка
Мх= ∫x1f(x,mx,σx^2)dx=
∑xi=x̅в
По опр Dх– момент второго порядка
Dх
= ∫x1f(x-mx)2f(x,mx,σx^2)=
∑(xi-x̅в)2=Dв
Мх* = Хв
σх* = √Dв