
- •Пояснительная записка к дипломному проекту на тему: «вязкое затухание звуковых волн в сильных центробежных полях»
- •Оглавление
- •Глава 1 Литературный обзор 7
- •Глава 2 Методика расчета 25
- •Аннотация
- •Введение
- •Глава 1 Литературный обзор
- •Поведение газа в центробежном поле сил
- •Волны в сильном центробежном поле
- •Затухание звуковых волн
- •Глава 2 Методика расчета
- •Постановка задачи
- •Теоретический анализ
- •Описание программы
- •Верификация
- •Заключение
- •Список литературы
Теоретический анализ
Получим аналитическое выражение для декремента затухания волн, поляризованных вдоль оси вращения в центробежном поле сил. Для этого запишем систему уравнений для аксиальной компоненты скорости в цилиндрической системе координатах:


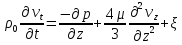

Подставляя выражение
 ,
и решая систему получим следующее
уравнение:
,
и решая систему получим следующее
уравнение:
 .
(2.10)
.
(2.10)
Решение уравнения (2.10) будет состоять из общего однородного и частного неоднородного:
 .
.
Решая общее однородное уравнение
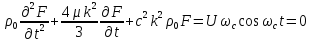 ,
,
получим:
 .
.
Решая частное неоднородное уравнение

получим:
 .
.
Их сумма запишется как:

Усредняя, получаем:
 .
.
Так как энергия пропорциональна квадрату скорости, окончательно получим:
 ,
,
где
 -
нормировочная постоянная.
-
нормировочная постоянная.
Так как вторая вязкость не внесёт значительного вклада, а теплопроводность на этом этапе не учитывается, запишем формулу (1.24) без второй вязкости и теплопроводности:
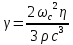
Запишем коэффициент поглощения звуковых волн в единицу времени:

Принимая во внимание то, что k=ω/cи перейдя к единым обозначениям получим выражение для распределения энергии:

где
 ,
, ,
а
,
а – нормировочная постоянная,
– нормировочная постоянная,
которое принимает вид резонансной кривой.
Теперь перейдем к выводу коэффициента затухания звука в центробежном поле сил. Для этого запишем общий вид коэффициента затухания звука в трубе без вращения [10]:

где
 .
.
Для вращающейся системы:
 ,
,
где
 .
.
Следовательно, коэффициент затухания звуковых волн в центробежном поле сил будет равен:
 ,
,
После преобразований, получаем следующую формулу для коэффициента затухания звуковых волн в центробежном поле сил выраженную через коэффициент затухания звуковых волн в покоящейся трубе:
 .
(2.11)
.
(2.11)
Описание программы
Структура программы довольно проста. Первым делом производится расчет давления и плотности газа в роторе с помощью распределений (2.6) и (2.7), после чего решается система однородных дифференциальных уравнений (2.1)-(2.5), которая после линеаризации [14] принимает вид:
 ,
,
 ,
,
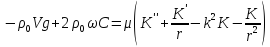 ,
,
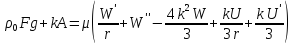 ,
,
 ,
,
 ,
,
 .
.
с граничными условиями (2.8) или (2.9).Далее по формуле:,где
считается суммарная энергия волны,По полученным значениям строится график зависимости энергии волны от ее частоты. Рис. 7
Рис.7. Пример расчетного графика зависимости энергии волны от её частоты
Далее, предполагая вид кривой, полученный в прошлой главе:
 ,
,
где aиb– искомые параметры,
проводится аппроксимация полученных
значений к данному виду, и наконец зная
численное значение
 ,
находится значение коэффициента
затухания из формулы
,
находится значение коэффициента
затухания из формулы .
.
Все вышеизложенные вычисления проводятся с заранее заданными шагом по частоте и параметрами, приведенными в таблице2.1.
Таблица 2.1. Расчетные параметры центрифуги
|
Параметр |
Значение |
|
M |
352
грамм |
|
rвнеш |
0,065 м |
|
rвнут |
0,0001 м |
|
Ω |
2π
|
|
T0 |
300 K |
|
P |
10665 Па |
|
K |
2π
|
|
cp |
385
Дж
|
|
μ |
1,83
|
|
J |
2π
|
|
Λ |
0,0061
Вт |
|
R |
8,314462
м2 |
|
G |
1,067 |
где M– молярная масса гексофторида урана (UF6),rвнеш –внешняя граница расчетов, rвнут – внутренняя граница расчетов, Ω – круговая частота вращения ротора, T0 – температура на внешней границе, p – давление на внешней границе, k – волновое число задаваемых возмущений, cp – удельная теплоемкость гексофторида уранаUF6при постоянном давлении,μ –динамическая вязкость гексофторида уранаUF6, j – частота задаваемых возмущений, λ – теплопроводность гексофторида уранаUF6,R – универсальная газовая постоянная, g – показатель адиабаты.


 моль-1
моль-1 1700 с-1
1700 с-1 10 - 2π
10 - 2π
 200
м-1
200
м-1 кг-1
кг-1
 К-1
К-1 10-5
Па
10-5
Па
 с
с 868 – 2π
868 – 2π 17376с-1
17376с-1 м-1
м-1
 К-1
К-1 кг
кг
 с-2
с-2  К-1
К-1  Моль-1
Моль-1