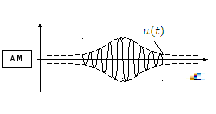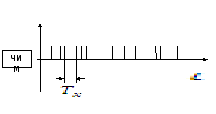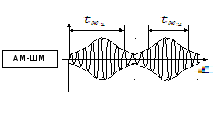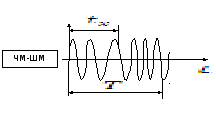Пространство сигналов
Пусть ![]() - множество сигналов.
- множество сигналов.
Путем введения
структурных ограничений из ![]() можно выделить различные функциональные
пространства. Например, ограничение
для
можно выделить различные функциональные
пространства. Например, ограничение
для ![]()
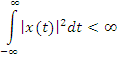
формирует Гильбертово
пространство сигналов, обозначенное
![]() .
.
Если рассматриваются периодические сигналы, то можно выделить пространство сигналов, для которых
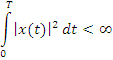
Линейное пространство
Пространство
сигналов ![]() является линейным, если для него
справедливы следующие операции:
является линейным, если для него
справедливы следующие операции:
Для ![]() определена сумма
определена сумма
![]() ,
,![]() ,
,
обладающая свойством:
-
коммутативности:
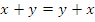
-
ассоциативности:
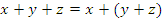
Для ![]() и числа
и числа ![]() определен сигнал
определен сигнал ![]() и при этом
и при этом ![]()
Множество ![]() содержит нулевой элемент
содержит нулевой элемент ![]() :
для
:
для ![]()
N-мерное векторное пространство
Пусть ![]() задан на
задан на ![]() .
Произведем дискретизацию (равномерную)
во времени.
.
Произведем дискретизацию (равномерную)
во времени.
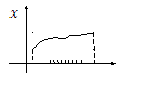
Тогда
![]() - n-мерный
вектор,
- n-мерный
вектор, ![]() – координаты вектора (сигнала). При
– координаты вектора (сигнала). При ![]() и вектор становится бесконечномерным.
и вектор становится бесконечномерным.
Представление сигналов как векторов n-мерного векторного пространства позволяет для анализа сигналов и систем использовать математический аппарат векторного анализа.
Если множество
значений координат вектора – действительные
числа, то такое векторное пространство
– Евклидово n-мерное
векторное пространство ![]() .
.
![]() -
возможное состояние или реализация
сигнала.
-
возможное состояние или реализация
сигнала.
В ![]() определены
следующие операции:
определены
следующие операции:
![]()
![]()
![]()
![]()
![]()
![]() – обратный вектор.
– обратный вектор.
Свойства операций
в ![]() :
:
![]()
![]()
![]()
![]()
в ![]() векторов
векторов ![]() ,
одна из координат которых = 1, а остальные
= 0 – координатные орты в
,
одна из координат которых = 1, а остальные
= 0 – координатные орты в ![]() .
.
![]() вектор в
вектор в ![]() может быть представлен в виде суммы:
может быть представлен в виде суммы:
![]()
![]()
………………………
![]()
Норма сигналов
Норма векторных
сигналов на ![]() – длина вектора:
– длина вектора:

Для дискретных
сигналов, определенных на ![]()

Для непрерывных сигналов:

Норма комплексных сигналов:

Метрика сигналов
Задача математической
оценки близости векторов. Предположим,
что мы задали пространство сигналов
![]() или, в частности, Евклидово n-мерное
пространство
или, в частности, Евклидово n-мерное
пространство ![]() .
.
Пусть ![]() – элементы пространства
– элементы пространства![]() (или
(или ![]() – реализации сигнала. Введем обозначения:
– реализации сигнала. Введем обозначения:
![]() – расстояние между элементами множества
– расстояние между элементами множества
![]() .
.
Введем отображение
![]() – множество действительных чисел.
– множество действительных чисел.
Если ввести правила
отображения ![]() такие, что:
такие, что:
![]()
![]()
![]()
![]()
Пространство
сигналов ![]() с введенным отображением
с введенным отображением ![]() называется метрическим.
Метрика задается нормой
разности сигналов
называется метрическим.
Метрика задается нормой
разности сигналов
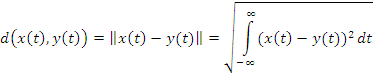
Для ![]() (Евклидово n-мерное
пространство):
(Евклидово n-мерное
пространство):

Геометрическая интерпретация для n=2:
![]()
![]()
![]()
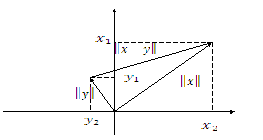
Норма сигнала = расстояние от сигнала до нулевого элемента.
Скалярное произведение векторных сигналов.
Метрика в пространстве
![]() может быть введена с помощью операции
скалярного произведения векторов.
Скалярное произведение векторов
может быть введена с помощью операции
скалярного произведения векторов.
Скалярное произведение векторов ![]() называют отображение:
называют отображение: ![]() -
поле действительных чисел, которое
обладает свойствами:
-
поле действительных чисел, которое
обладает свойствами:
![]()
![]()
Если ![]() ,
то
,
то ![]()
Если ![]() ,
то
,
то ![]()
Для скалярного произведения над полем комплексных чисел:
![]()
Введение метрики
в ![]() :
:
![]() – норма,
– норма,
![]() – расстояние.
– расстояние.
Введенные таким образом функции (отображения) полностью соответствуют требуемым свойствам метрики.
Определение
нормы и d
в ![]() в базисе.
в базисе.
Пусть в ![]() задан базис
задан базис ![]() .
Любые векторы
.
Любые векторы ![]() могут быть выражены через линейные
комбинации базисных векторов
могут быть выражены через линейные
комбинации базисных векторов ![]() :
:

Определим нормы
![]() и расстояние
и расстояние ![]() :
:
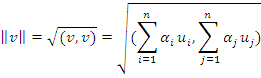
Используя 2-е и 3-е свойство
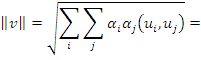
Для ортогонального
базиса ![]()
![]()
для нормированного
базиса: ![]()
![]()
Аналогично для метрики:
![]()
Пространство непрерывных сигналов (функций)
Обобщение
пространства N-мерных
векторов на аналоговые сигналы как
бесконечномерные векторы ![]() пространство
пространство ![]() (или
(или ![]() )
на
)
на ![]() .
.
Условия принадлежности
к ![]() - условия Дирихле:
- условия Дирихле:
конечное число точек разрыва 1-го рода,
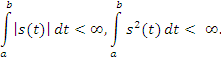
Норма сигналов в
![]() :
:
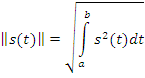
Норма, приведенная
к ![]() :
:
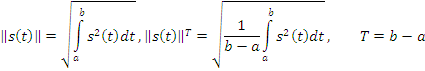
Скалярное
произведение сигналов ![]() :
:

Нормированное скалярное произведение:
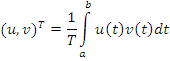
Ортогональные сигналы
![]()
![]()
![]()
Для ортогональных
сигналов:
![]()
Мощность и энергия сигнала
По определению, мощность сигнала есть
![]()
![]()
![]()
Энергия сигнала:
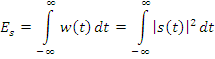
Средняя мощность
на интервале ![]() :
:
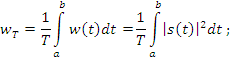
Связь энергии и нормы сигнала:
![]()
Энергия суммы сигналов:
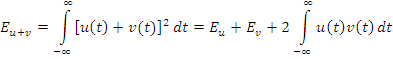
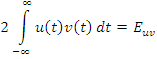
![]() – энергия взаимодействия сигналов.
– энергия взаимодействия сигналов.![]()
![]()
Ортонормированный
базис в ![]()
Ортогональный
базис: ![]()
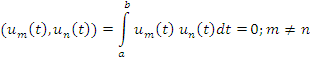
Ортонормированный базис:
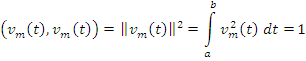
Приведение ортогонального базиса в ортонормированный:
![]()
Расположение сигналов в ряд
![]() или
или ![]() может быть разложен в ряд по системам:
может быть разложен в ряд по системам:
-
базисных функций, в том числе
-
ортогональных базисных функций, в том числе
-
ортонормированных базисных функций
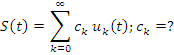
Умножим обе части
на ![]() и проинтегрируем.
и проинтегрируем.
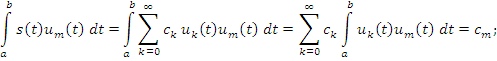
Т.е., имеем:
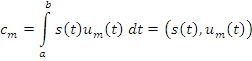
Определим разложение в ряд скалярного произведения сигналов:

![]()
![]()
Разложение энергии сигнала в ряд:
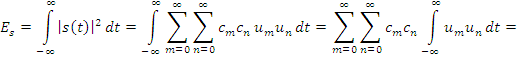
В случае ортонормированного базиса имеем:
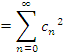
Критерии выбора системы базисных функций:
-
Для
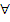 сигнала ряды разложения должны сходиться.
сигнала ряды разложения должны сходиться. -
Min числа членов разложения при заданной точности
-
Простота аналитической формы
-
Простота вычисления коэффициентов разложения
Ортонормированные системы функций:
-
Гармонические
-
Ортогональные полиномы (Эрмита, ???Лежантра, Чебышева)
-
Специальные функции (Бесселя, Лагерра, Уолсия, …)
Гармонические базисные функции
На интервале ![]() система
система ![]() .
.
Нетрудно убедиться, что имеет место быть свойство ортогональности:
![]()
![]()
Определим нормы функций:
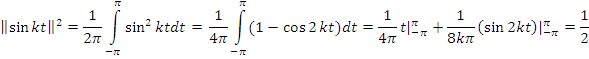
![]()
Приведем в ортонормированную систему:
![]()
Аналогично: ![]()
И объединенная sin/cos система имеет вид:
![]()
Для разложения периодического сигнала с периодом T можно использовать систему базисных тригонометрических функций:
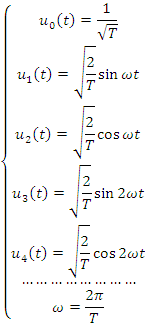
Система
ортонормированна на T.
Множитель ![]() обычно относят к коэффициентам ряда
разложения, при этом:
обычно относят к коэффициентам ряда
разложения, при этом:

Где:
![]()
Наибольшее
распространение в качестве базисных
функций частотного разложения нашли
экспоненциальные функции ![]() при
при ![]() – пр. Ф, при
– пр. Ф, при ![]() – пр. Лапласса.
– пр. Лапласса.
Связь с гармоническим разложением через формулы Эйлера:
![]()
![]()
Тогда ряд в комплексной форме:
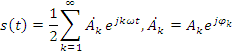
Или:
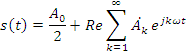
Ортонормированная система функций Уолсия
На интервале![]() система
система ![]() ,
причем
,
причем
![]()
где ![]() – функции Раденахера:
– функции Раденахера:
![]()
![]()
![]()
Система функций Уолсия – предельная модификация системы периодических функций. Удобно реализовать с помощью логических элементов (ключей) и ∑.

![]()
Спектральное представление сигнала
Обобщенный ряд Фурье.
Эйлер, Бернули – волновые процессы – любой периодический сигнал есть сумма гармонических функций. Фурье нашел решение задачи по нахождению коэффициентов рядов разложения.
Дано: ![]() – произвольные функции;
– произвольные функции;
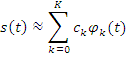
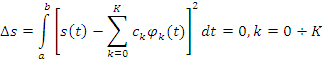
Для ортогональных
функций ![]() система имеет единственное решение,
система имеет единственное решение,![]() - линейно независимые функции.
- линейно независимые функции.
Для ортонормированного базиса (функций):
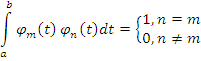
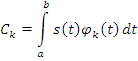
И для заданного значения K погрешность является min.
Если при ![]() ,
то система
,
то система ![]() - базисная система координат в
- базисная система координат в ![]() и при этом достигается равенство:
и при этом достигается равенство:
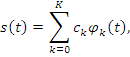
Следовательно, получен обобщенный ряд Фурье.
Разложение сигналов по гармоническим функциям.
Моды, гармоники, тригонометрические функции, экспоненциальные функции.
![]() – гармонический тригонометрический
базис. Ему эквивалентен базис
экспоненциальных функций вида:
– гармонический тригонометрический
базис. Ему эквивалентен базис
экспоненциальных функций вида:![]() .
Поскольку (тождества Эйлера)
.
Поскольку (тождества Эйлера)
![]()
И, следовательно, имеем:
![]()
Понятие собственных функций
-
Тригонометрические гармонические функции являются собственными функциями линейных операторов: сдвига, интеграла, дифференциала
-
Аналогично – экспоненциальные функции.
Проверим на операторе сдвига для тригонометрических гармонических функций. Пусть:
![]()
![]()
![]()
![]()
![]()
Проверим для экспоненциальных функций операцию переноса:
![]()
![]() -
собств. функция операции переноса, не
зависит от
-
собств. функция операции переноса, не
зависит от ![]() (собств. знач. для фиксированного значения
(собств. знач. для фиксированного значения
![]() ).
).
Для операции дифференцирования:
![]()
![]()
Для операции интегрирования:
![]()
![]()
В общем виде, для линейного оператора:
![]()
![]() - не зависит от
- не зависит от ![]() ,
собств. значение
,
собств. значение ![]()
![]() - линейный оператор.
- линейный оператор.
Спектры периодических сигналов
Спектральный анализ применяется:
-
Выявление периодических природных процессов
-
Синтез и анализ систем связи (радиосигналы и т.д.)
-
Обработка измерительных и экспериментальных данных.
-
Спектр гармоники
![]()
![]()
Действительная
часть спектра содержит общую компоненту
при ![]() с амплитудой, равной
с амплитудой, равной ![]() .
.

-
Спектры периодических сигналов произвольной формы.
![]()
Может быть разложен в гармонический ряд Фурье:

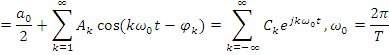
Справка:
![]()
![]()
![]()
![]()
Где:
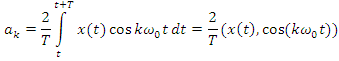
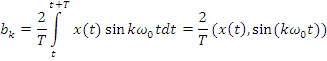
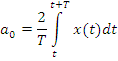
![]() – амплитудный спектр (АЧХ)
– амплитудный спектр (АЧХ)
![]() – фазовый спектр (ФЧХ)
– фазовый спектр (ФЧХ)
![]() – энергетический спектр
– энергетический спектр
![]() – комплексный спектр
– комплексный спектр
![]()
-
Спектры периодических сигналов представляют собой дискретные функции, т.к. он определен только для целых значений
 с шагом по частоте, равным
с шагом по частоте, равным
![]()
-
Первую составляющую спектра при
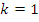 ,
равную
,
равную 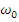 называют основной
частотой сигнала (первой гармоникой).
называют основной
частотой сигнала (первой гармоникой). -
Значения
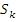 по положительным и отрицательным
значениям
по положительным и отрицательным
значениям 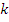 являются комплексно сопряженными.
являются комплексно сопряженными. -
Шаг по частоте
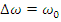 называется частотным разрешением
спектра.
называется частотным разрешением
спектра. -
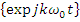 – бесконечномерный базис линейного
пространства
– бесконечномерный базис линейного
пространства 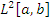 ,
а коэффициент
,
а коэффициент 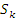 - проекции сигнала
- проекции сигнала 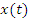 на эти базисные функции.
на эти базисные функции. -
Сигнал
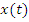 в форме ряда Ф – бесконечномерный
вектор в пространстве
в форме ряда Ф – бесконечномерный
вектор в пространстве  или точка с координатами
или точка с координатами 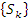 по базисным функциям
по базисным функциям 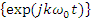 .
.
Спектры непериодических сигналов
Спектры непериодических
сигналов конечной длительности (финитных)
могут быть получены из уравнений для
рядов Ф как предельные значения при
![]() .
.
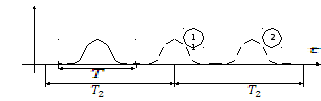
Зададим периодическую
последовательность импульсов и разложим
импульс на ![]() .
Не меняя положения импульса на
.
Не меняя положения импульса на ![]() ,
увеличим значение
,
увеличим значение![]() в два раза. При этом выражение для спектра
останется без изменения, но число
гармоник увеличится в два раза. Т.к.
в два раза. При этом выражение для спектра
останется без изменения, но число
гармоник увеличится в два раза. Т.к.
![]() ,
т.е изменяем шаг дискретизации спектра
по
,
т.е изменяем шаг дискретизации спектра
по ![]() плюс за счет множителя
плюс за счет множителя ![]() в два раза уменьшаются амплитуды
гармоник.
в два раза уменьшаются амплитуды
гармоник.
1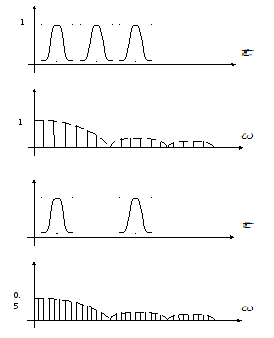
В пределе, при ![]() ,
периодическая последовательность
импульсов заменяется одиночным финитным
сигналом, дискретные частоты переходят
в непрерывную последовательность
,
периодическая последовательность
импульсов заменяется одиночным финитным
сигналом, дискретные частоты переходят
в непрерывную последовательность ![]() ,
а
,
а![]() .
Чтобы этого избежать, множитель
.
Чтобы этого избежать, множитель ![]() исключают, и мы приходим к интегралу Ф:
исключают, и мы приходим к интегралу Ф:
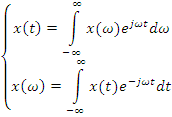
Спектр имеет смысл плотности спектра сигнала (спектральная функция сигнала)
Тригонометрическая форма интегр. Ф:
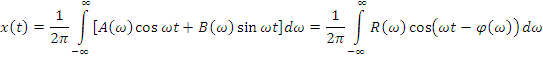
Интегр. Ф существует для сигналов, удовлетворяющих условию Дирихле или
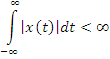
Если это условие
не выполняется, то используют другие
интегральные преобразования, в частности
преобразование Лапласа. Пусть ![]() при
при ![]() ,
а интеграл спектральной функции
расходится. Тогда
,
а интеграл спектральной функции
расходится. Тогда ![]() .
Выберем
.
Выберем ![]() так, чтобы интеграл
так, чтобы интеграл ![]() сходился, пользуемся
сходился, пользуемся

Требуем, чтобы ![]() при
при ![]() .
.
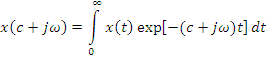
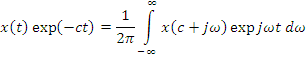
Умножая обе части
на ![]() и заменяя переменную интегрирования
и заменяя переменную интегрирования
![]() ,
получим тогда:
,
получим тогда:
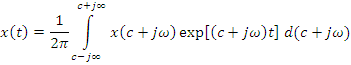
Обозначим ![]()
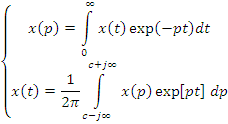
Получено преобразование Лапласа (оригинал + отображение)
Если вместо ![]() подставить
подставить ![]() ,
то получим спектр Ф для Каузальных
функций (т.е.=0 при
,
то получим спектр Ф для Каузальных
функций (т.е.=0 при ![]() ).
).
Итак, спектр
непериодического сигнала ![]() интеграл Ф:
интеграл Ф:
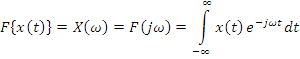
![]() – комплексный амплитудно-частотный
спектр
– комплексный амплитудно-частотный
спектр
![]() – амплитудный спектр
– амплитудный спектр![]()
![]()

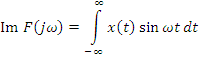
![]()
![]()
Свойства преобразования Ф.
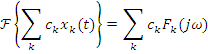
![]()
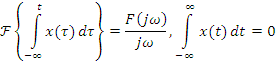
![]()
![]()
-
Преобразование свертки сигналов

![]()
-
Преобразование произведения сигналов
![]()
![]()
-
Спектр мощности сигналов
![]()
![]()
-
Равенство Парсеваля

Спектры некоторых стандартных сигналов
-
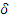 -функции
-функции
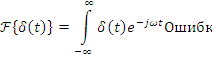
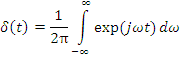
- второе определение
![]() .
.
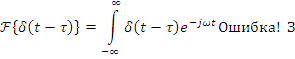
Учитывая свойство
дуальности ![]() .
.
-
Использование
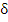 -функции
для нахождения спектров сигналов
-функции
для нахождения спектров сигналов
-
Прямоугольный импульс
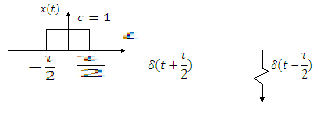

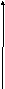
![]()
![]()
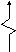
![]()
![]()
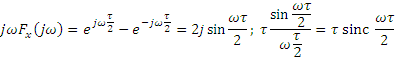
-
Треугольный импульс
![]()
![]()

-
Экспоненциальный импульс
![]()
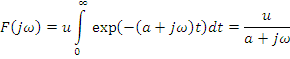
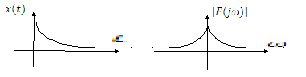
-
Функция Лапласа
![]()
![]()
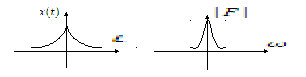
-
Функция Гаусса
![]()
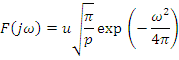
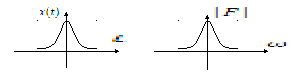
-
Гармонический сигнал
![]()
![]()
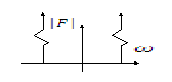
-
Радиоимпульс
![]()
![]()
Спектр сигнала раздваивается с коэффициентом
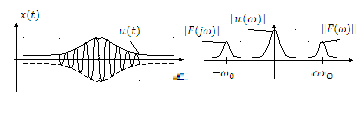
Модуляция сигналов
![]() –
параметры носителя.
–
параметры носителя.
Модулированный сигнал.
![]()
![]() - модулирующая функция, информативный
параметр.
- модулирующая функция, информативный
параметр.
Носители бывают трех типов (постоянный сигнал, гармонический сигнал, импульсный сигнал).

Для типа I – прямая модуляция.
![]() – полезный
системный сигнал (информативный).
– полезный
системный сигнал (информативный).
Для типа II (гармоническая модуляция):
|
|
|
|
|
|
|
|
|
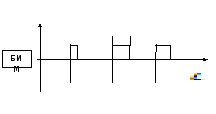
Для типа III (импульсная модуляция):
|
|
|
|
|
|
|
|
|
|
|
Счетно-импульсная модуляция |
|
|
|
Комбинированный тип:
|
|
|
|
|
|
∆-модуляция – такая модуляция, при которой изменяется параметр, а не весь сигнал.
Спектры модулируемых сигналов с гармоническим носителем
Спектр АМ сигнала
![]()
Коэффициент модуляции (глубина модуляции) определяется по формуле:
![]()
Пусть: ![]()
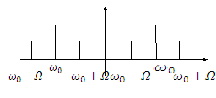
В общем случае спектр АМ сигнала – это произведение двух функций:
![]()
Пусть функция ![]() - спектральная функция
- спектральная функция ![]() .
Спектр произведения есть свертка
спектров.
.
Спектр произведения есть свертка
спектров.
Сделаем некоторые выводы. Пусть:
![]()

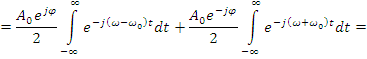
![]()
Т.к.
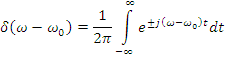
Теперь воспользуемся сделанными выводами. Из свойств интегрального преобразования Фурье:
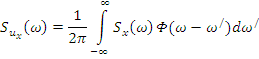
где ![]() – спектральная функция несущей.
– спектральная функция несущей.
![]()
Тогда:
![]()
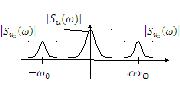
Спектральная
плотность модулированного сигнала
представляет два спектра моделирующего
сигнала, построенных относительно
частот ![]() (т.е. сдвинутых на частоты несущей с
уменьшенной в два раза амплитудой).
(т.е. сдвинутых на частоты несущей с
уменьшенной в два раза амплитудой).
Спектр АИМ сигнала
Пусть ![]() – периодическая последовательность
прямоугольных импульсов,
– периодическая последовательность
прямоугольных импульсов, ![]()

![]()
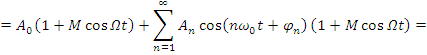
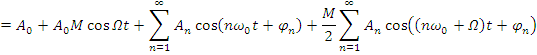

Около каждой гармонической составляющей спектра периодической последовательности импульсов появляются боковые составляющие, соответствующие спектру моделирующей функции.
Корреляционный анализ непрерывного сигнала. Функции корреляции сигналов
Автокорреляционные функции (АКФ)
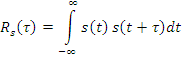
![]() - непрерывная, четная функция, представляет
собой скалярное произведение сигнала
и сдвинутого сигнала.
- непрерывная, четная функция, представляет
собой скалярное произведение сигнала
и сдвинутого сигнала.
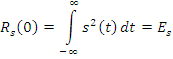
![]() – энергия
сигнала.
– энергия
сигнала.
Приведем доказательство четности:

Четность функции доказана.
По мере увеличения
сдвига ![]() для финитных сигналов, временное
перекрытие уменьшается, и, следовательно,
для финитных сигналов, временное
перекрытие уменьшается, и, следовательно,
![]() и скалярное произведение стремится к
нулю:
и скалярное произведение стремится к
нулю:
![]()
В случае периодичности
сигналов АКФ вычисляется по одному
периоду ![]() с нормированием скалярного произведения
на:
с нормированием скалярного произведения
на:
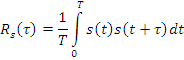
При ![]() средней мощности сигнала на
средней мощности сигнала на ![]() .
.
АКФ для периодических сигналов является периодической функцией. Так, например, пусть:
![]()
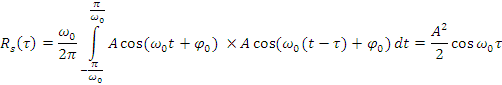
Следовательно, АКФ не зависит от фазы.
Коэффициент автокорреляционного сигнала вычисляется по формуле:
![]()