31. Частотные характеристики экстраполятора нулевого порядка.

Передаточная функция экстраполятора нулевого порядка: ,

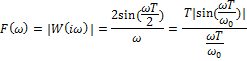
32. Прохождение сигнала во временной и частотной областях через цепочку элементов а-к, цвм, к-а.

Пусть рассматривается дискретная система. ЦВУ выполняет функцию дифференцирования по простейшему алгоритму c задержкой на один такт дискретизации.

Далее приведены осциллограммы сигналов в разных частях дискретной системы и их спектры. Таким образом, на входе импульсного элемента имеется сигнал с ограниченным спектром. Далее после прохождения через импульсный элемент спектр сигнала становится неограниченным в частотной области и периодическим.

Далее после прохода через ЦВУ сигнал изменяем спектр в соответствии с законом дифференцирования продолжая быть неограниченным. После экстраполяции мы видим значительное ослабление копий спектра с увеличением частоты.

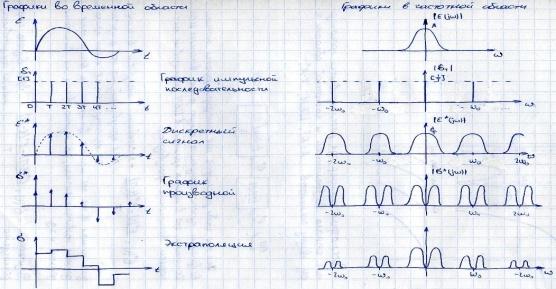
Периодические временные сигналы имеют дискретный частотный спектр. Дискретные временные функции, подвергавшиеся дискретизации, имеют непрерывный дискретный спектр.

33. Передаточная функция и частотные характеристики программы интегрирования, реализованная на цвм методом Эйлера.

Реализация программного интегрирования методом Эйлера: Рекуррентная формула выходного сигнала:

Передаточная функция программы интегрирования:

СММ :

Рассмотрим частотные характеристики:

Рассмотрим ЛАФЧХ системы:

При : , значит в области низких частот ЛАФЧХ такая же, как и у идеального интегратора ;

Однако далее на частотах, примерно больших , характеристика не совпадает с характеристикой идеального дифференциатора, как по амплитуде, так и по сдвигу фаз.

При : ;

34. Передаточная функция и частотные характеристики программы интегрирования, реализованная на ЦВМ по методу трапеций.

y*(t)=y*(t-T) + Tx*(t-T) + (T²/2)x*(t-T)= y*(t-T) + Tx*(t-T) + (T/2)[x*(t-T) – x*(t-2T)]=

=[] = y*(t-T) + (3/2)Tx*(t-T) – (1/2)Tx*(t-2T), y*(s)=y*(s)e^(-sT) + (3/2)Tx*(s) e^(-sT) – (1/2)Tx*(s) e^(-2sT)

Передаточная функция:

Амплитудная характеристика:

_{Частотная характеристика:}

35. Передаточная функция и частотные характеристики программы дифференцирования.

=[переход к половинному аргументу]=

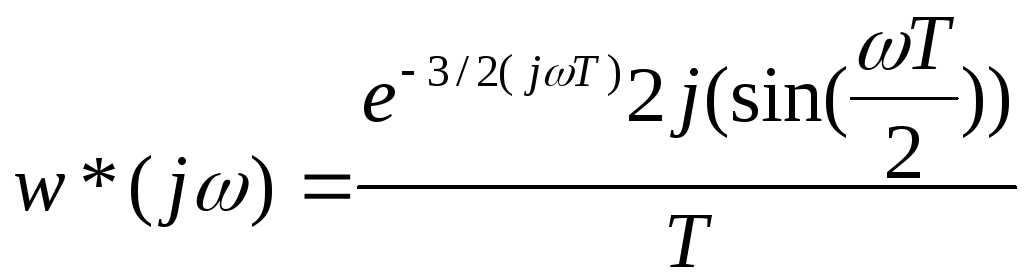
при

36. Передаточная функция и частотные характеристики программы реализации апериодического звена по методу Эйлера.

Соответствующее диффер. уравнение:

Воспользуемся методом Эйлера: y*(t)=y*(t-T) + (T/T_a)(-y*(t-T) + x*(t-T))

Передаточная функция имеет вид:

Структурная схема:

37. Передаточные функции дискретно-непрерывных систем на плоскости W*(s).

y(t)- непрерывный сигнал

y(s)= *(s)·W(s);

преобразование Лапласа дискретного входного сигнала. Будем рассматривать непрерывный выходной сигнал только в тактовые моменты времени, это означает, что мы вводим фиктивный ключ, который замыкается одновременно с первым.

Б)

Теперь рассмотрим дискретно-непрерывную систему: . Опять вводим фиктивный ключ

В)

38. Исследование устойчивости дискретно-непрерывных систем на плоскости s и W*(s).

При построении годографа возникает особенность: известно, что функцияW*(jω) является периодической с периодом 2π/Т, а значит годограф при построении от 0 до бесконечности будет повторяться, поэтому нужно рассматривать годограф на отрезке (0;ω₀), но лучше (-ω₀/2; ω₀/2). Можно построить годограф для положительной оси, а затем отобразить относительно действительной оси. Точно поострить годограф из-за бесконечного числа слагаемых нельзя, поэтому ограничиваются теми, которые дают наибольший вклад. n=0;-1;1 и т.д. Для исследования устойчивости дискретных систем применим критерий Найквиста. Допустим, что разомкнутая дискретная система устойчива, для того, чтобы замкнутая дискретная система была тоже устойчива, годограф не должен охватывать -1. Существенный недостаток состоит в поведении годографа вблизи границы устойчивости ,т.к. отброшенные слагаемые могут повлиять на годограф.

Плоскость s: У передаточной функции разомкнутой системы есть особенность: нули и полюса в силу периодических свойств все те же нули и полюса будут и во всех доп. полосах, критерыий Найквиста работает на участке от 0 до ω₀/2. Значит, рассматриваем те нули и полюса, которые попали в основную полосу справа. Допустим, полюс один, тогда для устойчивости замкнутой дискретной системы нужно, чтобы годограф при изменении Ω от 0 до ω₀/2 охватил -1 в положительном направлении полраза.