§11. Силы упругости

Силы упругости — силы, возникающие при упругой (обратимой) деформации тел.

Закон Гука: сила упругости тела прямо пропорциональна упругой деформации тела.

Закон Гука для винтовой пружины

На рис.11.1 показана винтовая пружина, закрепленная одним концом на опоре в т.А. К незакрепленному концу пружины приложена (рис.11.1а) внешняя сила F_внеш, направленная по оси пружины от опоры. Пружина находится в растянутом состоянии (может быть в сжатом состоянии, если F_внеш будет направлена к опоре).

Внешняя сила F_внеш равна по модулю силе упругости пружины и направлена в противоположную сторону:

(11.1)

Сила упругости пружины приложена к внешнему телу, вызывающему растяжение (или сжатие) пружины.

Сила упругости пружины

(11.2)

где к — жесткость винтовой пружины; r₀ = (r  r₀) — перемещение незакреплённого конца пружины (рис.11.1,в), находящейся в растянутом (может быть в сжатом) состоянии под действием внешней силы; r₀, r — радиус-векторы незакреплённого конца пружины, находящейся в ненагруженном (рис.11.1,а) и нагруженном (рис.11.1,б) состоянии соответственно. Начало координат (см. рис.11.1б) находится в закрепленном на опоре конце пружины — точке А (в общем случае начало координат может находится в любой точке).

Единица жесткости пружины — ньютон на метр: [к] = Н/м.

Удлинение пружины при растяжении (укорочение при сжатии)

(11.3)

где L₀ — длина ненагруженной пружины (см. рис.11.1,а), L — длина нагруженной пружины (см. рис.11.1,б,в).

Модуль силы упругости пружины прямо пропорционален модулю удлинения при растяжении (модулю укорочения при сжатии) пружины:

(11.4)

Если начало координат находится в точке, где находился незакрепленный конец ненагруженной пружины, то

F_упр =  кr. (11.5)

В этом случае проекция силы упругости на ось Ох

(11.6)

где х — координата (называемая также смещением) конца пружины, к которому приложена внешняя сила.

Жесткость системы соединенных пружин

При параллельном соединении пружин (рис.11.2,а) жесткости пружин складываются:

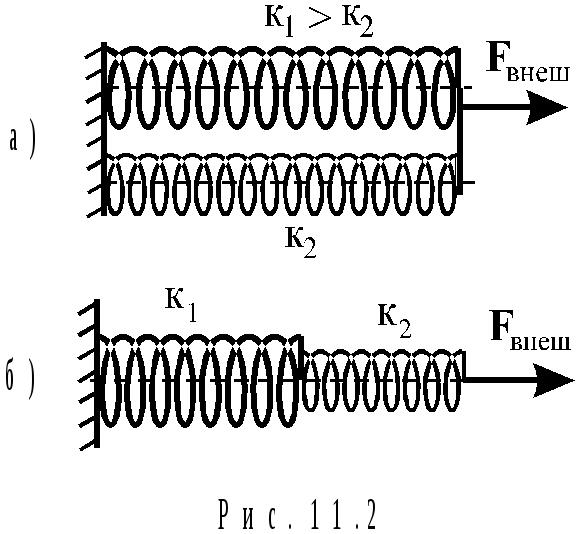
(11.7)

при последовательном соединении пружин (рис.11.2б) складываются величины, обратные жесткостям пружин:

(11.8)

где к_i — жесткость i–й пружины, n — число пружин.

§12. Силы тяготения

Закон всемирного тяготения

Между двумя материальными точками действуют силы тяготения (гравитационные силы), являющиеся силами взаимного притяжения, модули которых прямо пропорциональны произведению их масс и обратно пропорциональны квадрату расстояния между ними. Силы направлены по линии, проходящей через эти материальные точки.

Материальные точки (при использовании в законе всемирного тяготения) — тела, максимальные линейные размеры которых много меньше расстояния между ними: L_i max << r (i = 1,2).

На рис. 12.1 показана материальная точка (м.т.) массой m₁, находящаяся в начале координат, и м.т. массой m₂, которая находится в точке, радиус-вектор которой r.

Сила тяготения F_тяг, действующая со стороны первой материальной точки на вторую:

(12.1)

где G  гравитационная постоянная, равная 6,6710^-11 Нм²/кг², r  расстояние между м.т. (модуль радиус-вектора r).