§7. Движение по окружности

Р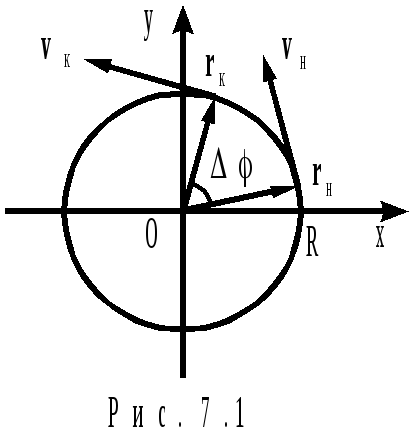авномерное движение материальной точки по окружности — движение, при котором м.т. за любые равные промежутки времени проходит одинаковые по длине дуги окружности.

Является частным случаем равномерного движения материальной точки.

Скорость (линейная скорость) м.т., движущейся по окружности радиуса R (рис.7.1), перпендикулярна радиус-вектору м.т. (начало координат совпадает с центром окружности).

Модуль скорости при равномерном движении материальной точки по окружности

v = const. (7.1)

Модуль угловой скорости (в дальнейшем — угловая скорость)  — СФВ, равная пределу отношения угла поворота  радиус-вектора м.т. к промежутку времени t, за который произошёл этот поворот, при бесконечном уменьшении промежутка времени:

(7.2)

Единица угловой скорости — радиан в секунду: [  ] = рад/с.

Соотношение между модулем линейной скорости и угловой скоростью:

v = R, (7.3)

где R — радиус окружности, являющейся траекторией материальной точки.

При равномерном движении материальной точки по окружности за любые равные промежутки времени углы поворота радиус-вектора м.т. одинаковы.

Угловая скорость при равномерном движении м.т. по окружности — величина, равная отношению угла поворота  радиус-вектора м.т. к промежутку времени t, за который произошёл этот поворот:

(7.4)

Ускорение при таком движении является нормальным (a_ = 0), которое называется также центростремительным:

a_n = a_цc; (7.5)

оно направлено к центру окружности (рис. 7.2) и противоположно радиус-вектору материальной точки:

a_цс = ²r. (7.6)

Модуль центростремительного ускорения прямо пропорционален квадрату угловой скорости:

(7.7)

и квадрату модуля линейной скорости:

(7.8)

Период обращения T — промежуток времени, в течение которого м.т. совершает один оборот (радиус-вектор м.т. поворачивается на угол, равный 2 радиан):

(7.9)

где N — число оборотов м.т. за промежуток времени t.

Путь м.т. за один период равен длине окружности. Модуль линейной скорости может быть найден по формуле:

(7.10)

Частота обращения n — СФВ, равная отношению числа оборотов N, совершенных м.т. за промежуток времени t, к этому промежутку времени:

(7.11)

Единица частоты обращения — обратная секунда:[ n ] = с^1.

Соотношения между угловой скоростью  и частотой n:

 = 2n, (7.12)

периодом Т и частотой n:

(7.13)

периодом Т и угловой скоростью :

. (7.14)

§8. Движение твёрдого тела

Произвольное движение твёрдого тела можно разложить на два вида движения: поступательное и вращательное.

Поступательное движение твердого тела — движение, при котором любая прямая, соединяющая произвольные точки тела, остаётся параллельной своему начальному положению в пространстве. Все точки тела при поступательном движении имеют конгруэнтные (совпадающие при наложении) траектории.

Вращательное движение (вращение) твердого тела — движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой — оси вращения, перпендикулярной плоскостям окружностей.

Угловая скорость вращения твердого тела — угловая скорость любой точки твердого тела (радиус-вектор этой точки лежит в плоскости, перпендикулярной оси вращения, при этом начало его находится в точке, принадлежащей оси вращения).

Плоское движение твердого тела — движение твердого тела, при котором все точки этого тела движутся в плоскостях, параллельных некоторой плоскости.

При плоском движении скорость любой точки твердого тела может быть представлена в виде суммы скорости поступательного движения v_пос некоторой прямой, являющейся осью вращения, и скорости (линейной скорости) вращательного движения данной точки v_вр вокруг этой оси:

v_т = v_пос+ v_вр, (8.1)

Величина угловой скорости вращения одинакова для всех точек твердого тела и не зависит от выбора оси вращения (которая может находиться вне тела).

Примером плоского движения является качение круглого прямого цилиндра по горизонтальной плоскости.

Если точки цилиндра, принадлежащие его оси, имеют постоянную скорость v_сп относительно горизонтальной плоскости (системы отсчёта, связанной с этой плоскостью), то угловая скорость вращения цилиндра (угловая скорость точек цилиндра, не принадлежащих оси вращения)

(8.2)

где R — радиус цилиндра.

Скорость любой точки цилиндра относительно плоскости v_тп может быть найдена из равенства, подобного соотношению (2.22):

v_тп = v_сп + v_тс, (8.3)

где v_тс — скорость точки относительно оси цилиндра (системы отсчета, связанной с этой осью), которая обусловлена вращением цилиндра вокруг своей оси.

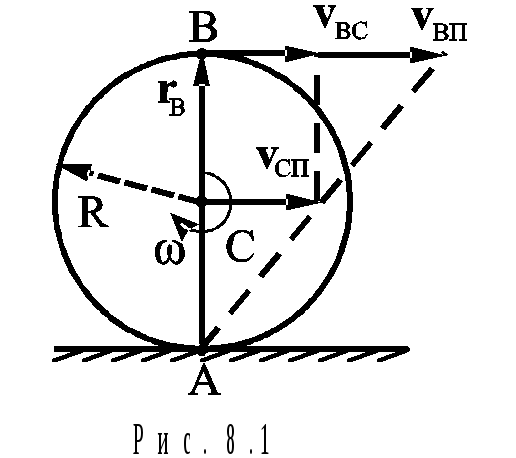
Например, скорость т.В относительно горизонтальной плоскости (на рис.8.1 и рис.8.2 показано основание цилиндра)

v_вп = v_сп + v_вс = 2v_сп, (8.4)

поскольку модуль скорости т.В относительно оси цилиндра v_вс = R = v_сп.

Скорость любой точки цилиндра относительно горизонтальной плоскости можно также определить как линейную скорость при только одном вращательном движении цилиндра с угловой скоростью  относительно мгновенной оси вращения — оси, скорость точек которой относительно этой плоскости равна нулю.

При качении цилиндра без проскальзывания мгновенная ось вращения проходит через точки касания цилиндра с плоскостью (на рис.8.2 показана точка А, принадлежащая этой оси).

Скорость любой точки цилиндра при таком вращении перпендикулярна радиус-вектору r_мт, начало которого находятся на мгновенной оси вращения, а конец  в выбранной точке. Этот радиус-вектор лежит в плоскости, перпендикулярной мгновенной оси вращения. Например, скорость т.P относительно плоскости (рис 8.2) перпендикулярна радиус-вектору r_АР, начало и конец которого находятся в т.А и в т.P соответственно, и направлена по линии, проходящей через т.B, лежащую на одном диаметре с точкой А.

Модуль скорости выбранной точки определяется равенством:

v_рп = r_АР, (8.5)

где r_АР — модуль радиус-вектора выбранной точки Р.

Так, абсолютная величина скорости т.В, модуль радиус-вектора которой r_АВ = 2R (см. рис 8.1), согласно формулы (8.5)

v_ВП = r_АВ = 2R = 2v_СП, (8.6)

что совпадает со значением, найденным по формуле (8.4).

Ускорение любой точки цилиндра относительно горизонтальной плоскости а_тп может быть найдено из равенства, подобного соотношению (3.13):

а_тп = а_тс + а_сп, (8.7)

где а_тс — ускорение точки относительно оси цилиндра, обусловленное вращением цилиндра вокруг своей оси, а_сп — ускорение оси цилиндра относительно горизонтальной плоскости.

При равномерном качении цилиндра а_сп = 0 и ускорение любой точки цилиндра как относительно оси цилиндра, так и относительно горизонтальной плоскости, одно и то же, направлено к оси цилиндра и может быть определено из равенства:

(8.8)

где r_т — вектор, начало и конец которого находятся на оси цилиндра и в выбранной точке соответственно, лежащий в плоскости, перпендикулярной оси вращения.

Модуль ускорения, например т.Р (см. рис.8.2)

(8.9)

поскольку r_Р = R.

Относительно оси цилиндра ускорение а_р точки Р является центростремительным (нормальным) ускорением. Относительно горизонтальной плоскости ускорение точки Р может быть разложено на нормальное а_pn и тангенциальное a_p ускорения (см. рис.8.2), модули которых зависят от угла  между вертикалью и прямой АР:

а_pn = а_рcos, (8.10)

a_p = а_рsin. (8.11)