§3. Ускорение

Среднее ускорение <a> — ВФВ, равная отношению приращения скорости v к промежутку времени t, за который это приращение произошло:

(3.1)

Ускорение (мгновенное) a — ВФВ, равная пределу отношения приращения скорости v к промежутку времени t, за который это приращение произошло, при бесконечном уменьшении промежутка времени:

(3.2)

Единица ускорения — метр на секунду в квадрате: [ a ] = м/с² .

У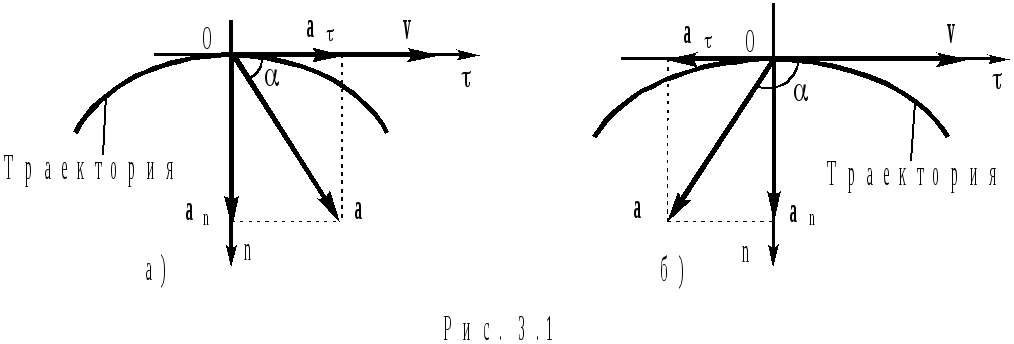скорениеa может быть разложено на взаимно перпендикулярные тангенциальное a_ и нормальное a_n ускорения (показаны на рис.3.1,а и 3.1,б):

a = a_ + a_n. (3.3)

Тангенциальное ускорение a_ характеризует изменение модуля скорости. Оно направлено по касательной к траектории:

a_ = a__ед, (3.4)

где a_ — проекция ускорения на ось О, совпадающую по направлению со скоростью v (см. рис.3.1):

(3.5)

где v — приращение модуля скорости материальной точки; _ед — единичный вектор, направленный по оси О:

_ед (3.6)

Проекция ускорения на ось О может быть больше нуля (рис.3.1a), меньше нуля (рис.3.1б) или равна нулю (например, при равномерном движении м.т. по окружности — см. §7).

Модуль тангенциального ускорения равен модулю проекции ускорения на ось О:

(3.7)

Нормальное ускорение a_n характеризует изменение скорости по направлению. Оно направлено перпендикулярно скорости м.т. к центру кривизны траектории:

a_n = a_nn_ед, (3.8)

a_n — проекция ускорения на ось Оn, направленной к центру кривизны траектории (см. рис.3.1):

(3.9)

где R — радиус кривизны траектории в данной точке, n_ед — единичный вектор, направленный по оси Оn.

Проекция ускорения на ось Оn всегда положительна и равна модулю нормального ускорения:

(3.10)

Д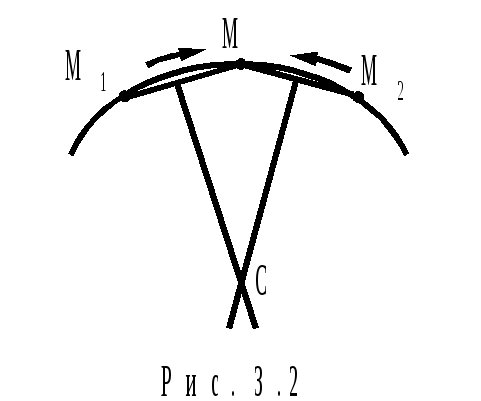ля определения центра и радиуса кривизны траектории в т.М (рис.3.2) на траектории берутся две близкие к т.М точки М₁ и М₂ и через эти три точки проводится окружность. Центром этой окружности (т. С) является точка пересечения перпендикуляров к серединам отрезков ММ₁ и ММ₂. При сближении точек М₁ и М₂ с точкой М, точка С будет стремиться к некоторому предельному положению — точке С₀ (на рис.3.2 не показана).

Точка С₀ называется центром кривизны траектории в т.М, а предельное значение радиуса окружности — радиусом кривизны траектории в т.М.

Модуль ускорения материальной точки

(3.11)

угол между ускорением и скоростью (см. рис.3.1)

(3.12)

Угол между скоростью и ускорением материальной точки может изменяться от нуля до 180(0    180).

Ускорения в различных системах отсчета связаны соотношением:

(3.13)

где a_тк — ускорение материальной точки относительно системы отсчета К (рис.3.3), — ускорение материальной точки относительно системы отсчета,— ускорение системы отсчетаотносительно системы отсчета К.

§4. Равнопеременное движение

Равнопеременное движение — движение, при котором за любые равные промежутки времени (t_i = const) приращения скорости материальной точки одинаковы (v_i = const).

При равнопеременном движении:

ускорение

a = <a> = const, (4.1)

зависимость скорости от времени

v = v_н + at, (4.2)

зависимость радиус-вектора от времени

(4.3)

Равнопеременное прямолинейное движение  равнопеременное движение, при котором приращения скорости коллинеарны скорости материальной точки.

При равнопеременном прямолинейном движении ускорение является тангенциальным, а нормальное ускорение равно нулю:

a = a_, a_n = 0. (4.4)

Согласно равенствам (4.1), (4.2) и (4.3) проекции ускорения (при движении материальной точки в одной плоскости) на оси Ох и Оу

(4.5)

зависимости проекций скорости от времени

(4.6)

зависимости координат от времени

(4.7)

траектория м.т. прямая линия, при этом направления ускорения и скорости м.т. либо совпадают, либо прямо противоположны.

Графики зависимостей a_x(t), v_x(t), x(t) представлены на рис.4.1 а, б, в.

1) если a_x(t) = 0, то v_x(t) = const, x(t) является линейной функцией (участки АВ на графиках этих зависимостей на рис.4.7, а, б, в);

2) если a_x(t) = const, то v_x(t) — линейная функция, x(t) — квадратичная функция (на участках BD и DF графики x(t) — параболы);

3) если в каких-либо точках v_x(t) = 0, то на графике x(t) в этих точках будет либо максимум, либо минимум функции — т.С и т.Е на рис. 4.7, б, в;

4) если на графике v_x(t) нет разрывов (т.В, т.D), то в соответствующих точках на графике x(t) наблюдается плавный переход одной кривой в другую (касательные к этим кривым в точке перехода совпадают).

Равноускоренное прямолинейное движение — равнопеременное прямолинейное движение, при котором модуль скорости увеличивается (v  0).

Направления скорости и ускорения м.т. в начальный и последующие моменты времени совпадают (рис.4.1).

При равноускоренном прямолинейном движении:

модуль скорости

v = v_н + at, (4.8)

путь

(4.9)

График зависимости модуля скорости от времени (при t_н = 0)

v = v_н + at, (4.10)

представлен на рис.4.2.

Путь S за времяtв системе координат vОt при равноускоренном движении равен площади (выраженной в единицах пути) трапеции, ограниченной графиком зависимости v(t), осью времени от начального до конечного моментов времени и отрезками прямых t = t_ни t = t_к.

График квадратичной зависимости пути от времени (S_н= 0 и t_н= 0)

(4.11)

представлен на рис.4.3 (на координатной плоскости SOt пунктиром показано положение вершины параболы, частью которой является график зависимости пути от времени).

При равноускоренном прямолинейном движении:

модуль конечной скорости

(4.12)

среднее значение модуля скорости

(4.13)

Равнозамедленное прямолинейное движение — прямолинейное равнопеременное движение, при котором модуль скорости уменьшается (v  0).

Направления скорости и ускорения м.т. в начальный и последующие моменты времени противоположны (рис.4.4), а само движение существует в промежутке времени:.

При равнозамедленном прямолинейном движении:

модуль скорости

v = v_н – at, (4.14)

путь

(4.15)

Графики зависимости модуля скорости от времени (при t_н = 0)

v(t) = v_н – at (4.16)

и квадратичной зависимости пути от времени (при S_н = 0)

(4.17)

представлены на рис.4.5 и рис.4.6 соответственно.

Путь S за промежуток времени t в системе координат vОt равен площади (выраженной в единицах пути) трапеции (рис.4.5), образованной графиком v(t), осью времени от начального до конечного моментов времени и отрезками прямых t = t_н и t = t_к.

При равнозамедленном прямолинейном движении:

модуль конечной скорости

(при), (4.18)

среднее значение модуля скорости находится по формуле (4.13).