§9. Силы трения

9.1. Тело массой m = 1 кг лежит на горизонтальной плоскости. Коэффициент трения m = 0,1. На тело действует горизонтальная сила F. Определить силу трения для двух случаев: F₁ = 0,5 Н и F₂ = 2 Н.

9.2. Брусок массой m = 2 кг находится на горизонтальной поверхности. Коэффициент трения при скольжении бруска равен m = 0,2. Изобразить графически зависимость силы трения от силы тяги, приложенной к бруску вдоль плоскости скольжения. Явлением застоя пренебречь.

9.3. Доска массой M = 10 кг лежит на гладкой горизонтальной поверхности. Какую горизонтальную силу нужно приложить к доске, чтобы находящийся на ней брусок массой m = 2 кг начал соскальзывать? Коэффициент трения бруска о доску m = 0,1.

9.4. При включении лента транспортера достигает заданной скорости v = 1 м/с за  = 0,5 с. На ленте лежат друг на друге две одинаковые плоские коробки массой m = 500 г. Коэффициент трения коробки о ленту ₁ = 0,5, коэффициент трения коробки о коробку ₂ = 0,1. Определите силу трения, действующую на нижнюю поверхность каждой коробки при разгоне транспортера.

9.5. Используя условие задачи 9.5, определите, на сколько сдвинуться коробки друг относительно друга в процессе разгона транспортера, если они достаточно длинные. На какую максимальную длину сдвинуться коробки?

9.6. Во сколько раз изменится модуль силы трения, действующая на брусок, движущийся по горизонтальной доске, если доску наклонить под углом a = 30 к горизонту?

9.7. Первое тело соскальзывает с горки за время в n = 2 раза большее, чем второе тело. Определите угол наклона  горки к горизонту, если коэффициенты трения между телами и горкой m₁ = 0,2 и m₂ = 0,15.

9.8. Брусок массой m = 1 кг находится на неподвижной наклонной плоскости, составляющей угол a = 45 с горизонтом. С какой минимальной горизонтальной силой нужно действовать на брусок, чтобы он покоился? Коэффициент трения бруска о плоскость m = 0,25.

9.9. Тело толкнули вверх вдоль шероховатой наклонной плоскости. При подъеме величина ускорения тела была равна a₁, при спуске — a₂. Определите угол наклона плоскости к горизонту.

9.10. На тело массойm = 100 кг, лежащее на наклонной плоскости, образующейугол  = 30, действует силаF = 1500 H, направленная вверх под углом β = 30 к наклонной плоскости. Определите ускорение, с которым поднимается тело, если коэффициент трения скольжения m = 0,1.

9.11. При некотором значении коэффициента трения тело массой m = 100 кг равномерно соскальзывает с наклонной плоскости с углом наклона  = 30. Какую силу, параллельную наклонной плоскости, нужно приложить к этому телу, чтобы оно равномерно двигалось вверх по наклонной плоскости?

9.12. Два соприкасающихся бруска соскальзывают с наклонной плоскости. Масса первого бруска m₁ = 2 кг, второго m₂ = 3 кг. Коэффициенты трения между брусками и поверхностью плоскости горкой m₁ = 0,1 и m₂ = 0,3. Угол наклона плоскости к линии горизонта  = 45. Определите силу, с которой бруски давят друг на друга.

9.13. На гранях закреплённой призмы находятся грузы массой m₁ = 1 кг и m₂ = 2 кг, связанные между собой невесомой и нерастяжимой нитью, перекинутой через невесомый блок. Углы наклона граней призмы к линии горизонта  = 30 и β = 60. Коэффициент трения между грузами и поверхностью граней m = 0,1. Определите силу F, с которой блок действует на свою ось. Первоначально грузы покоились.

9.14. Спичечный коробок (₁= 0,3) и ластик (₂= 0,4) кладут на наклонную плоскость с углом наклона а)= 35; б)= 15к горизонту. Массы ластика и коробка одинаковы. На какой предмет действует большая сила трения? Какой из предметов имеет большее ускорение?

9.15. За какое время тело массой m соскользнет с наклонной плоскости высоты h = 6 см с углом наклона  = 35, если по наклонной плоскости с углом наклона  = 30 оно движется вниз равномерно?

9.16.На гладком горизонтальном столе лежит призма массой М с углом наклона , а на ней призма массой m. На меньшую призму действует горизонтальная сила F (см. рисунок), при этом обе призмы движутся как единое целое. Определите силу трения между призмами.

9.17.Призму с углом наклона  = 45 к горизонту двигают с горизонтальным ускорением. При каком минимальном ускорении лежащий на призме брусок начнет двигаться по призме вверх? Коэффициент трения между бруском и призмой  = 0,2.

9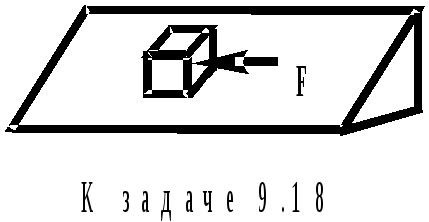.18.Небольшой кубик массой m = 100 г покоится на шероховатой плоскости, наклоненной к горизонту под углом  = 30. Коэффициент трения кубика о плоскость  = 0,8. Определите минимальную горизонтальную силу, лежащую в плоскости склона (см. рисунок), достаточную для того, чтобы кубик начал двигаться?

9.19. Чему должен быть равен минимальный коэффициент трения между шинами и поверхностью наклонной дороги с углом наклона  = 30, чтобы автомобиль мог двигаться по ней вверх с ускорением а = 0,6 м/с²?

9.20. Доска массой М может двигаться без трения по наклонной плоскости с углом  к горизонту. В каком направлении и с каким ускорением должна бежать по доске собака массой m, чтобы доска не соскальзывала с наклонной плоскости? Каким должен быть коэффициент трения к между лапами собаки и доской, чтобы задача имела решение?

9.21. Брусок находится на плоскости, угол наклона которой может изменяться от 0 до 90. Построить график зависимости силы трения бруска о плоскость от угла наклона плоскости к горизонту. Явлением застоя пренебречь.

9.22. Горизонтальная сила F прижимает брусок массы m к неподвижной вертикальной стенке. Коэффициент трения бруска о стенку m = 0,5. При этом брусок движется прямолинейно и равномерно вниз. Чему равно отношение силы F к силе тяжести?

9.23. Горизонтальная сила F прижимает брусок массы m к неподвижной вертикальной стенке, при этом брусок движется вниз с ускорением a = 1м/с². Коэффициент трения бруска о стенку  = 0,5. Чему равно отношение n силы F к силе тяжести?

9.24. Через лёгкий вращающийся без трения блок перекинута невесомая нерастяжимая нить. На одном конце нити привязан груз массой m₁. По другому концу нити может скользить с трением кольцо массой m₂. Каково отношение n = m₁/ m₂, если груз поднимается с ускорением a₁ = 5 м/с², а кольцо опускается с ускорением a₂ = 7 м/с²?

9.25. Какую массу балласта m надо сбросить с равномерно опускающегося аэростата, чтобы он начал равномерно подниматься с той же скоростью? Масса аэростата с балластом М = 1200 кг, подъемная сила аэростата постоянна и равна F = 8000 Н. Силу сопротивления воздуха считать одинаковой при подъеме и при спуске.

9.26. Падающий вертикально вниз мяч массы m = 0,5 кг имеет в некоторый момент времени скорость v₁ = 11 м/с. Через промежуток времени t = 0,2 с скорость шара становится равной v₂ = 12 м/с. Определите модуль силы сопротивления воздуха, действующей на мяч, считая ее постоянной.

9.27.Какова предельно допустимая скорость пешехода при повороте по дуге радиуса R = 40 м при коэффициенте трения между подошвами и дорогой  = 0,1?

9.28. Закругленному участку дороги движутся автомобили на предельно допустимых скоростях (см. рисунок). Как соотносятся времена прохождения закругленного участка по внутреннему и внешнему краю t_a и t_b?